降低EMI的PCB设计指南(一)
- 1.概述
- 2.射频
- 3.连接器与过孔元件
- 4.静态引脚和动态引脚和输入
- 5.基本回路
- 6.差模与共模
tips:资料主要来自网络,仅供学习使用。
1.概述
印刷电路板(PCB)的一般布局准则,基本上都有相对的文件进行了总结,但都比较模糊。一些准则专门适用于微控制器;然而,这些准则是通用的,实际上适用于所有现代CMOS集成电路。后面我们会系统的了解到应用于低噪声、无屏蔽环境中的大多数已知和已发表的布局技术。
随着时间的推移,随着集成电路器件的速度和密度的增加,将需要各种方法来隔离和减少噪声。
2.射频
要讨论的设计准则涉及来自微型计算机的射频噪声。这种噪声是在设备内部产生的,并以许多不同的可能方式耦合出来。噪声始终存在于所有输出端、输入端、电源和接地端。潜在地,微型计算机上的每一个引脚都可能是一个问题。

最大的问题是集成电路(IC)输入/输出(1/0)引脚的噪声。因为PCB上与它们连接的迹线覆盖的区域形成了一个大的天线。这些引脚还连接到内部和外部电缆。IC内时钟切换产生的噪声在静态输出上表现为“小故障”。毛刺是由输出引脚和时钟驱动器的公共阻抗引起的,也就是说,提供每个电源和地的共享引脚。大多数设备的同步性质导致所有的电流开关事件发生在同一时间,使一个大的噪声尖峰包含射频能量。
第二个最重要的噪声源是电源系统,它包括电压调节和在调节器和微型计算机上的旁路电容器。这些电路是系统中所有射频能量的来源,因为它们为IC内部的时钟电路提供开关所需的电流。
第三个噪声源是振荡器电路,振荡器在轨到轨之间摆动。除了基频之外,由于输出缓冲器是数字的它对正弦波进行平方,因此在输出端还会引入谐波。此外,任何由内部操作(如时钟缓冲器)引起的噪声都会出现在输出端。如果晶体和它的槽形电路与PCB上的其他元件和迹线之间保持适当的分离,并且回路区域保持较小,则该噪声源不应该有任何问题。但它已被证明,如果集成电路或无源组件,如主VBatt系列电感器,放置在靠近晶体,晶体的谐波可以耦合和传播。
3.连接器与过孔元件

表面贴装器件(SMD)在处理射频能量方面比引线器件更好,因为它减少了电感和更接近可用的元件位置。后者是可能的,因为减少了物理尺寸的SMD器件。这对于两层电路板设计至关重要,需要噪声控制元件发挥最大效能。一般来说,引线电容器在80 MHz左右都能自谐振(变得比电容更感性)。由于需要控制80 MHz以上的噪声,因此如果设计仅使用通孔组件,则应提出严重的问题。
4.静态引脚和动态引脚和输入
如前所述,在某种程度上,所有线路都有来自处理器的噪声。来自一个引脚的总噪声取决于微型计算机提供给它的噪声量和它在系统中的功能。例如,一个输出引脚具有来自微机电源轨的噪声和来自相邻引脚和基板的电容耦合噪声。如果引脚的功能是系统时钟,那也是噪声。即使引脚在一个或零的水平上是静态的,一个人仍然要与来自芯片内部的噪音作斗争。
在输入模式的I/0引脚的情况下,未使用的输出晶体管的电容将噪声从两个电源轨传输到引脚。噪声量是基于任何连接到引脚的阻抗。阻抗越高,微型计算机发出的噪声就越多。这就是为什么未使用的输入应连接到最低阻抗轨:接地,如果可能的话,通过直接短路。
关于开关输出信号,基本上,只需要担心以大于50kHz的速率进行边沿转换的信号(见图)。如果一个引脚的状态变化率小于每100条指令一次,这是可以接受的,因为开关的贡献可以忽略不计。如果引脚切换,并切换回下一条指令,并保持100条指令的静态,它也是可以接受的,因为它包含相同数量的能量,如在前面的例子。
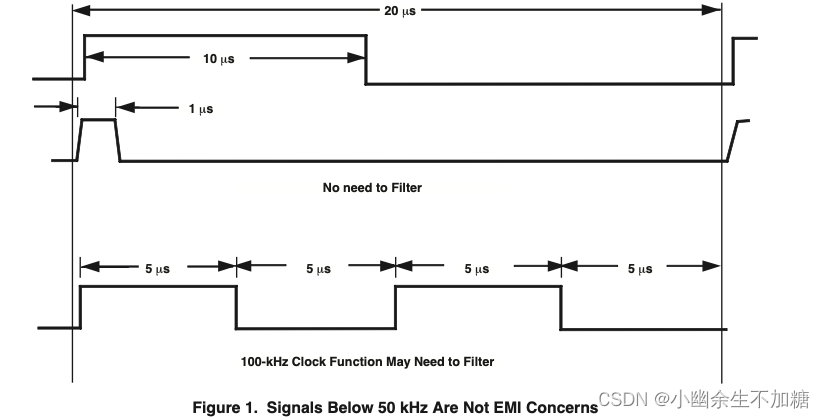
5.基本回路
从微型计算机发送到另一个芯片的每一个边缘转变都是一个电流脉冲。电流脉冲进入接收设备,通过该设备的接地引脚退出,然后通过接地迹线返回到微型计算机的接地引脚(见图)。脉冲并不从接收设备的接地线离开并返回到电池,而是以环路的形式返回到它发出的地方。循环无处不在。任何噪声电压及其相关的电流通过阻抗最低的路径返回到产生噪声的地方。这是一个非常强大的概念因为它允许您通过控制返回路径的形状和阻抗来减轻噪声传播。
环路可以是一个信号及其返回路径,电源和地之间的旁路环路,以及微机内部的有源器件,振荡器晶体及其驱动器,以及从电源或电压调节器到旁路电容器的环路。其他更困难的循环实际上是环境场循环。例如,晶体本身辐射的能量可以耦合到附近的导线。然后,导线中含有试图回到晶体回路的噪声。 这可能涉及到一个非常长的和曲折的路径,它作为另一个天线从晶体噪声。
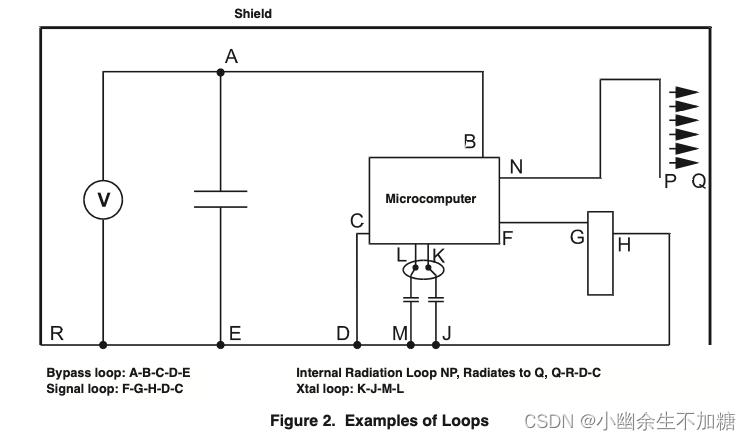
环路和偶极子是天线。它们的辐射效率增加到所需频率的1/4波长(^)。在几何上,这意味着,在环的情况下环的布局面积越大,辐射越强,直到环的一个或两个腿达到1/4波长。在偶极子中,天线的长度越长,辐射越多,直到天线的长度为1/4。
At 1 MHz, 1/4 λ = 75 m. At 300 MHz, 1/4 λ = 25 cm, or about 10 inches。
6.差模与共模
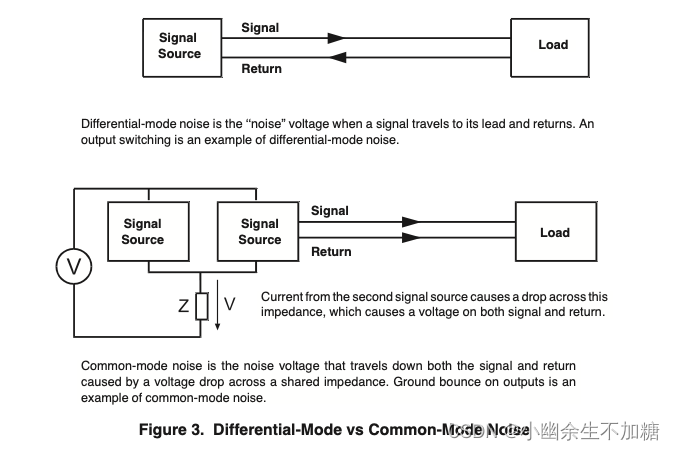
差模噪声是信号沿迹线传输到接收设备,然后沿返回路径返回的噪声(见图)。两根电线之间有个电压差。这是每一个信号为了完成它的工作而必须发出的噪声类型。确保在频率含量(上升和下降时间)和电流幅度方面,没有比完成工作所需的更多噪声。
在共模中,电压同时沿信号线和返回线向下传播。信号和它的返回之间没有差别。电压是由信号和回路共同的阻抗引起的。在大多数不使用外部存储器的基于微型计算机的系统中,公共阻抗噪声是最常见的噪声源。

![[大厂实践] Netflix容器平台内核panic可观察性实践](https://img-blog.csdnimg.cn/img_convert/2a4b58f5c32cbc76b3acfb94b975b9a1.png)


![[算法前沿]--059-大语言模型Fine-tuning踩坑经验之谈](https://img-blog.csdnimg.cn/direct/fea644b86b684eb4a833e45aa5ff4932.png)