检测原理：

       1、导线周围的电磁场

       根据麦克斯韦电磁场理论，交变电流会在周围产生交变的电磁场。智能汽车竞赛使用路径导航的交流电流频率为20kHz，产生的电磁波属于甚低频（VLF）电磁波。甚低频频率范围处于工频和低频电磁破中间，为3kHz～30kHz，波长为100km～10km。如下图所示：

       导线周围的电场和磁场，按照一定规律分布。通过检测相应的电磁场的强度和方向可以反过来获得距离导线的空间位置，这正是我们进行电磁导航的目的。由于赛道导航电线和小车尺寸l 远远小于电磁波的波长λ ，电磁场辐射能量很小（如果天线的长度l 远小于电磁波长，在施加交变电压后，电磁波辐射功率正比于天线长度的四次方），所以能够感应到电磁波的能量非常小。为此，我们将导线周围变化的磁场近似缓变的磁场，按照检测静态磁场的方法获取导线周围的磁场分布，从而进行位置检测。

       由毕奥-萨伐尔定律知：通有稳恒电流I 长度为L 的直导线周围会产生磁场，距离导线距离为r 处P 点的磁感应强度为：

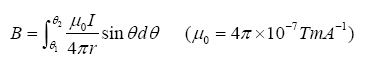
（1）

由此得:

对于无限长直电流来说，上式中θ1 = 0 ，θ2=π ，则有

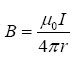
       在上面示意图中，感应磁场的分布是以导线为轴的一系列的同心圆。圆上的磁场强度大小相同，并随着距离导线的半径r 增加成反比下降。

2、磁场检测方法：

       通电导线周围的磁场是一个矢量场，场的分布如图四所示。如果在通电直导线两边的周围竖直放置两个轴线相互垂直并位于与导线相垂直平面内的线圈，则可以感应磁场向量的两个垂直分量，进而可以获得磁场的强度和方向。                                         

       导线中的电流按一定规律变化时，导线周围的磁场也将发生变化，则线圈中将感应出一定的电动势。 根据法拉第定律，线圈磁场传感器的内部感应电压E 与磁场B(t) 、电磁线圈的圈数N 、截面积A 的关系有：

        

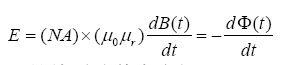
       感应电动势的方向可以用楞次定律来确定。

       由于本设计中导线中通过的电流频率较低，为20kHz，且线圈较小，令线圈中心到导线的距离为 r ，认为小范围内磁场分布是均匀的。再根据图3 所示的导线周围磁场分布规律，则线圈中感应电动势可近似为：

        

（2）

       即线圈中感应电动势的大小正比于电流的变化率，反比于线圈中心到导线的距离。其中常量K 为与线圈摆放方法、线圈面积和一些物理常量有关的一个量，具体的感应电动势常量须实际测定来确定。

3、双水平线圈检测方案

       不同的线圈轴线摆放方向，可以感应不同的磁场分量。我们先讨论一种最简单的线圈设置方案：双水平线圈检测方案。在车模前上方水平方向固定两个相距L 的线圈，两个线圈的轴线为水平，高度为h ，如下图所示：

       为了讨论方便，我们在跑道上建立如下的坐标系，假设沿着跑道前进的方向为z轴，垂直跑道往上为y轴，在跑道平面内垂直于跑到中心线为x轴。xyz轴满足右手方向。

      假设在车模前方安装两个水平的线圈。这两个线圈的间隔为L，线圈的高度为h，参见下图5所示。左边的线圈的坐标为（x,h,z），右边的线圈的位置(x-L,h,z)。由于磁场分布是以z轴为中心的同心圆，所以在计算磁场强度的时候我们仅仅考虑坐标(x,y)。

       由于线圈的轴线是水平的，所以感应电动势反映了磁场的水平分量。根据公式（2）可以知道感应电动势大小。

假设h=5cm, x∈(−15,+15)cm，计算感应电动势

随着线圈水平位置x 的变化取值，如下图所示：

如果只使用一个线圈，感应电动势E 是位置x 的偶函数，只能够反映到水平位置的绝对值x 的大小，无法分辨左右。为此，我们可以使用相距长度为L 的两个感应线圈，计算两个线圈感应电动势的差值：

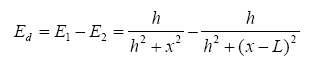
下面假设L = 30cm ，计算两个线圈电动势差值d E 如下图所示：

从上图可以看出，当左边线圈的位置x = 15cm的时候，此时两个线圈的中心恰好处于跑道中央，感应电动势差值d E 为0。当线圈往左偏移， x ∈ (15,30) ，感应电动势差值小于零；反之，当线圈往右偏移， x ∈ (0,15) ，感应电动势大于零。因此在位0∼30cm 之间，电动势差值d E 与位移x 是一个单调函数。可以使用这个量对于小车转向进行负反馈控制，从而保证两个线圈中心位置跟踪赛道的中心线。通过改变线圈高度h ,线圈之间距离L 可以调整位置检测范围以及感应电动势的大小。