机器学习复习（8）—

机器学习复习（8）——逻辑回归

逻辑函数（Logistic Function）

逻辑回归模型的假设函数

从逻辑回归模型转换到最大似然函数过程

最大似然函数方法

梯度下降

逻辑函数（Logistic Function）

首先，逻辑函数，也称为Sigmoid函数，是一个常见的S形函数。其数学表达式为：

$g(z)=\frac1{1+e^{-z}}$

这个函数的特点是，其输出值总是在0和1之间。这个性质使得Sigmoid函数非常适合用来进行二分类，在机器学习中，它可以将任意实数映射到(0, 1)区间，用来表示某个事件发生的概率。例如，在逻辑回归模型中，我们可以用它来预测一个实例属于某个类别的概率。

def sigmoid(z):return 1 / (1 + np.exp(-z))

可视化：

nums = np.arange(-10, 10, step=1)fig, ax = plt.subplots(figsize=(12,8))
ax.plot(nums, sigmoid(nums), 'r')
plt.show()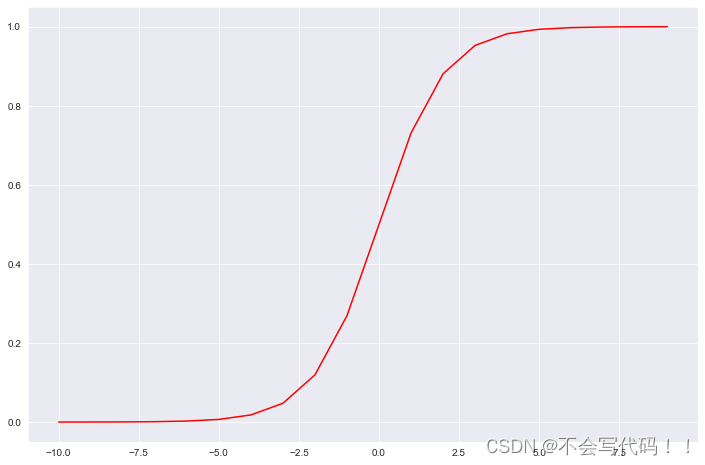

逻辑回归模型的假设函数

逻辑回归模型的假设函数将输入特征X和参数θ的线性组合通过逻辑函数转换为一个概率值，其公式为：

$h_\theta(x)=\frac1{1+e^{-\theta^TX}}$

这里，θ^T X是参数θ和输入特征X的点积，它将多个输入特征线性组合成一个实数值，然后通过逻辑函数映射到(0, 1)区间。这个映射的结果可以被解释为在给定输入特征X的条件下，预测结果为正类的概率。

逻辑回归模型通过优化参数θ来最大化观测数据的似然函数，从而找到最佳的决策边界，以区分不同的类别。在实际应用中，逻辑回归是一个非常强大且广泛使用的分类算法，特别是在二分类问题中。

从逻辑回归模型转换到最大似然函数过程

逻辑回归模型的假设函数定义为：

$h_\theta(x)=g(\theta^Tx)=\frac{1}{1+e^{-\theta^Tx}}$

为了找到最佳的参数θ，我们使用最大似然估计。对于二分类问题，给定的数据集 $D=\{(x^{(i)},y^{(i)})\}_{i=1}^{m}$ ，其中 $y^{(i)}\in\{0,1\}$ ，，我们可以写出似然函数：

$L(\theta)=P(y|X;\theta)=\prod_{i=1}^m(h_\theta(x^{(i)}))^{y^{(i)}}(1-h_\theta(x^{(i)}))^{1-y^{(i)}}$

这个似然函数表示了，在给定参数θ和输入X的条件下，观察到当前数据集y的概率。最大化这个似然函数等价于最大化观测数据在当前模型参数下出现的概率。

为了便于计算，通常对似然函数取对数，得到对数似然函数：

$\log L(\theta)=\sum_{i=1}^m[y^{(i)}\log h_\theta(x^{(i)})+(1-y^{(i)})\log(1-h_\theta(x^{(i)}))]$

最大化对数似然函数相对简单，因为对数函数是单调的，且对数似然函数是关于θ的凸函数，容易通过梯度下降等优化算法找到全局最优解。

在机器学习中，我们通常通过最小化损失函数（而不是最大化似然函数）来训练模型。因此，我们将最大化对数似然问题转化为最小化损失函数问题。损失函数是对数似然函数的负值，平均化到每个样本上，即：

这就是逻辑回归中使用的损失函数，也称为对数损失或交叉熵损失。通过最小化这个损失函数，我们可以找到最佳的模型参数θ，使模型对训练数据的拟合程度最高，即最可能产生观测数据的参数。

最大似然函数方法

由于乘除法不太好优化计算，通常通过对数的方法进行优化求解，损失函数如下：

$\begin{aligned}J(\theta)=-\frac{1}{m}\sum_{i=1}^{m}[y^{(i)}\log(h_{\theta}(x^{(i)}))+(1-y^{(i)})\log(1-h_{\theta}(x^{(i)}))]\end{aligned}$

def cost(theta, X, y):theta = np.matrix(theta)X = np.matrix(X)y = np.matrix(y)first = np.multiply(-y, np.log(sigmoid(X * theta.T)))second = np.multiply((1 - y), np.log(1 - sigmoid(X * theta.T)))return np.sum(first - second) / (len(X))

梯度下降

实际上这里只计算量梯度，并没有下降

def gradient(theta, X, y):theta = np.matrix(theta)X = np.matrix(X)y = np.matrix(y)parameters = int(theta.ravel().shape[1])grad = np.zeros(parameters)error = sigmoid(X * theta.T) - yfor i in range(parameters):term = np.multiply(error, X[:,i])grad[i] = np.sum(term) / len(X)return grad

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/255777.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！