P1678 烦恼的高考志愿

写完后发现题解里面用的是优先队列或者二分什么的，其实这个题可以贪心，我们把学校的分数线和学生的成绩分别进行排序，然后从前往后遍历，每次比较当前学校的分数与学生成绩的差距和下一个学校的分数与学生成绩之间的差距，如果前面那个小就把他加进sum，遍历完所有学生即可得出答案，记得有一点就是遍历下一个学生时，学校不往后推，不然结果会错误

#include<bits/stdc++.h>
using namespace std;
int a[100009],b[100009];
long long sum=0;
int main(){int n,m;scanf("%d %d",&n,&m);for(int i=1;i<=n;i++){scanf("%d",&a[i]);}for(int j=1;j<=m;j++){scanf("%d",&b[j]);}sort(a+1,a+1+n);sort(b+1,b+1+m);a[n+1]=100000000;int flag=1;for(int i=1;i<=n;i++){if(flag==m+1)break;if(abs(a[i]-b[flag])<abs(a[i+1]-b[flag])){//	printf("%d %d\n",a[i],b[flag]);sum+=abs(a[i]-b[flag]);i--;flag++;}}printf("%lld",sum);	return 0;
}

P1364 医院设置

每个医院都可以看成是一个节点，本题需要创造一个树，接着以每一个节点为起点遍历，用dfs对树进行遍历，记录每次结果的最小值，最后得到答案dfs，注意遍历顺序

#include<bits/stdc++.h>
using namespace std;
struct node{int human;int left;int right;int father;
};
node tree[1000];
int vis[105],n,sum,ans=INT_MAX;
void dfs(int step,int pos){sum+=step*tree[pos].human;int fa=tree[pos].father,left=tree[pos].left,right=tree[pos].right;if(fa&&!vis[fa]){vis[fa]=1;dfs(step+1,fa);}if(left&&!vis[left]){vis[left]=1;dfs(step+1,left);}if(right&&!vis[right]){vis[right]=1;dfs(step+1,right);}
}
int main(){scanf("%d",&n);for(int i=1;i<=n;i++){scanf("%d %d %d",&tree[i].human,&tree[i].left,&tree[i].right);tree[tree[i].left].father=i;tree[tree[i].right].father=i;}for(int i=1;i<=n;i++){sum=0;memset(vis,0,sizeof(vis));vis[i]=1;dfs(0,i);ans=min(ans,sum);}printf("%d",ans);return 0;
}

P1258 小车问题

昨天提到的小车问题的正解是二分，但是我图简单用的数学方法

首先，每个人都要做一次车，而且两个人要同时到达，这样才能使总时间最短。

那么，我们设起点为A，终点为B，小车先带甲开到C点后甲下车走到B点，同时小车掉头与已经走到D点的乙相向而行，相遇于点E，最后小车带乙向B开去，和甲同时到达。

现在设AC=S

则：

#include<bits/stdc++.h>
using namespace std;
int main()
{double s,s1,s2,v1,v2,t1,t2,p;double a,b;scanf("%lf%lf%lf",&s,&v1,&v2);s1=0;s2=s;do{p=(s1+s2)/2.0;a=p/v2;b=(p-a*v1)/(v1+v2);t1=a+(s-p)/v1;t2=a+b+(s-(a+b)*v1)/v2;if(t1<t2)s2=p;elses1=p;}while(fabs(t1-t2)>1e-8);printf("%.6lf",t1);return 0;
}

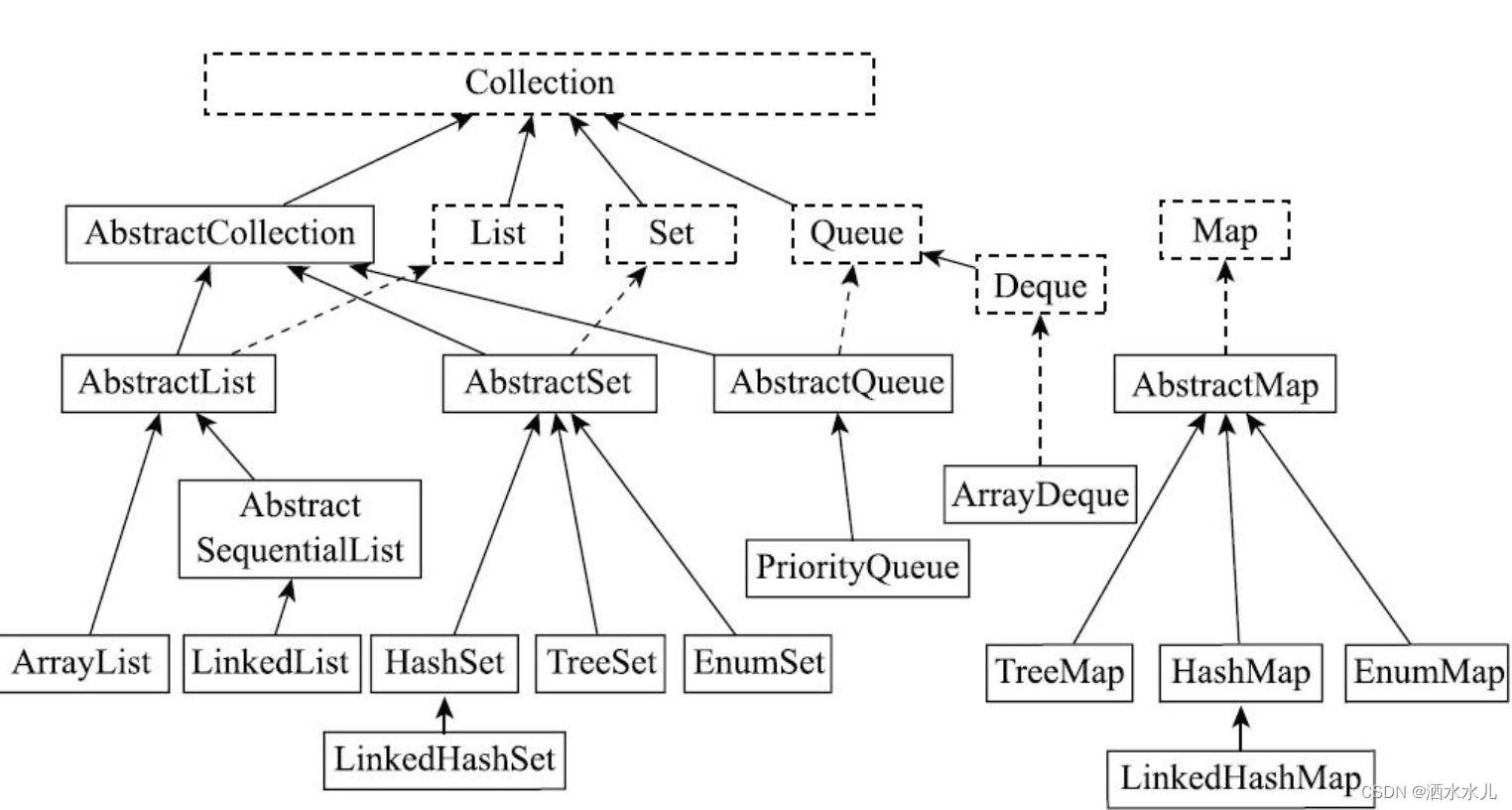
一、二叉树
二叉树（Binary Tree）是一种重要的树状数据结构，它由节点构成，每个节点最多有两个子节点：一个左子节点和一个右子节点。这种结构使得二叉树在计算机科学和编程中具有广泛的应用。

1.1 二叉树的基本特性：
根节点：二叉树的顶部节点称为根节点，它是树的起点。
子树：树中的任何节点都可以作为根节点形成子树。
父节点和子节点：节点可以有零、一个或两个子节点。父节点指向子节点。
叶子节点：没有子节点的节点称为叶子节点。
深度：从根节点到某个节点的路径长度称为深度。根节点深度为0。
高度：树中最深节点的深度称为树的高度。
层次：节点的深度加1就是该节点所在的层次。
1.2 二叉树的常见类型：
二叉搜索树（Binary Search Tree，BST）：一种有序二叉树，左子树上的节点值小于根节点，右子树上的节点值大于根节点，这个性质使得二叉搜索树用于快速查找、插入和删除操作。
平衡二叉树：一种特殊的二叉搜索树，保持树的左右子树高度差不超过1，以保持查找操作的高效性能。常见的平衡二叉树包括AVL树和红黑树。
二叉堆（Binary Heap）：一种特殊的二叉树结构，通常用于实现堆排序和优先队列。有最大堆和最小堆两种类型。
1.3 二叉树的遍历方式：
前序遍历（Preorder Traversal）：先访问根节点，然后依次遍历左子树和右子树。
中序遍历（Inorder Traversal）：先遍历左子树，然后访问根节点，最后遍历右子树。对于二叉搜索树，中序遍历的结果是有序的。
后序遍历（Postorder Traversal）：先遍历左子树，然后遍历右子树，最后访问根节点。
层次遍历（Level Order Traversal）：按层次从上到下，从左到右遍历树的节点。

二、图的基本概念
图（Graph）是一种抽象数据结构，用于表示多个对象之间的关系。图是计算机科学中非常重要的数据结构，用于解决许多实际问题。以下是图的基本概念：

节点（Node 或 Vertex）：图中的基本元素，通常表示一个实体或对象。节点可以有不同的属性和类型，具体取决于应用。节点可以包含有关实体的信息，如名称、权重等。
边（Edge 或 Arc）：图中连接两个节点的线，表示节点之间的关系。边可以是有向的（从一个节点到另一个节点）或无向的（没有方向）。通常，边可能具有权重，用于表示关系的强度或成本。
顶点数（Vertex Count）：图中节点的总数。
边数（Edge Count）：图中边的总数。
路径（Path）：在图中，路径是一系列相邻的节点，它们通过边相连。路径的长度可以通过经过的边数或权重来度量。
有向图（Directed Graph）：也称为有向图，图中的边具有方向。在有向图中，从一个节点到另一个节点的边是单向的。
无向图（Undirected Graph）：在无向图中，图中的边没有方向，可以双向移动。
环（Cycle）：在图中，如果一条路径可以回到起始节点，形成一个闭合的环，那么该路径被称为环。
连通性（Connectivity）：一个图或图中的一部分被称为连通的，如果从任何一个节点到另一个节点都存在路径。
度数（Degree）：节点的度数是与该节点相连的边的数量。在有向图中，分为入度（In-Degree）和出度（Out-Degree）。
子图（Subgraph）：一个图的子集，包括一些节点和连接这些节点的边。
稀疏图和稠密图：稀疏图是具有相对较少边的图，而稠密图具有相对较多的边。
图是一种非常通用的数据结构，它在许多领域中都有广泛的应用，包括网络分析、社交网络、路线规划、数据库系统、编译器设计、图像处理等。不同类型的图和图算法被用于不同的问题，如最短路径问题、网络流问题、最小生成树问题等。了解这些基本概念是理解和使用图的关键。

三、常见图算法
图算法是解决图数据结构中的各种问题的算法。以下是一些常见的图算法，以及它们的简要介绍和C#、Java的代码示例：

3.1 深度优先搜索（DFS）：
算法介绍：DFS 用于遍历图，从一个起始节点开始，沿着一条路径尽可能深入，直到无法再继续。然后，回溯到上一个节点，继续深入其他路径，直到所有节点都被访问。
应用：查找连通组件、拓扑排序、解决迷宫问题等。