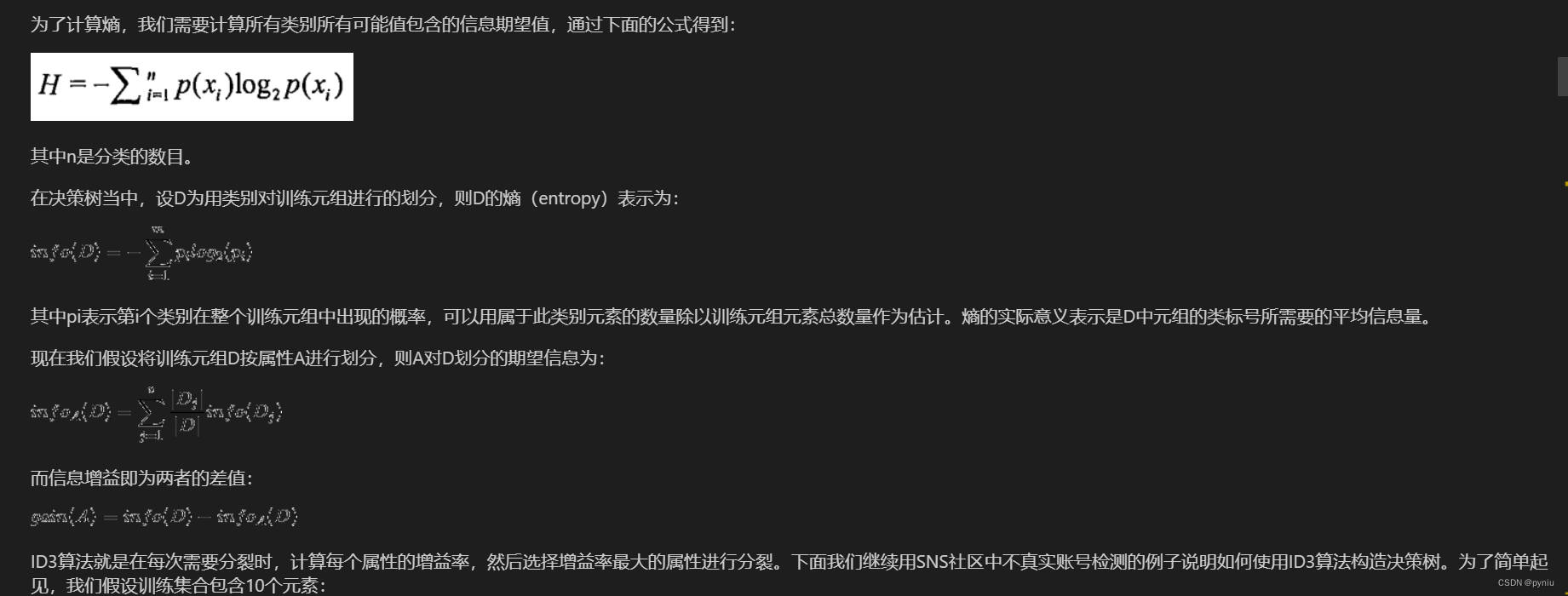
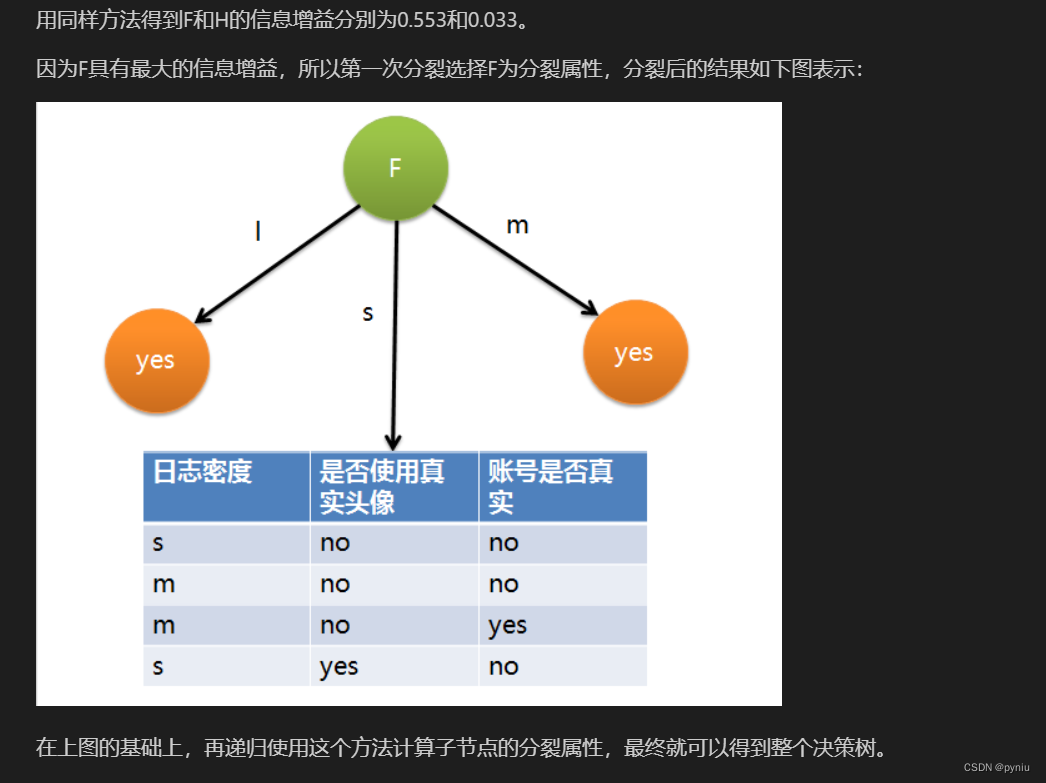
这是前期准备

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
#ID3算法
#每个特征的信息熵
# target : 账号是否真实，共2种情况
#    yes  7个   p=0.7
#    no   3个   p=0.3
info_D=-(0.7*np.log2(0.7)+0.3*np.log2(0.3))
info_D
#日志密度L
# 日志密度 3种结果
#   s   3个  0.3   1yes,2no
#   m   4个  0.4   3yes,1no
#   l   3个  0.3   3yes,0no
info_L_D = 0.3 * ( - ( (1/3) * np.log2(1/3)  + (2/3) * np.log2(2/3) ) ) \+ 0.4 * ( - ( (3/4) * np.log2(3/4)  + (1/4) * np.log2(1/4) ) ) # + 0.3 * ( - ( (3/3) * np.log2(3/3)  + (0/3) * np.log2(0/3) ) ) info_L_D
#而信息增益即为两者的差值
gain_L = info_D - info_L_D
gain_L
# 好友密度 3种结果
#   s   4个  0.4   1yes,3no
#   m   4个  0.4   4yes,0no
#   l   2个  0.2   2yes,0noinfo_F_D = 0.4 * ( - ( (1/4) * np.log2(1/4)  + (3/4) * np.log2(3/4) ) ) info_F_D
gain_F = info_D - info_F_D
gain_F
# 是否使用真实头像 2种结果
#   yes   5个  0.5   4yes,1no
#   no    5个  0.5   3yes,2noinfo_H_D = 0.5 * ( - ( (4/5) * np.log2(4/5)  + (1/5) * np.log2(1/5) ) )  \+ 0.5 * ( - ( (3/5) * np.log2(3/5)  + (2/5) * np.log2(2/5) ) ) info_H_D
gain_H = info_D - info_H_D
gain_H
# ID3算法
#   信息增益： gain_F > gain_L > gain_H
#                0.55 > 0.28   > 0.03# 优先分裂：好友密度
# 如果有类似ID的特征（每一个值都不一样）
#    ID有10种结果
#       1     有1个   0.1    1yes或1no
#       2     有1个   0.1    1yes或1no
#       3     有1个   0.1    1yes或1no
#       4     有1个   0.1    1yes或1no
#       5     有1个   0.1    1yes或1no
#       6     有1个   0.1    1yes或1no
#       7     有1个   0.1    1yes或1no
#       8     有1个   0.1    1yes或1no
#       9     有1个   0.1    1yes或1no
#      10     有1个   0.1    1yes或1no# info_ID_D = 0.1 * ( - ( (0/1) * np.log2(0/1)  + (1/1) * np.log2(1/1) ) )   * 10
info_ID_D  = 0# ID的信息增益
gain_ID = info_D - info_ID_D
gain_ID
### C4.5算法
# 解决的主要问题是： ID3算法中出现的ID属性的问题
# 单独计算每个特征的信息熵
# 信息增益率  
#  信息增益率 = 信息增益 / 每个特征单独的信息熵# 日志密度L
#   s   3个  0.3   
#   m   4个  0.4   
#   l   3个  0.3  info_L = - ( 0.3 * np.log2(0.3)  + 0.4 * np.log2(0.4) + 0.3 * np.log2(0.3) )
info_Lgain_L / info_L
# 好友密度F
#   s   4个  0.4 
#   m   4个  0.4   
#   l   2个  0.2  info_F = - ( 0.4 * np.log2(0.4)  + 0.4 * np.log2(0.4) + 0.2 * np.log2(0.2) )
info_Fgain_F / info_F
# 是否使用真实头像H
#   yes   5个  0.5
#   no    5个  0.5   info_H = - ( 0.5 * np.log2(0.5)  + 0.5 * np.log2(0.5)  )
info_Hgain_H / info_H
# ID
#   1    1个  0.1
#   2    1个  0.1   
#   ... 
#  10    1个  0.1   info_ID = - ( 0.1 * np.log2(0.1)  * 10 )
info_IDgain_ID / info_ID
#  好友密度最大 0.36  ###  CART算法
#gini_D = 1 - sum( p(x)**2 )
#gini : 基尼， 基尼系数，作用类似信息熵
%timeit np.log2(1000000)
%timeit 1000000**2 
# target : 账号是否真实，共2种情况
#    yes  7个   p=0.7
#    no   3个   p=0.3gini_D = 1 - ( 0.7**2 + 0.3**2 )
gini_D
# 日志密度 3种结果
#   s   3个  0.3   1yes,2no
#   m   4个  0.4   3yes,1no
#   l   3个  0.3   3yes,0nogini_L_D = 0.3 * ( 1 - ((1/3)**2 + (2/3)**2)) \+ 0.4 * ( 1 - ((1/4)**2 + (3/4)**2)) \+ 0.3 * ( 1 - ((3/3)**2 + (0/3)**2))gini_L_D
gini_D - gini_L_D
# 好友密度 3种结果
#   s   4个  0.4   1yes,3no
#   m   4个  0.4   4yes,0no
#   l   2个  0.2   2yes,0nogini_F_D = 0.4 * ( 1 - ((1/4)**2 + (3/4)**2) ) gini_F_D
gini_D - gini_F_D
# 是否使用真实头像 2种结果
#   yes   5个  0.5   4yes,1no
#   no    5个  0.5   3yes,2nogini_H_D = 0.5 * ( 1 - ( (4/5) **2  + (1/5) **2 ) )  \+ 0.5 * ( 1 - ( (3/5) **2  + (2/5) **2 ) ) gini_H_D
gini_D - gini_H_D

#决策树代码
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
data, target = load_iris(return_X_y=True)
data.shape, target.shape
#criterion='gini', gini系数， 默认使用CART算法，一般使用默认值
#- splitter='best',  分割方式， 默认是best，最好的分割方式
#- max_depth=None,   树的最大深度，数据量少的情况下不设置，默认没有限制深度，
#    -  数据量大的情况下需要设置，防止过拟合
#- min_samples_split=2, 最小分裂的样本数，数据量少的情况下不设置，默认是2
#    -  数据量大的话，可以增加该值
#- min_samples_leaf=1,  叶子节点所需要的最少样本数，
#   -  如果叶子节点上的样本数小于该值，则会被剪枝(兄弟节点一般也会被剪枝)
#    -  数据量不大的情况下，一般不设置，
#   -   如果数据量比较大（上万）的时候考虑增加该值
tree=DecisionTreeClassifier(max_depth=2)
tree=DecesionTreeClassifier(min_samples_split=4,min_samples_leas=4)
tree.fit(data).score(data,target)