一、多目标规划简介

多目标规划的本质是“既要XXX又要XXX”，而不论是线性规划还是非线性规划都是一个目标函数，例如工业生产产品，追求最大化利润等。但是多目标规划存在多个目标，可以转化出多个目标函数，故难点在同时满足所有目标。由此思路为：

• 需要衡量每个目标的完成情况
• 如果三个目标有一定冲突，要在主观上区分三个目标的重要性
• 使得整体的完成情况尽量好

二、适用赛题

生产规划等问题，如“使XXX最少/多/利润最大”“尽可能XXX”“尽量XXX”等。

三、模型流程

四、流程分析

1.前提假设

老生常谈，这里就不讲了。

2.提取目标

既然是多目标规划，自然就不止一个目标，将所有的目标提取出来。

3.翻译

①正负偏差变量

正负偏差变量是用来衡量每个目标的完成情况

• 设fi(i = 1, ..., l) 为第i个目标函数的实际值，di表示fi的目标值
• 正偏差变量di1 = max{fi - di, 0}为实际值超过目标值的部分
• 负偏差变量di2 = -min{fi - di, 0}为实际值未达到目标值的部分

通过正负偏差变量可以将目标函数转化为用正负偏差变量表示

例如有如下的目标函数

函数1： x1 - x2 ≤ 0

函数2： 8x1 + 10x2 ≥ 56

则可以转化为

min d11（最小的正偏差变量）解释：函数1表明希望x1尽量比x2小，小多少无所谓，但是尽量别让x1大于x2，所以我们要求最小的正偏差变量

min d22（最小的负偏差变量）解释：函数2表明希望左边式子尽量大于等于56，大多少无所谓，但是尽量别小于56，所以要求最小的负偏差变量

②绝对约束和目标约束

• 绝对约束是模型中自带的约束条件，必须满足，否则是不可行解
• 目标约束是模型中对不等式右端追求的值允许有偏差
• “尽量”“尽可能”就是允许有偏差，这个条件达不达到都行，这样就无法有一个准确的约束式子
• 利用正负偏差变量，可以获得准确的等式约束条件

如上面的函数1

有x1 - x2 + d12 - d11 = 0

函数2有 8x1 + 10x2 + d22 - d21 = 56

这样就有了等式约束条件，其实就是实际值加上未达到的部分、减去超过的部分，就等于目标值。

③优先因子

多个目标可能难以同时满足，到底哪个更重要？这个可以根据文献或题目要求确定。

然后设最重要目标的优先因子是P1，第二重要是P2，后面以此类推。

注意：不同的求解方法下，优先因子的作用是不同的。在序贯算法中，优先因子只是用来区分目标的相对重要性，不需要其具体值。而在线性加权法中，需要确定具体数值（该方法过于简单，适用性小，不建议使用）。

这里通过一个例题操作示范

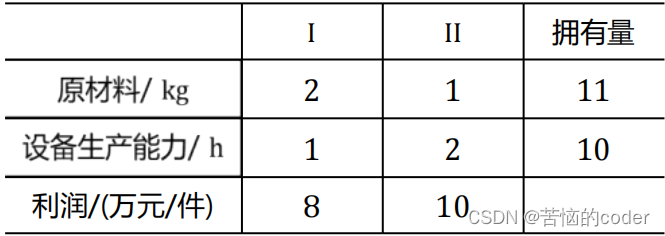
按照前面所讲，将3个目标转化为数学语言

别忘了还有绝对约束：2x1 + x2 ≤ 11，因为生产材料有限。

从而建立模型

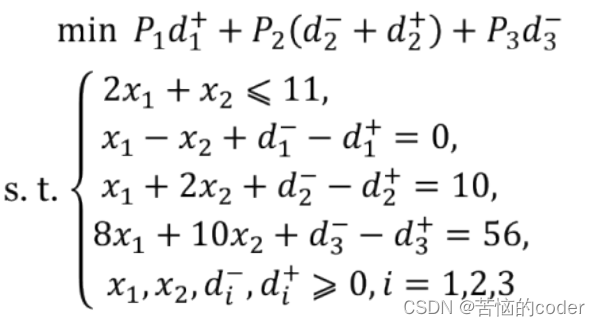
4.划分

根据优先因子的先后次序，将问题分解成单目标规划。三个目标，每个目标都可视为单目标的线性规划。

5.序贯算法求解

序贯算法是一种常用解法

• 根据模型中各个目标的优先级（优先因子），确定各目标的求解次序
• 求第一级单目标规划的最优值记为f1*
• 以第一级单目标等于最优值f1*为新的约束，求第二级目标的最优值f2*
• 依次递推，直到所有目标都求完，或不存在可行解为止

推荐使用优化变量、优化问题来求解。