树状数组算法原理

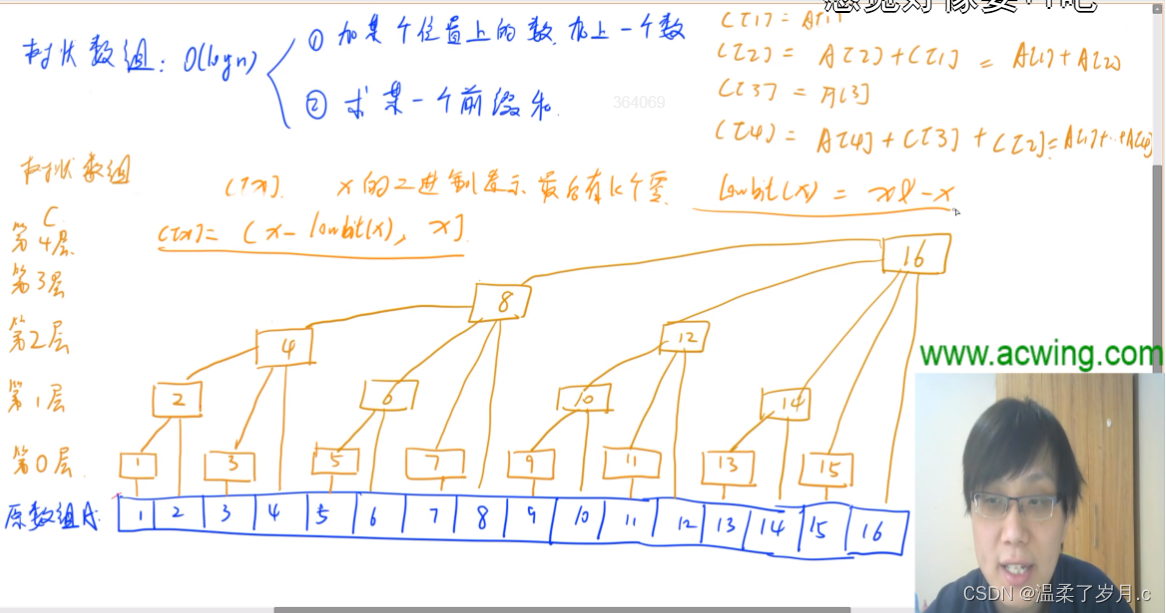
这里注意：C[x]的含义和lowbit()函数

基本操作

最基本的操作主要是两种
1.改变某个数（单点修改）
2.区间查询

模版题

#include<iostream>
#include<cstdio>using namespace std;const int N = 1e5 + 10;
int C[N],A[N];int n, m;//返回当前数的二进制中最低的一位
int lowbit(int x)
{//将x 转化成2进制, -x是x的补码 = x的反码 + 1return x&-x;
}//加上某个数
void add(int x,int v)
{//加上一个数，后面也要变化(i += lowbit(i))for(int i = x; i <= n; i += lowbit(i))  C[i] += v; 
}//区间和（前缀和）
int query(int x)
{int sum = 0;//求和，往前面求和，  i > 0, i -= lowbit(i) for(int i = x; i > 0; i-= lowbit(i))   sum += C[i];return sum;
}int main()
{scanf("%d %d", &n, &m);for(int i = 1; i <= n; i++) scanf("%d\n", &A[i]);//初始化树状数组(注意这里方法,直接用add函数)for(int i = 1; i <= n; i++) add(i, A[i]);while(m--){int k, a, b;scanf("%d %d %d", &k, &a, &b);if(k == 0)  printf("%d\n", query(b) - query(a - 1));else    add(a, b);}return 0;
}