2024年2月10日力扣题目训练
- 2024年2月10日力扣题目训练
- 551. 学生出勤记录 I
- 557. 反转字符串中的单词 III
- 559. N 叉树的最大深度
- 241. 为运算表达式设计优先级
- 260. 只出现一次的数字 III
- 126. 单词接龙 II
2024年2月10日力扣题目训练
2024年2月10日第十七天编程训练,今天主要是进行一些题训练,包括简单题3道、中等题2道和困难题1道。惰性太强现在才完成,不过之后我会认真完成的。
551. 学生出勤记录 I
链接: 出勤记录
难度: 简单
题目:

运行示例:

思路:
这道题就是一个简单的遍历,只需在遍历时判断是否不符合条件的情况即可。
代码:
class Solution {
public:bool checkRecord(string s) {int re1 = 0;int re2 = 0;for(int i = 0; i < s.size(); i++){if(s[i] == 'A'){re1++;re2 = 0;if(re1 == 2) return false;}else if(s[i] == 'L'){re2++;if(re2 == 3) return false;}else{re2 = 0;}}return true;}
};557. 反转字符串中的单词 III
链接: 反转字符串中的单词
难度: 简单
题目:

运行示例:

思路:
这道题主要是遍历找到空格,根据空格将单词进行反转。
代码:
class Solution {
public:string reverseWords(string s) {int left = 0;string ans;for(int i = 0; i < s.size(); i++){if(s[i] == ' '){string tmp = s.substr(left,i-left);cout<<"asdf:"<<tmp<<endl;reverse(tmp.begin(),tmp.end());ans += tmp;ans += ' ';left = i+1;}}if(left != s.size()){string tmp = s.substr(left,s.size()-left);reverse(tmp.begin(),tmp.end());ans += tmp;}return ans;}
};
559. N 叉树的最大深度
链接: N 叉树的最大深度
难度: 简单
题目:

运行示例:
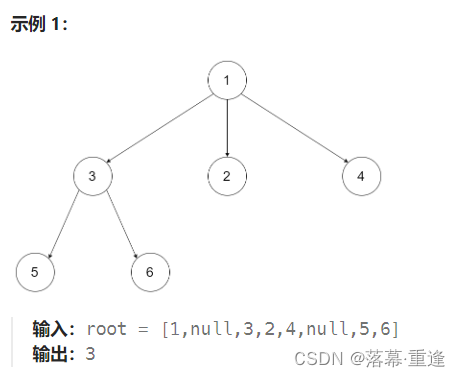
思路:
这道题求N叉树的深度,与543. 二叉树的直径类似,只是从二叉树拓展到N叉树而已。大家也可以先写一下104. 二叉树的最大深度添加链接描述和543. 二叉树的直径进行锻炼之后再写这道题。
代码:
class Solution {
public:int maxDepth(Node* root) {if(root == NULL) return 0;int maxChildDepth = 0;vector<Node*> children = root->children;for(int i = 0; i < children.size(); i++){int childrenDepth = maxDepth(children[i]);maxChildDepth = max(maxChildDepth,childrenDepth);}return maxChildDepth+1;}
};
241. 为运算表达式设计优先级
链接: 优先级
难度: 中等
题目:

运行示例:

思路:
这道题核心就是分治,利用运算符进行分割,递归求解结果。遍历字符串,每次遇到运算符时,将字符串分为运算符左侧和运算符右侧两部分,递归求解这两部分的结果。此外为避免重复计算我们可以利用一个哈希表记录已经计算过的部分。
代码:
class Solution {
public:unordered_map<string,vector<int>> memo;vector<int> findsome(string s){if(memo.find(s) != memo.end()) return memo[s];vector<int> ans;for(int i = 0; i <s.size(); i++){if(!isdigit(s[i])){vector<int> ans1 = findsome(s.substr(0,i));vector<int> ans2 = findsome(s.substr(i+1));if(s[i] == '+'){for(auto& x: ans1)for(auto& y: ans2) ans.push_back(x+y);}else if(s[i] == '-')for(auto& x: ans1)for(auto& y: ans2) ans.push_back(x - y);elsefor(auto& x: ans1)for(auto& y: ans2) ans.push_back(x * y);}}if(ans.empty()) ans.push_back(stoi(s));memo[s] = ans;return ans;}vector<int> diffWaysToCompute(string expression) {return findsome(expression);}
};
260. 只出现一次的数字 III
链接: 只出现一次的数字
难度: 中等
题目:
运行示例:

思路:
这道题考虑位运算,我们知道异或运算有以下性质:
任何数和 0做异或运算,结果仍然是原来的数,即 x⊕0=x;
任何数和其自身做异或运算,结果是 0,即 x⊕x=0;
根据这条性质,我们将数组中的所有数字进行异或运算,得到的结果即为两个只出现一次的数字的异或结果。但由于这两个数字不相等,因此异或结果中至少存在一位为 1。我们可以通过 lowbit 运算找到异或结果中最低位的 1,并将数组中的所有数字按照该位是否为 1分为两组,这样两个只出现一次的数字就被分到了不同的组中。 从而得到结果。
代码:
class Solution {
public:vector<int> singleNumber(vector<int>& nums) {long long sum = 0;for(auto& num:nums) sum ^= num;int lsb = sum &(-sum);int a = 0,b = 0;for (auto& num: nums) {if (num & lsb) {a ^= num;}else {b ^= num;}}return {a,b};}
};
126. 单词接龙 II
链接: 单词接龙
难度: 困难
题目:

运行示例:

思路:
这道题我知道是应该用递归和回溯,但是不知道如何动笔。官方是利用广度优先搜索 + 回溯,建立图。
本题要求的是最短转换序列,看到最短首先想到的就是广度优先搜索。但是本题没有给出显示的图结构,根据单词转换规则:把每个单词都抽象为一个顶点,如果两个单词可以只改变一个字母进行转换,那么说明它们之间有一条双向边。因此我们只需要把满足转换条件的点相连,就形成了一张图。根据示例 1 中的输入,我们可以建出下图:
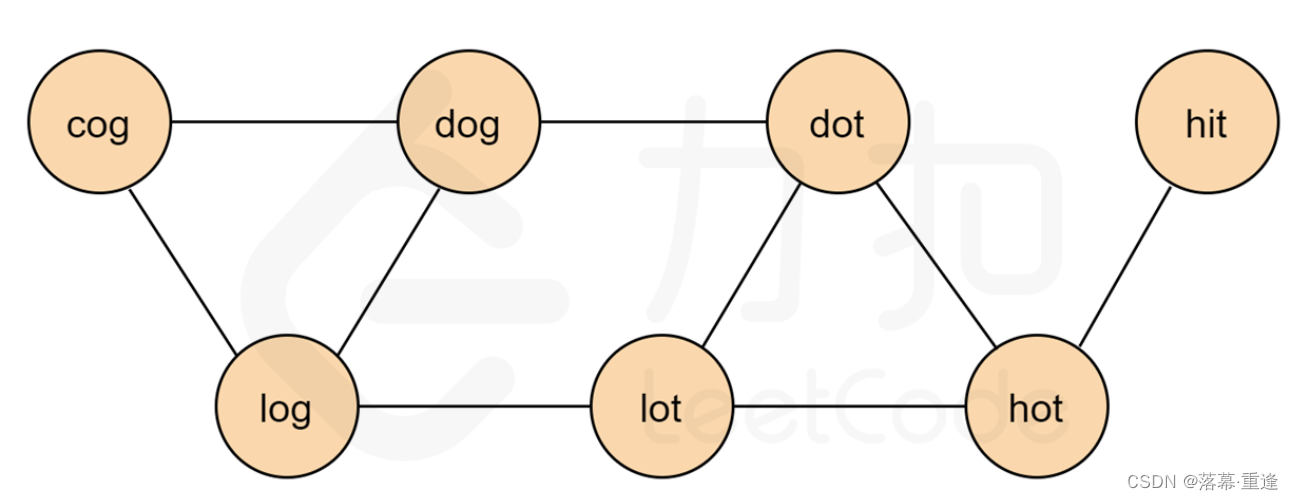
基于该图,我们以 “hit"为图的起点, 以 “cog"为终点进行广度优先搜索,寻找 “hit"到 “cog"的最短路径。下图即为答案中的一条路径。
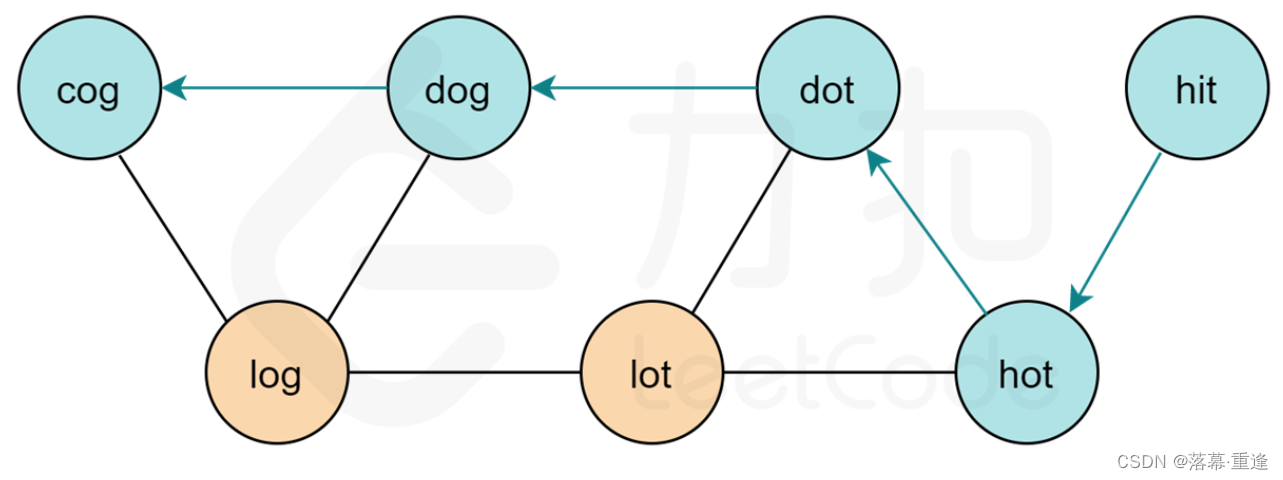
由于要求输出所有的最短路径,因此我们需要记录遍历路径,然后通过回溯得到所有的最短路径。
细节
- 从一个单词出发,修改每一位字符,将它修改成为 ‘a’到 ‘z’中的所有字符,看看修改以后是不是在题目中给出的单词列表中;
- 有一些边的关系,由于不是最短路径上的边,不可以被记录下来。为此,我们为扩展出的单词记录附加的属性:层数。即下面代码中的steps。如果当前的单词扩散出去得到的单词的层数在以前出现过,则不应该记录这样的边的关系。
代码:
class Solution {
public:vector<vector<string>> findLadders(string beginWord, string endWord, vector<string> &wordList) {vector<vector<string>> res;// 因为需要快速判断扩展出的单词是否在 wordList 里,因此需要将 wordList 存入哈希表,这里命名为「字典」unordered_set<string> dict = {wordList.begin(), wordList.end()};// 修改以后看一下,如果根本就不在 dict 里面,跳过if (dict.find(endWord) == dict.end()) {return res;}// 特殊用例处理dict.erase(beginWord);// 第 1 步:广度优先搜索建图// 记录扩展出的单词是在第几次扩展的时候得到的,key:单词,value:在广度优先搜索的第几层unordered_map<string, int> steps = {{beginWord, 0}};// 记录了单词是从哪些单词扩展而来,key:单词,value:单词列表,这些单词可以变换到 key ,它们是一对多关系unordered_map<string, set<string>> from = {{beginWord, {}}};int step = 0;bool found = false;queue<string> q = queue<string>{{beginWord}};int wordLen = beginWord.length();while (!q.empty()) {step++;int size = q.size();for (int i = 0; i < size; i++) {const string currWord = move(q.front());string nextWord = currWord;q.pop();// 将每一位替换成 26 个小写英文字母for (int j = 0; j < wordLen; ++j) {const char origin = nextWord[j];for (char c = 'a'; c <= 'z'; ++c) {nextWord[j] = c;if (steps[nextWord] == step) {from[nextWord].insert(currWord);}if (dict.find(nextWord) == dict.end()) {continue;}// 如果从一个单词扩展出来的单词以前遍历过,距离一定更远,为了避免搜索到已经遍历到,且距离更远的单词,需要将它从 dict 中删除dict.erase(nextWord);// 这一层扩展出的单词进入队列q.push(nextWord);// 记录 nextWord 从 currWord 而来from[nextWord].insert(currWord);// 记录 nextWord 的 stepsteps[nextWord] = step;if (nextWord == endWord) {found = true;}}nextWord[j] = origin;}}if (found) {break;}}// 第 2 步:回溯找到所有解,从 endWord 恢复到 beginWord ,所以每次尝试操作 path 列表的头部if (found) {vector<string> Path = {endWord};backtrack(res, endWord, from, Path);}return res;}void backtrack(vector<vector<string>> &res, const string &Node, unordered_map<string, set<string>> &from,vector<string> &path) {if (from[Node].empty()) {res.push_back({path.rbegin(), path.rend()});return;}for (const string &Parent: from[Node]) {path.push_back(Parent);backtrack(res, Parent, from, path);path.pop_back();}}
};