模板

1.模板概念

模板就是建立通用的模具，大大提高复用性。

模板的特点：

• 模板不可以直接使用，它只是一个框架;
• 模板的通用并不是万能的.

２.泛型编程

泛型编程是一种编程风格，它允许算法和数据结构在不被具体类型限制的情况下编写和执行，从而提高代码的复用性和效率。泛型编程的核心在于使用参数化类型，即类型参数，来定义可以操作多种不同数据类型的通用数据结构和算法。

在泛型编程中，类型参数通常用尖括号包围，如T，它代表一个未知的具体类型，这个类型在编译时被指定，而不是在运行时。泛型类型不是具体的类型，而是类型的模板，类似于对象模板的概念。

• C++另一种编程思想称为 泛型编程 ，主要利用的技术就是模板;
• C++提供两种模板机制:函数模板和类模板 .

1.函数模板

1.1 函数模板语法

函数模板作用：

建立一个通用函数，其函数返回值类型和形参类型可以不具体制定，用一个虚拟的类型来代表。

语法：

template<typename T>
函数声明或定义

解释：

template — 声明创建模板
typename — 表面其后面的符号是一种数据类型，可以用class代替
T — 通用的数据类型，名称可以替换，通常为大写字母

示例：

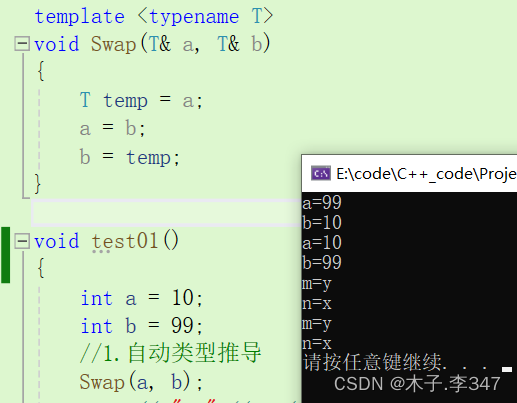
template <typename T>
void Swap(T& a, T& b)
{T temp = a;a = b;b = temp;
}void test01()
{
//整型交换int a = 10;int b = 99;//1.自动类型推导Swap(a, b);cout << "a=" << a << endl;cout << "b=" << b << endl;//2.显示指定类型Swap<int>(a, b);cout << "a=" << a << endl;cout << "b=" << b << endl;//字符型交换char m = 'x';char n = 'y';//1.自动类型推导Swap(m, n);cout << "m=" << m << endl;cout << "n=" << n << endl;//2.显示指定类型Swap<int>(a, b);cout << "m=" << m << endl;cout << "n=" << n << endl;
}

总结：

• 函数模板利用关键字 template
• 使用函数模板有两种方式：自动类型推导、显示指定类型
• 模板的目的是为了提高复用性，将类型参数化.

1.2 函数模板注意事项

注意事项：

• 自动类型推导，必须推导出一致的数据类型T,才可以使用;
• 模板必须要确定出 T 的数据类型，才可以使用;

示例：

template<class T>
void mySwap(T& a, T& b)
{T temp = a;a = b;b = temp;
}// 1、自动类型推导，必须推导出一致的数据类型T,才可以使用
void test01()
{int a = 10;int b = 20;char c = 'c';mySwap(a, b); // 正确，可以推导出一致的T//mySwap(a, c); // 错误，推导不出一致的T类型
}// 2、模板必须要确定出T的数据类型，才可以使用
template<class T>
void func()
{cout << "func 调用" << endl;
}void test02()
{//func(); //错误，模板不能独立使用，必须确定出T的类型func<int>(); //利用显示指定类型的方式，给T一个类型，才可以使用该模板
}

总结：

• 使用模板时必须确定出通用数据类型T，并且能够推导出一致的类型

1.3 普通函数与函数模板的区别

普通函数与函数模板区别：

• 普通函数调用时可以发生自动类型转换（隐式类型转换）；
• 函数模板调用时，如果利用自动类型推导，不会发生隐式类型转换；
• 如果利用显示指定类型的方式，可以发生隐式类型转换（老版VS可以）；

示例：

//普通函数
int add(int a, int b)
{return a + b;
}
//函数模板
template <class T>
T myadd(T& a,T& b)
{return a + b;
}void test01()
{int a = 10;int b = 20;char c = 'A';//ASCII码为65cout << add(a, c) << endl; //正确，将char类型的'A'隐式转换为int类型；输出75//myadd(a, c); // 报错，使用自动类型推导时，不会发生隐式类型转换//myadd<int>(a, c); //不正确，对于VS2022不可以；对于老版VS用显示指定类型，可以发生隐式类型转换
}

1.4 普通函数与函数模板的调用规则

调用规则如下：

1. 如果函数模板和普通函数都可以实现，优先调用普通函数；
2. 可以通过空模板参数列表来强制调用函数模板；
3. 函数模板也可以发生重载；
4. 如果函数模板可以产生更好的匹配,优先调用函数模板；
   示例：

void myPrint(int a, int b)
{cout << "调用的普通函数" << endl;
}template<typename T>
void myPrint(T a, T b)
{cout << "调用的模板" << endl;
}template<typename T>
void myPrint(T a, T b, T c)//重载
{cout << "调用重载的模板" << endl;
}
void test02()
{//1、如果函数模板和普通函数都可以实现，优先调用普通函数// 注意 如果告诉编译器  普通函数是有的，但只是声明没有实现，或者不在当前文件内实现，就会报错找不到int a = 10;int b = 20;myPrint(a, b); //调用普通函数//2、可以通过空模板参数列表来强制调用函数模板---<>myPrint<>(a, b); //调用函数模板//3、函数模板也可以发生重载int c = 30;myPrint(a, b, c); //调用重载的函数模板//4、 如果函数模板可以产生更好的匹配,优先调用函数模板//普通函数无法使用char c1 = 'a';char c2 = 'b';myPrint(c1, c2); //调用函数模板
}

总结：既然提供了函数模板，最好就不要提供普通函数，否则容易出现二义性

1.5 模板的局限性

局限性：

• 模板的通用性并不是万能的

如果模板的数据类型传入的是像Person类这样的自定义数据类型，无法正常运行；
因此C++为了解决这种问题，提供模板的重载，可以为这些特定的类型提供具体化的模板。

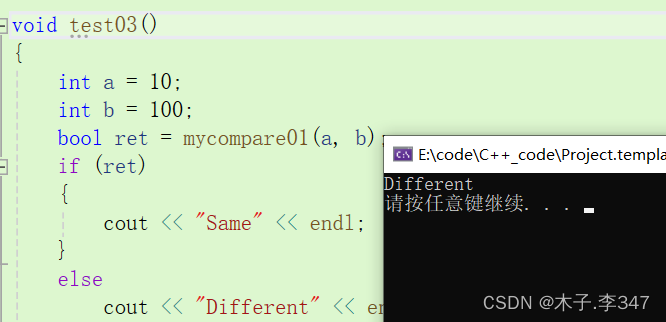
示例1：对比整型

template <class T>
bool mycompare01(T& a, T& b)
{if (a == b){return true;}elsereturn false;
}void test03()
{int a = 10;int b = 100;bool ret = mycompare01(a, b);if (ret){cout << "Same" << endl;}elsecout << "Different" << endl;
}

示例2：对比自定义类型

class Person
{
public:Person(string name, int age){this->m_name = name;this->m_age = age;}string m_name;int m_age;
};//普通函数模板
template<class T>
bool myCompare(T& a, T& b)
{if (a == b){return true;}else{return false;}
}
//具体化，显示具体化的原型和定义是以template<>开头，并通过名称来指出类型
//具体化优先于常规模板
template <> bool myCompare(Person& p1, Person& p2)
{if (p1.m_name==p2.m_name&&p1.m_age==p2.m_age){return true;}elsereturn false;
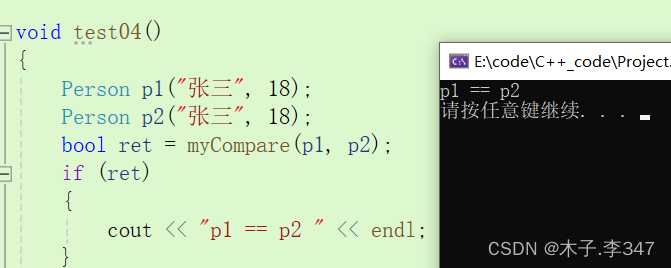
}void test04()
{Person p1("张三", 18);Person p2("张三", 18);bool ret = myCompare(p1, p2);if (ret){cout << "p1 == p2 " << endl;}else{cout << "p1 != p2 " << endl;}
}

**注意：**对于具体化的模板，要先有普通函数模板才可实现，否则报错。如下

报错：“myCompare”不是当前范围内的类或函数模板名称。

总结：

• 利用具体化的模板，可以解决自定义类型的通用化
• 学习模板并不是为了写模板，而是在STL能够运用系统提供的模板

1.6 函数模板案例

案例描述：

• 利用函数模板封装一个排序的函数，可以对不同数据类型数组进行排序
• 排序规则从大到小，排序算法为冒泡排序
• 分别利用char数组和int数组进行测试
  示例

//冒泡排序函数模板
template <class T>
void Sort(T arr[], int len)
{int i = 0;for (i = 0; i < len-1; i++){int j = 0;for (j = 0; j < len - 1 - i; j++){if (arr[j] < arr[j + 1]){T temp = arr[j];arr[j] = arr[j+1];arr[j+1] = temp;}}}
}//打印函数模板
template <class T>
void myPrint(T arr[], int len)
{int i = 0;for (i = 0; i < len; i++){cout << arr[i] << " ";}cout << endl;
}//测试
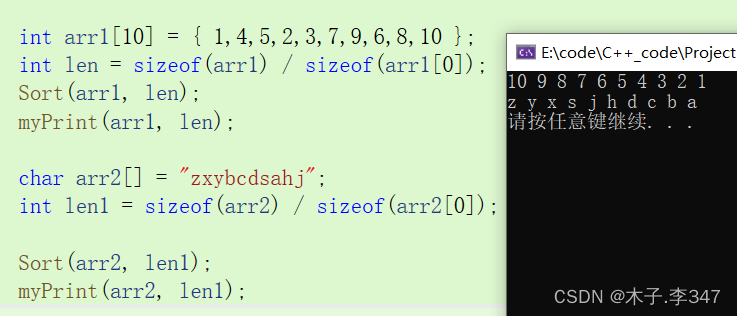
void test01()
{int arr1[10] = { 1,4,5,2,3,7,9,6,8,10 };int len = sizeof(arr1) / sizeof(arr1[0]);Sort(arr1, len);myPrint(arr1, len);char arr2[] = "zxybcdsahj";int len1 = sizeof(arr2) / sizeof(arr2[0]);Sort(arr2, len1);myPrint(arr2, len1);
}