Graph Theory(图论)

Definition 5.1. Intuitively, a graph is just a way of modeling a collection of objects and the connections between them.

直观地说，图只是为对象集合及其之间的连接建模的一种方式。

Definition 5.2. A simple undirected loopless graph G consists of
two things: a collection V of vertices, and another collection E of
edges, which we think of as distinct unordered pairs of distinct elements
in V . We think of the vertices in a graph as the objects we’re studying, and the edges in a graph as a way to describe how those objects are
connected.
To describe an edge connecting a pair of vertices a, b in our graph G, we
use our set language from earlier and write this as {a, b}. We say that
a and b are the endpoints of the edge {a, b} when this happens.

一个简单的无向无环图G由两部分组成:顶点的集合V，和边的集合E，我们认为它们是V中不同元素的不同的无序对。我们把图中的顶点看作是我们正在研究的对象，而图中的边则是描述这些对象之间如何连接的一种方式。
为了描述图G中连接顶点对a, b的一条边，我们使用之前的集合语言，将其写成{a, b}。我们说a和b是边{a, b}的端点。

例如：

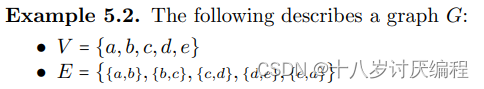
根据以上的定义我们可以画出几种符合要求的图：

Definition 5.3. A simple graph with loops is just like a simple graph
G, except we no longer require the pairs of elements in E to be distinct;
that is, we can have things like {v, v} ∈ E.
A multigraph is a simple graph, except we allow ourselves to repeat
edges in E multiple times; i.e. we could have three distinct edges e1, e2, e3 ∈
E with each equal to the same pair {x, y}.
A directed graph is a simple graph, except we think of our edges as
ordered pairs: i.e. we have things like x → y ∈ E, not {x, y}.
You can mix-and-match these definitions: you can have a directed graph
with loops, or a multigraph with loops but not directions, or pretty much
anything else you’d want!

带有循环的简单图就像简单图G一样，只是我们不再要求E中的元素对是不同的;也就是说，我们可以有{v, v}∈E。

多重图是一个简单的图，除了我们允许我们自己多次重复E中的边;也就是说，我们有三条不同的边e1 e2 e3∈E和每一个都等于相同的一对{x, y}。

一个有向图是一个简单的图，除了我们认为我们的边是有序对:例如，我们有x→y∈E，而不是{x, y}。

您可以混合使用这些定义:您可以使用带有循环的有向图，或者使用带有循环但没有方向的多重图，或者几乎任何您想要的东西!

我们可以看几个示例图片：

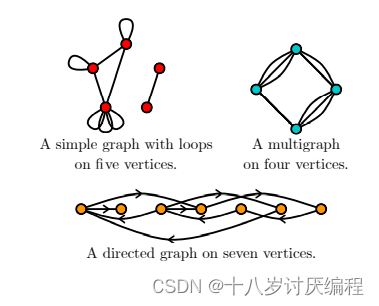
接下来列举出一些较为特殊的图：

Definition 5.4. The complete graph on n vertices Kn is defined for
any positive integer n as follows: take n vertices. Now, take every possible pair of distinct vertices, and connect them with an edge! We draw
several examples at right.
In this sense, a complete graph is a graph in which we have as manyedges as is possible for a graph on n vertices.

对于任意正整数n, n个顶点上的完整图Kn定义如下:取n个顶点。现在，取每一对可能的不同顶点，并将它们与一条边连接起来!

从这个意义上说，一个完整图是这样一个图，它有尽可能多的边对于一个有n个顶点的图来说。
例如：

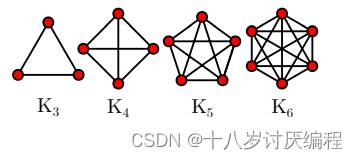
Definition 5.6. The cycle graph on n vertices Cn is defined for any
integer n ≥ 3 as follows: take n vertices, and label them 1, 2, . . . n. Now,draw edges {1, 2},{2, 3}, . . . until you get to the last edge {n− 1, n}; thenconnect this up into a closed cycle by drawing {n, 1} as an edge as well.

对于任意n≥3的整数，定义n个顶点Cn上的循环图如下:取n个顶点，标为1,2，…n.现在，绘制边{1,2}，{2,3}，…直到最后一条边{n−1,n};然后将其连接成一个闭合循环，将{n, 1}也画成一条边。
例如：

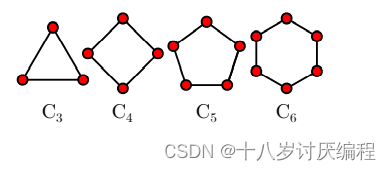
Graphs: Useful Concepts(图：有用的概念)

Definition 5.7. Take a graph G. We say that two vertices a, b in G are
adjacent if the edge {a, b} is in G. We say that a and b are neighbors
if they are adjacent.

以一个图G为例，如果边{a, b}在G中，我们说G中的两个顶点a, b是相邻的，我们可以说a，b两个顶点是neighbors

Definition 5.8. Take a graph G, and a vertex v in G. We say that the
degree of v, written deg(v), is the number of edges that contain v as an
endpoint.

以一个图G和G中的一个顶点v为例，我们说v的度，写成deg(v)，是包含v作为端点的边的数量。

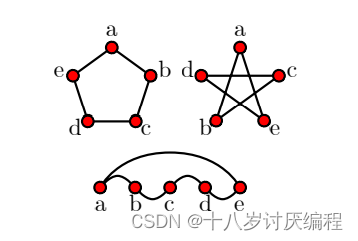
例如：对于如下的图：

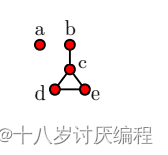
顶点a的度为0，顶点b的度为1，顶点d和e的度为2，顶点c的度为3。

Claim 5.1. (The “degree-sum formula,” or “handshaking theorem.”)
Take any graph G. Then, the sum of the degrees of all of the vertices in
G is always two times the number of edges in G.

取任意图G，所有顶点的度数之和总是的边数的两倍。

Claim 5.2. You cannot have a graph on seven vertices in which the
degree of every vertex is 3.

你不可能有一个有七个顶点的图每个顶点的度数都是3。

Walks and connectedness(走法和连通性)

Definition 5.9. In a graph G, we define a walk of length n as any
sequence of n edges from G of the form
{v0, v1}, {v1, v2}, {v2, v3}, . . . , {vn−1, vn}.
We say that this walk starts at v0 and ends at vn.
We say that a walk is a circuit or closed walk if it starts where it ends;
i.e. if v0 = vn.
We say that a walk is a path if it does not repeat any vertices, with the
following exception: if the first and last vertex of path are the same and
all of the others are distinct, we allow this to be a path as well. In this
last case, we call our walk a cycle.
We often describe a walk by just listing its vertices in order: i.e.
v0 → v1 → v2 → . . . → vn−1 → vn
is a valid way to describe a walk.

在图G中，我们定义了一个长度为n的步长，即从图G出发的任意n条边的序列

对于：
{v0, v1}, {v1, v2}, {v2, v3}, . . . , {vn−1, vn}.

这段路程从v0开始，到vn结束。
如果步行从终点开始，我们就称其为环行或封闭的步行;即如果v0 = vn。
我们说一次行走是一条路径，如果它没有重复任何顶点，除了以下的例外:如果路径的第一个和最后一个顶点是相同的，并且所有其他的顶点是不同的，我们允许它也是一条路径。在最后一种情况下，我们称之为步行周期。

我们经常通过按顺序列出它的顶点来描述一次行走。
v0→v1→v2→…→vn−1→vn是描述步行的有效方法。

注意，行走可以重复边和顶点!

Definition 5.10. Given a graph G, we say that G is connected if for
every pair of vertices a, b in G, there is a path from a to b in G.

给定一个图G，如果对于G中的每一对顶点a, b，在G中有一条从a到b的路径,我们说G是连通的，