二叉搜索树
二叉搜索树: 又为搜索二叉树,一般具有以下的性质
- 若它的左子树不为空,则左子树上所有的节点的值都小于父亲节点
- 若它的右子树不为空,则右子树上所有的节点的值都大于父亲节点
- 它的左右子树也都为二叉搜索树
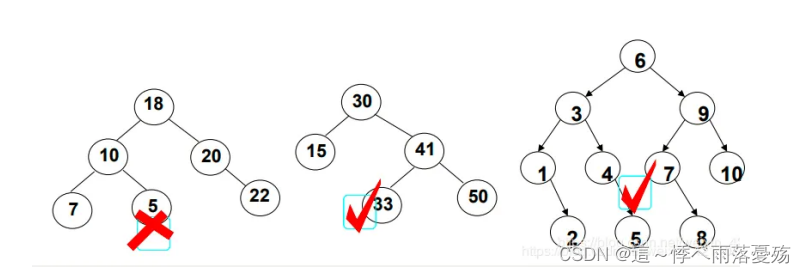
二叉搜索树操作:
以下面图示例子
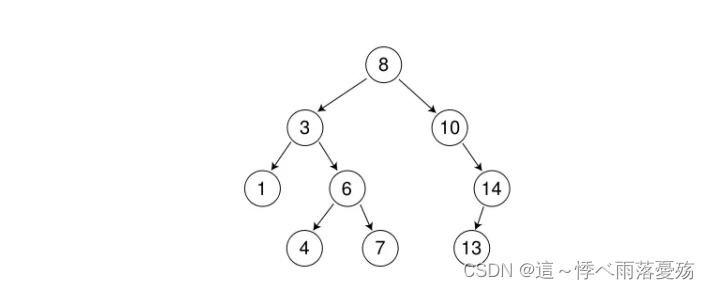
int a[] = {8, 3, 1, 10, 6, 4, 7, 14, 13};
1、二叉搜索树的查找
- 从根开始比较,查找,比根大就往右子树走,比根小就往左子树走
- 最多查找树的高度,如果走到空,就说明没有这个值,查找失败
bool Find(const K& key){Node* cur = _root;if(cur->_key> key){cur = cur->_left;}else if(cur->_key < key){cur = cur->_right;}else {return true;}return false;}
2、二叉搜索树的插入
插入的具体过程如下:
- 树为空,则直接新增节点,赋值给root指针
- 树不为空,按二叉搜索树性质查找新增位置,插入新增节点
- 如果插入的值与它本身的值相等,就失败,二叉搜索树中不能有相同的值

bool Insert(const K& key){//判断是不是空if(_root == nullptr){_root = new Node(key);return true;}//不是空,就插入Node* cur = _root;Node* parent = nullptr;while(cur){if(cur->_key > key){parent = cur;cur = cur->_left;}else if(cur->_key < key){parent = cur;cur = cur->_right;}else{return false;}}//到这里说明是空cur = new Node(key);//链接if(parent->_key > key)parent->_left = cur;else parent->_right = cur;return true;}
3、二叉搜索树的删除
首先查找元素是否存在二叉搜索树中,如果不存在,则返回,否则要删除的节点要分以下四种情况:
- 要删除的节点无孩子节点
- 要删除的节点只有左孩子
- 要删除的节点只有右孩子
- 要删除的节点有左右孩子
首先这里可以说是三种情况,因为如果没有孩子节点,那么就会进入到只有左孩子或者只有右孩子的节点的情况。
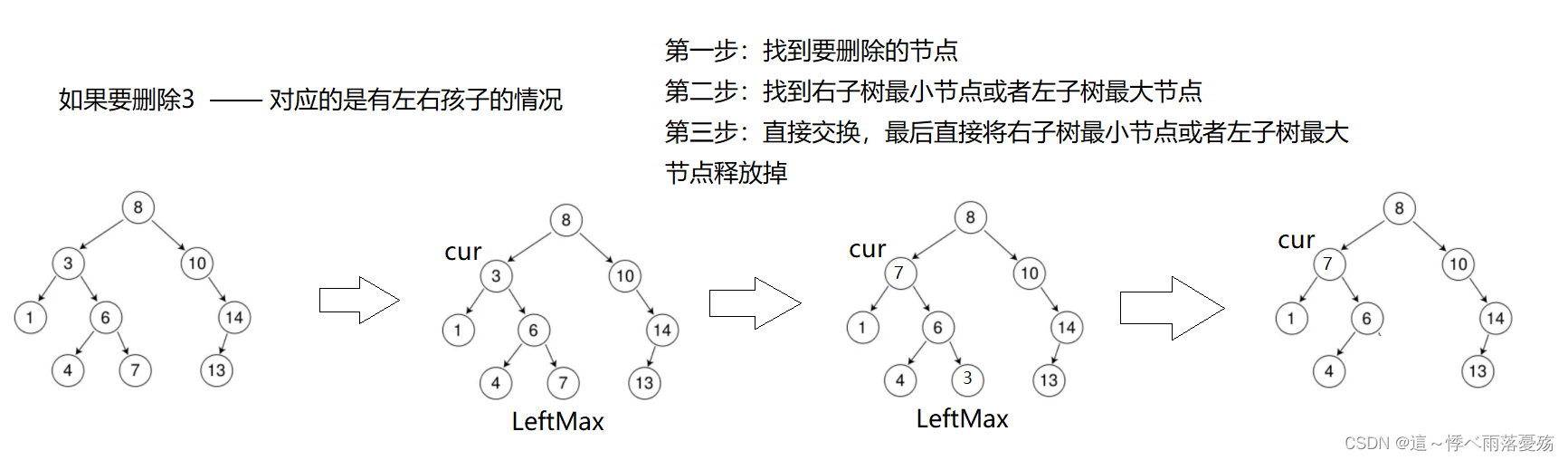
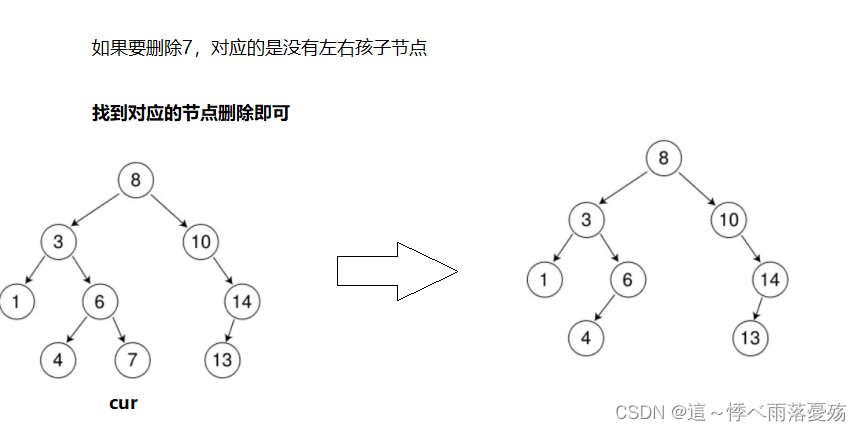
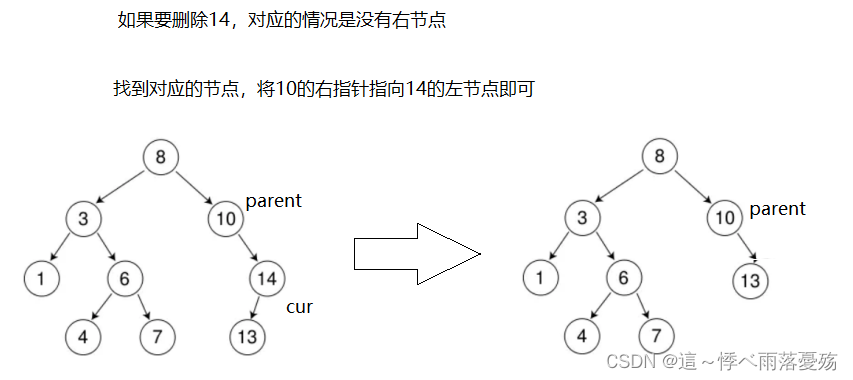
bool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while(cur){if(cur->_key > key){parent = cur;cur = cur->_left;}else if(cur->_key < key){parent = cur;cur = cur->_right;}else{//cur的左为空if(cur->_left == nullptr){if(cur == _root)_root = cur->_right;else{if(cur == parent->_left){parent->_left = cur->_right;}else if(cur == parent->_right){parent->_right = cur->_right;}}delete cur;return true; }else if(cur->_right == nullptr)// cur->_right为空{if(cur == _root)_root = cur->_right;else {if(cur == parent->_left)parent->_left = cur->_left;else if(cur == parent->_right)parent->_right = cur->_left;}delete cur;return true;}else{//替换法 右数最小节点或者左树最大节点,然后赋值,删除最小/最大节点//如果都不为空Node* rightMinParent = cur; //这里必须赋值为cur,因为如果是头删这里就会有问题Node* rightMin = cur->_right;//找右数中最小的值while(rightMin->_left){rightMinParent = rightMin;rightMin = rightMin->_left;}cur->_key = rightMin->_key;//此时rightMin的左子树为空,右子树可能有值if(rightMin == rightMinParent->_left)rightMinParent->_left = rightMin->_right;else rightMinParent->_right = rightMin->_right;delete rightMin;return true;}}}return false;}
二叉搜索树的性能分析:
二叉搜索树的插入和删除操作都需要查找,所以查找是二查搜索树中的性能关键。
如果有n个节点的二叉搜索树,若每个元素查找的概率相等,则二叉搜索树的平均查找长度的关键就在于树的深度。
如果树是一颗二叉平衡搜索二叉树,那么查找的效率就是O(logN)
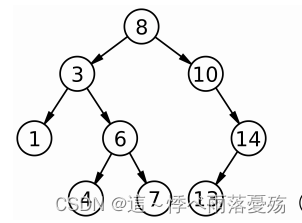
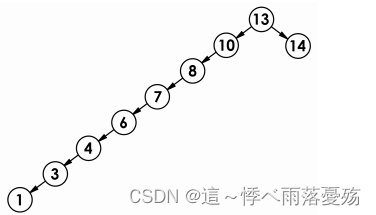
当然也有特殊的场景,如下图所示,它的查找效率就会变得非常慢,平均比较次数就达到了O(N^2)