二叉树高频题目(不含树形DP)

二叉树高频题

二叉树的层序遍历

. - 力扣（LeetCode）

按点弹出

class Solution {
public:vector<vector<int>> levelOrder(TreeNode* root) {vector<vector<int>>ans;if(root!=nullptr){queue<TreeNode*>q;unordered_map<TreeNode*,int>levels;q.push(root);levels[root]=0;while(!q.empty()){auto cur=q.front();q.pop();int level=levels[cur];if(ans.size()==level){ans.push_back(vector<int>());}ans[level].push_back(cur->val);if(cur->left!=nullptr){q.push(cur->left);levels[cur->left]=level+1;}if(cur->right!=nullptr){q.push(cur->right);levels[cur->right]=level+1;}}}return ans;}
};

按层弹出

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:vector<vector<int>> levelOrder(TreeNode* root) {vector<vector<int>>ans;if(root!=nullptr){queue<TreeNode*>q;q.push(root);while(!q.empty()){int size=q.size();vector<int>tmp;for(int i=0;i<size;i++){auto cur=q.front();q.pop();tmp.push_back(cur->val);if(cur->left!=nullptr){q.push(cur->left);}if(cur->right!=nullptr){q.push(cur->right);}}ans.push_back(tmp);}  }return ans;}
};

二叉树的锯齿形遍历

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/const int N=2222;class Solution {TreeNode* q[N];
public:vector<vector<int>> zigzagLevelOrder(TreeNode* root) {vector<vector<int>>ans;if(root!=nullptr){int l=0,r=0;q[r++]=root;bool reverse=false;  //false 左->右while(l<r){int levelSize=r-l;vector<int>curLevel;for(int i=reverse?r-1:l,j=reverse?-1:1,k=0;k<levelSize;k++,i+=j){auto cur=q[i];curLevel.push_back(cur->val);}for(int i=0;i<levelSize;i++){auto cur=q[l++];if(cur->left!=nullptr)q[r++]=cur->left;if(cur->right!=nullptr)q[r++]=cur->right;}ans.push_back(curLevel);reverse=!reverse;}}return ans;}
};

二叉树的最大特殊宽度

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
const int N=3333;
typedef unsigned long long LL;
class Solution {TreeNode* nq[N];LL iq[N];
public:int widthOfBinaryTree(TreeNode* root) {LL ans=1;int l=0,r=0;nq[r]=root;iq[r++]=1;while(l<r){int levelSize=r-l;ans=max(ans,iq[r-1]-iq[l]+1);for(int i=0;i<levelSize;i++){auto cur=nq[l];LL id=iq[l++];if(cur->left!=nullptr){nq[r]=cur->left;iq[r++]=id*2;}if(cur->right!=nullptr){nq[r]=cur->right;iq[r++]=id*2+1;}}}return (int)ans;}
};

二叉树的最大深度

二叉树的最小深度

二叉树的序列化和反序列化

先序

class Codec {
public:// Encodes a tree to a single string.string serialize(TreeNode* root) {ostringstream out;serialize(root,out);return out.str();}void serialize(TreeNode* node, ostringstream& out) {if(!node)out<<"#,";else{out<<node->val<<',';serialize(node->left,out);serialize(node->right,out);}}TreeNode* deserialize(string data) {istringstream in(data);return deserialize(in);}TreeNode* deserialize(istringstream& in) {string val;if(!getline(in,val,','))return nullptr;if(val=="#")return nullptr;TreeNode* node=new TreeNode(stoi(val));node->left=deserialize(in);node->right=deserialize(in);return node;}};

中序没有序列化

层序

class Codec {
public:// 序列化std::string serialize(TreeNode* root) {std::string data;if (root != nullptr) {std::queue<TreeNode*> q;q.push(root);while (!q.empty()) {TreeNode* node = q.front();q.pop();if (node != nullptr) {data += std::to_string(node->val) + ",";q.push(node->left);q.push(node->right);} else {data += "#,";}}}return data;}// 反序列化TreeNode* deserialize(const std::string& data) {if (data.empty()) return nullptr;std::stringstream ss(data);std::string item;getline(ss, item, ',');TreeNode* root = new TreeNode(std::stoi(item));std::queue<TreeNode*> q;q.push(root);while (!q.empty()) {TreeNode* node = q.front();q.pop();if (!getline(ss, item, ',')) break;if (item != "#") {node->left = new TreeNode(std::stoi(item));q.push(node->left);}if (!getline(ss, item, ',')) break;if (item != "#") {node->right = new TreeNode(std::stoi(item));q.push(node->right);}}return root;}
};

已知先序和中序建树

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {if(preorder.empty()||inorder.empty()||preorder.size()!=inorder.size()){return nullptr;}unordered_map<int,int> mp;for(int i=0;i<inorder.size();i++){mp[inorder[i]]=i;}return f(preorder,0,preorder.size()-1,inorder,0,inorder.size()-1,mp);}TreeNode* f(vector<int>&pre,int l1,int r1,vector<int>&in,int l2,int r2,unordered_map<int,int>mp){if(l1>r1)return nullptr;TreeNode* head=new TreeNode(pre[l1]);if(l1==r1)return head;int k=mp[pre[l1]];head->left=f(pre,l1+1,l1+k-l2,in,l2,k-1,mp);head->right=f(pre,l1+k-l2+1,r1,in,k+1,r2,mp);return head;}
};

验证完全二叉树

完全二叉树：在一棵二叉树中，除了最后一层外，每一层都被完全填满，并且所有节点都尽可能地集中在左侧。

完全二叉树具有以下特性：

层级填充：除了最后一层，其他每一层的节点数都达到最大个数。
左侧偏重：最后一层的节点集中在左侧，这层的节点可能不是满的，但如果有空缺，那么空缺部分一定在右侧。
序号特性：如果将所有节点从上至下、从左至右编号，第i个节点的左子节点编号为2*i，右子节点编号为2*i+1（这里假设根节点编号为1）。这是因为完全二叉树可以用数组来顺序存储，且这种存储方式不会浪费空间。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/const int N=333;
class Solution {TreeNode* q[N];
public:bool isCompleteTree(TreeNode* root) {if(root==nullptr)return true;int l=0,r=0;q[r++]=root;//是否遇到孩子不全的节点bool leaf=false;while(l<r){auto cur=q[l++];if((cur->left==nullptr&&cur->right!=nullptr)||(leaf&&(cur->left!=nullptr||cur->right!=nullptr))){return false;}if(cur->left!=nullptr)q[r++]=cur->left;if(cur->right!=nullptr)q[r++]=cur->right;if(cur->left==nullptr||cur->right==nullptr)leaf=true;}return true;}
};

求完全二叉树节点个数

. - 力扣（LeetCode）

满二叉树公式

k=h第k层的结点数是：2^(k-1)； 总结点数是：2^k-1 (2的k次方减一)，总节点数一定是奇数。

递归思路

如果能扎到最深层则是满二叉树

如果不能扎到最深层

串一遍

时间复杂度

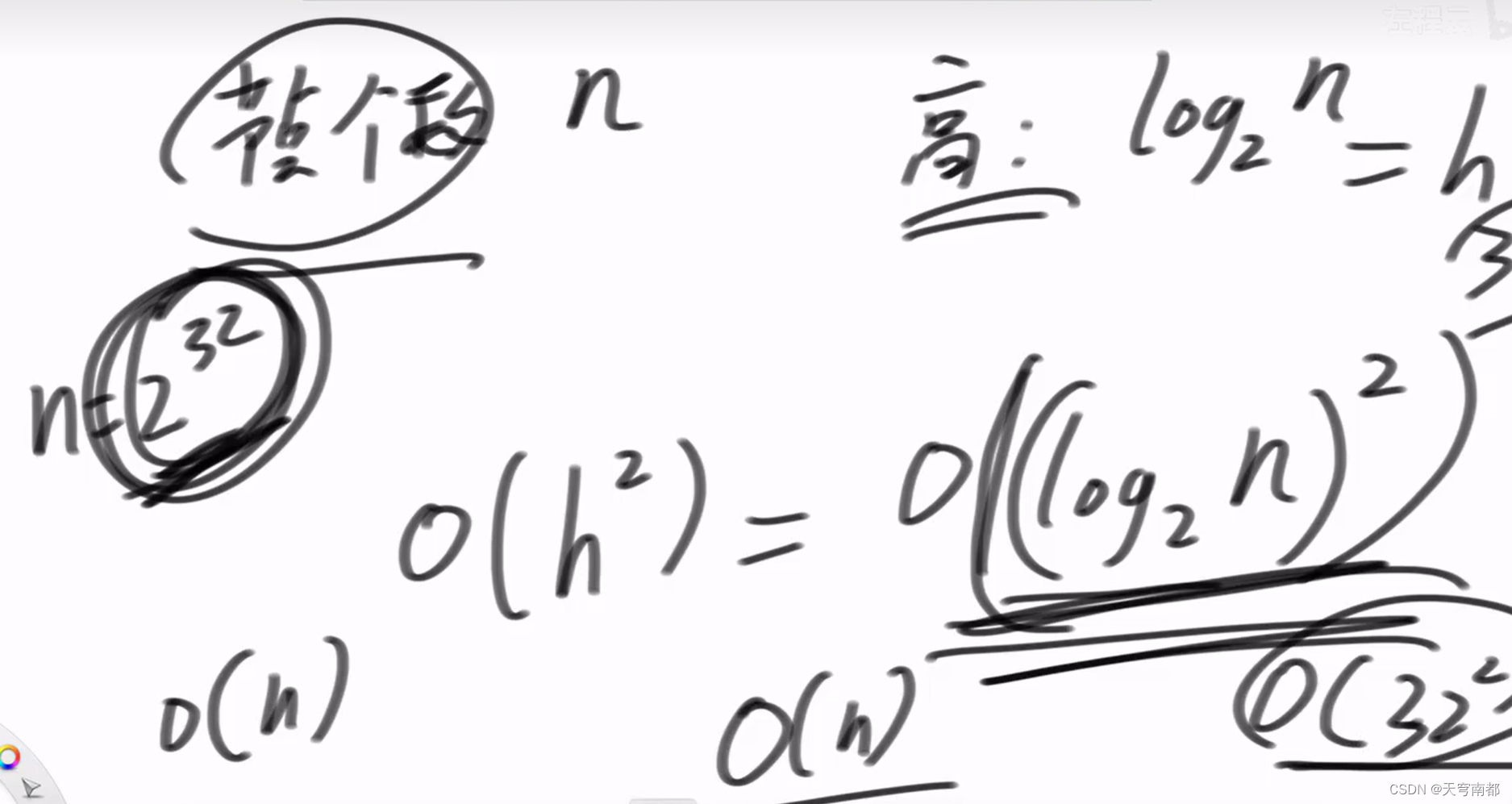
/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int countNodes(TreeNode* root) {if(root==nullptr)return 0;return f(root,1,mostLeft(root,1));}//cur当前节点//level当前层//h最深层数int f(TreeNode* cur,int level,int h){if(level==h)return 1;//cur右树的最左节点能扎到最深层if(mostLeft(cur->right,level+1)==h){return (1<<(h-level))+f(cur->right,level+1,h);}else{return (1<<(h-level-1))+f(cur->left,level+1,h);}}int mostLeft(TreeNode* cur,int level){while(cur!=nullptr){level++;cur=cur->left;}return level-1;}
};

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/264217.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！