01背包问题

Leetcode 1049. 最后一块石头的重量 II 

题目链接：1049 最后一块石头的重量 II

题干：有一堆石头，用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。

每一回合，从中选出任意两块石头，然后将它们一起粉碎。假设石头的重量分别为 x 和 y，且 x <= y。那么粉碎的可能结果如下：

• 如果 x == y，那么两块石头都会被完全粉碎；
• 如果 x != y，那么重量为 x 的石头将会完全粉碎，而重量为 y 的石头新重量为 y-x。

最后，最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下，就返回 0。

思考：动态规划。难点在于：想到尽量让石头分成重量相同的两堆，相撞之后剩下的石头最小。从而可以看出是01背包问题的类似题。

---

• 确定dp数组以及下标的含义

dp[j]表示容量（或可承受重量）为j的背包，最多能装下的价值（石头总重量）。

• 确定递推公式

01背包的递推公式为：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

本题为：dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);

• dp数组如何初始化

由于想将石头分成两堆，因此数组的大小只要能装下总重量的一半即可。

此外由于重量不可能为负数，dp[i]都初始为0即可。

• 确定遍历顺序

由于使用一维dp数组，物品遍历的for循环放在外层，遍历背包的for循环放在内层，且内层for循环倒序遍历。

• 举例推导dp数组

举例，输入：[2,4,1,1]，dp数组状态图如下：

最后dp[sum / 2]里是容量为sum / 2的背包所能背的最大重量。 那么分成两堆石头，一堆石头的总重量是dp[sum / 2]，另一堆就是sum - dp[sum / 2]。

sum / 2 因为是向下取整，所以sum - dp[sum / 2] 一定是大于等于dp[sum / 2]的。那么相撞之后剩下的最小石头重量就是 (sum - dp[sum / 2]) - dp[sum / 2]。

代码：

class Solution {
public:int lastStoneWeightII(vector<int>& stones) {int sum = 0;for (int n : stones)     //统计石头总重量sum += n;vector<int> dp(sum / 2 + 1, 0);     //dp[i]表示容量为i的背包装下的石头总重量for (int i = 0; i < stones.size(); i++)         //遍历石头for (int j = sum / 2; j >= stones[i]; j--)  //遍历背包容量,只考虑放得下的情况dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);      //递推公式return sum - dp[sum / 2] - dp[sum / 2];}
};

Leetcode 494. 目标和

题目链接：494 目标和

题干：给你一个非负整数数组 nums 和一个整数 target 。

向数组中的每个整数前添加 '+' 或 '-' ，然后串联起所有整数，可以构造一个 表达式 ：

• 例如，nums = [2, 1] ，可以在 2 之前添加 '+' ，在 1 之前添加 '-' ，然后串联起来得到表达式 "+2-1" 。

返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。

难点：此题的难点在于如何使表达式结果为target。

若从往数字前面添加正负号的角度去思考，此题较难处理。

若将问题看成划分数组成两堆，一堆加正号（记作左堆left），另一堆加负号（记作右堆right），两堆相加（left - right）结果为target，则解题目标从计算添加正负号形成不同表达式的数目转换为计算数组累加结果为left的组合个数。至于left大小：
首先left - right = target；

其次left + right = sum(数组内所有数字相加之和)，从而left = (target + sum) / 2.

当然此题需要剪枝，若sum < target则所有数字相加都达不到目标值即不存在想要的表达式。

其次 由于left是累加之和为整数，则若target + sum 为奇数则也不存在想要的表达式。

思考一：回溯法。此题在理清难点后，和39 组合总和类似。终止条件为累计值为目标值left。由于每种组合数组中的数字只能取一次，因此参数要加上startIndex。

代码：

class Solution {
public:int result = 0;void backtracking(const vector<int>& nums, const int target, int sum, int startIndex) {if (sum == target) {        //找到匹配目标值result++; return;}       for (int i = startIndex; i < nums.size(); i++)      //从startIndex开始遍历，不重复取数if (sum + nums[i] <= target)backtracking(nums, target, sum + nums[i], i + 1);}int findTargetSumWays(vector<int>& nums, int target) {int sum = 0;for (int n : nums)sum += n;if (sum < target || - sum > target)   return 0;       //总和小于目标值绝对值则不存在表达式if ((sum + target) % 2 == 1)    return 0;       //作为正数的累计值必须为整数int left = (sum + target) / 2;      //所需正数的累加之和backtracking(nums, left, 0, 0);return result;}
};

思考二：动态规划。由于每种组合数组中的数字只能取一次，因此考虑01背包。

• 确定dp数组以及下标的含义

dp[j] 表示：从数组中任选数字，累加和为i的选取方式的数目

• 确定递推公式

从dp[ i ]的定义，可以看出有多个方向可以推出dp[ i ]的部分。

当处理的数字为nums[ j ]时，dp[ i ] 的部分可以从累加为 i - nums[ j ]的情况加上nums[ j ]得到。

因此只要搞到nums[ j ]，凑成dp[ j ]就有dp[ j - nums[i] ] 种方法。

例如：dp[j]，j 为5，

• 已经有一个1（nums[i]） 的话，有 dp[4]种方法 凑成 容量为5的背包。
• 已经有一个2（nums[i]） 的话，有 dp[3]种方法 凑成 容量为5的背包。
• 已经有一个3（nums[i]） 的话，有 dp[2]中方法 凑成 容量为5的背包
• 已经有一个4（nums[i]） 的话，有 dp[1]中方法 凑成 容量为5的背包
• 已经有一个5 （nums[i]）的话，有 dp[0]中方法 凑成 容量为5的背包

那么凑整dp[5]有多少方法呢，也就是把 所有的 dp[j - nums[i]] 累加起来。

从而递推公式为dp[j] += dp[j - nums[i]]。

• dp数组如何初始化

从递推公式可以看出，在初始化的时候dp[0] 一定要初始化为1，因为dp[0]是在公式中一切递推结果的起源，如果dp[0]是0的话，递推结果将都是0。

如果数组[0] ，target = 0，那么 bagSize = (target + sum) / 2 = 0。 dp[0]也应该是1， 也就是说给数组里的元素 0 前面无论放加法还是减法，都是 1 种方法。

所以本题我们应该初始化 dp[0] 为 1。

dp[j]其他下标对应的数值也应该初始化为0，从递推公式也可以看出，dp[j]要保证是0的初始值，才能正确的由dp[j - nums[i]]推导出来。

• 确定遍历顺序

对于01背包问题一维dp的遍历，nums放在外循环，target在内循环，且内循环倒序。

• 举例推导dp数组

举例：nums: [1, 1, 1, 1, 1], target: 3。此时bagSize = (target + sum) / 2 = (3 + 5) / 2 = 4。

dp数组状态变化如下：

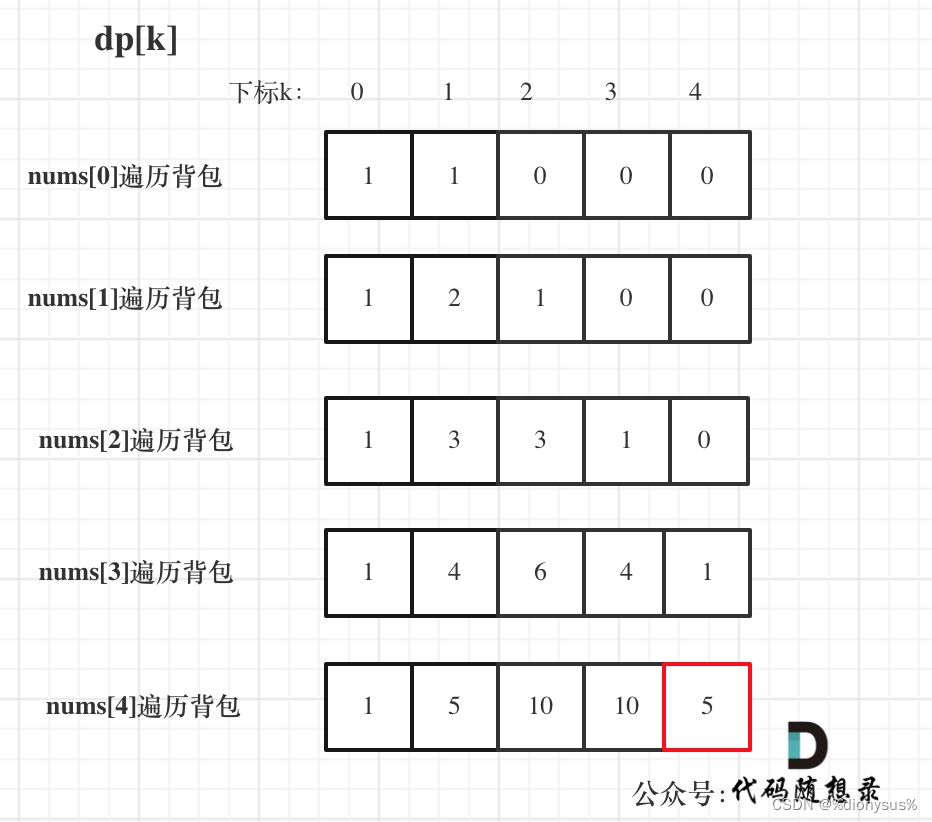
代码：

class Solution {
public:int findTargetSumWays(vector<int>& nums, int target) {int sum = 0;for (int n : nums)sum += n;if (sum < target || - sum > target)   return 0;       //总和小于目标值绝对值则不存在表达式if ((sum + target) % 2 == 1)    return 0;       //作为正数的累计值必须为整数int left = (sum + target) / 2;      //所需正数的累加之和vector<int> dp(left + 1, 0);        //dp[i]表示从数组中任选数字，累加和为i的选取方式的数目dp[0] = 1;      //初始化for (int i = 0; i < nums.size(); i++)           //遍历数字for (int j = left; j >= nums[i]; j--)        //遍历累加和的形成方式数目dp[j] += dp[j - nums[i]];       //递推公式 累加各种累加途径的数目return dp[left];}
};

Leetcode 474.一和零

题目链接：474 一和零

题干：给你一个二进制字符串数组 strs 和两个整数 m 和 n 。

请你找出并返回 strs 的最大子集的长度，该子集中 最多 有 m 个 0 和 n 个 1 。

如果 x 的所有元素也是 y 的元素，集合 x 是集合 y 的 子集 。

思考：动态规划。本题中strs 数组里的元素就是物品，每个物品都是一个！而m 和 n相当于是一个背包，两个维度的背包。因此本题仍为01背包问题的类似题。

---

• 确定dp数组（dp table）以及下标的含义

dp[i][j]：规定集合中0的个数为i，1的个数为j下，集合中最大元素个数

• 确定递推公式

dp[i][j] 可以由前一个strs里的字符串推导出来，strs里的字符串有zeroNum个0，oneNum个1。

dp[i][j] 就可以是 dp[i - zeroNum][j - oneNum] + 1。遍历的过程中取dp[i][j]的最大值。

因此递推公式：dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);

字符串的zeroNum和oneNum相当于01背包问题中的物品重量（weight[i]），字符串本身的个数相当于物品的价值（value[i]）。

• dp数组如何初始化

因为物品价值不会是负数，所以初始为0，保证递推的时候dp[i][j]不会被初始值覆盖。

• 确定遍历顺序

01背包是外层for循环遍历物品，内层for循环遍历背包容量且从后向前遍历！

那么本题也是，物品就是strs里的字符串，背包容量就是题目描述中的m和n。遍历背包容量的两层for循环先后循序没什么讲究，都只是物品重量的一个维度。

• 举例推导dp数组

举例：["10","0001","111001","1","0"]，m = 3，n = 3。最后dp数组的状态如下所示：

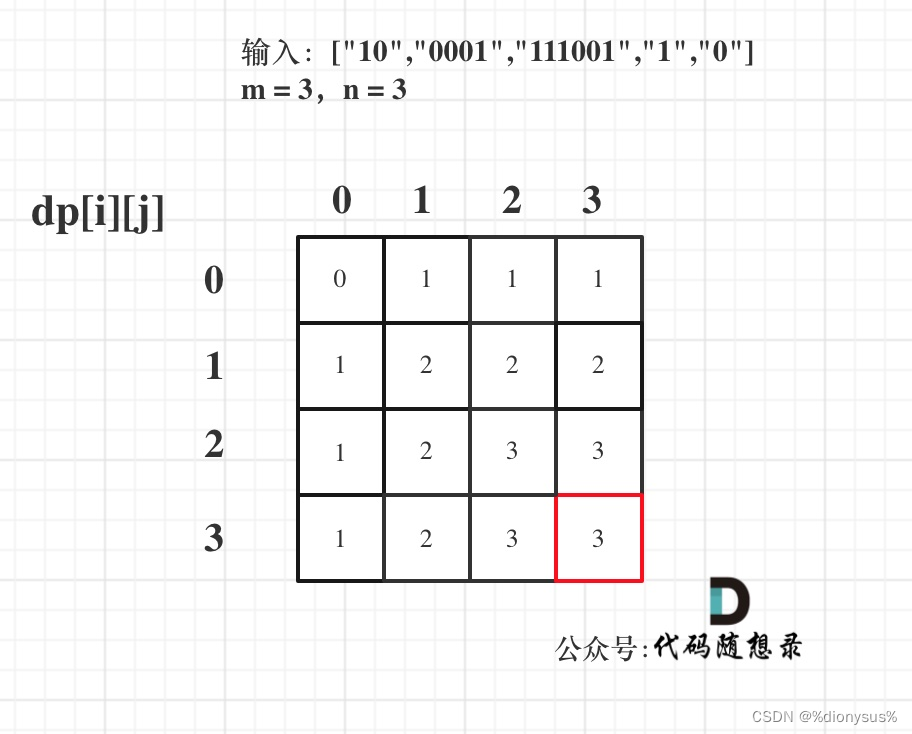
代码：

class Solution {
public:int findMaxForm(vector<string>& strs, int m, int n) {  vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));     //dp[i][j]表示规定集合中0的个数为i，1的个数为j下，集合中最大元素个数for (string str : strs) {      //遍历字符串int zeroNum = 0;for (int i = 0; i < str.size(); i++)        //统计字符串中0的个数if (str[i] == '0')zeroNum++;int oneNum = str.size() - zeroNum;      //记录字符串中1的个数for (int i = m; i >= zeroNum; i--)         //遍历规定集合中0的个数for (int j = n; j >= oneNum; j--)     //遍历规定集合中1的个数dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);      //递推公式}                return dp[m][n];}
};

自我总结：

清晰01背包问题的判断理由：物品不可重复取。确定背包容量，物体重量以及物品价值，考虑dp数组元素的来源来确定递推公式，最后确定数组初始化情况以及dp数组遍历顺序，便可举例验证。