LCR 102. 目标和 - 力扣（LeetCode）

分析题意，画出决策树，其他的思路都跟前面讲过的类似： 

 

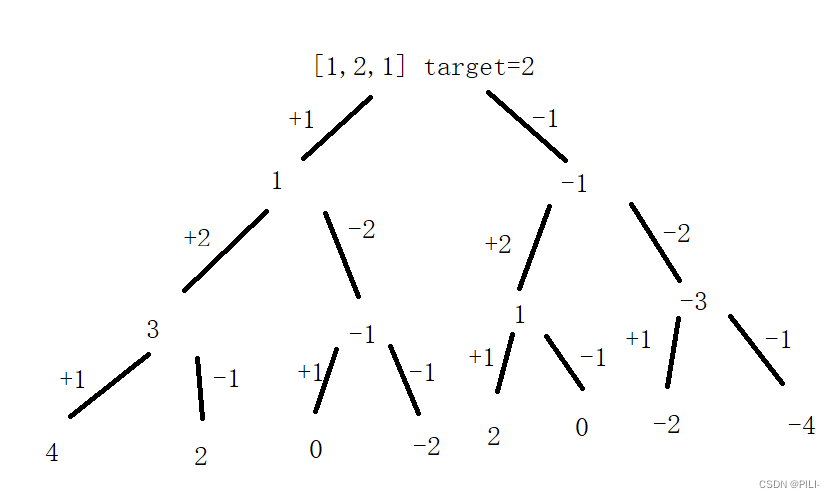
全局变量引入实现： 

全局变量的引入，需要手动处理回溯；

class Solution {int ret;    // 最终结果int sum;    public int findTargetSumWays(int[] nums, int target) {dfs(nums,target,0);return ret;}// pos 表示当前针对 nums[pos] 进行操作public void dfs(int[] nums,int target,int pos){// 递归出口if(pos == nums.length){if(sum == target){ret++;}return;}// 加sum = sum + nums[pos];dfs(nums,target,pos+1);sum = sum - nums[pos];        // 回溯// 减sum = sum - nums[pos];dfs(nums,target,pos+1);sum = sum + nums[pos];        // 回溯}
}

参数引入实现：

参数引入，回溯是默认实现的，sum值在每一层都是不变化的；

class Solution {int ret;    // 最终结果public int findTargetSumWays(int[] nums, int target) {dfs(nums,target,0,0);return ret;}// pos 表示当前针对 nums[pos] 进行操作public void dfs(int[] nums,int target,int pos,int sum){// 递归出口if(pos == nums.length){if(sum == target){ret++;}return;}// 加dfs(nums,target,pos+1,sum+nums[pos]);// 减dfs(nums,target,pos+1,sum-nums[pos]);}
}

(当全局变量是一个数组类型，比如int[]，这种就适合全局变量引入，比如全排列那种类型的题目；而如果全局变量是一个整形类型或者一个单独的类型的时候，则考虑参数引入更合适一些，不需要手动去处理回溯)