离散数学例题——4.计数和集合论（特殊关系、计数基础和函数）

等价关系

在这里插入图片描述

等价关系的证明

在这里插入图片描述
在这里插入图片描述

等价类和商集

在这里插入图片描述
在这里插入图片描述

等价关系与划分一一对应

在这里插入图片描述

偏序关系

在这里插入图片描述

证明偏序关系

在这里插入图片描述

哈斯图

在这里插入图片描述

整除关系画哈斯图

在这里插入图片描述
在这里插入图片描述

特殊元素

最大最小元，极大极小元

在这里插入图片描述

上界上确界，下界下确界

在这里插入图片描述
在这里插入图片描述

其他关系

全序关系、良序关系

在这里插入图片描述

拟序关系、相容关系

在这里插入图片描述

计数基础

在这里插入图片描述
在这里插入图片描述

排列组合

在这里插入图片描述

函数定义

在这里插入图片描述

函数的类型

在这里插入图片描述

函数类型证明

在这里插入图片描述
在这里插入图片描述

构造单射函数证明集合的基数大小比较

在这里插入图片描述

函数复合运算

在这里插入图片描述

函数逆运算

在这里插入图片描述

函数运算的保守性

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.rhkb.cn/news/271230.html

如若内容造成侵权/违法违规/事实不符，请联系长河编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

Chromium内核浏览器编译记（四）Linux版本CEF编译

Chromium内核浏览器编译记（四）Linux版本CEF编译

转载请注明出处：https://blog.csdn.net/kong_gu_you_lan/article/details/136508294 本文出自 容华谢后的博客 0.写在前面 本篇文章是用来记录编译Linux版本CEF的步骤和踩过的坑，以防止后续再用到的时候忘记，同时也希望能够帮助到遇到同样问…
阅读更多...
离散数学例题——5.图论基础

离散数学例题——5.图论基础

基本的图 关联矩阵 子图和补图 度数和握手定理 注意！！！无向图的度数，要行/列和对角线值 根据度数序列判定是否为无向图 度和握手定理证明题 竞赛图 同构图 自补图 通路和回路数量 通路和回路数量 最短路径——dijkstra算法 连通…
阅读更多...
[数据结构初阶]队列

[数据结构初阶]队列

鼠鼠我呀，今天写一个基于C语言关于队列的博客，如果有兴趣的读者老爷可以抽空看看，很希望的到各位老爷观点和点评捏！ 在此今日，也祝各位小姐姐女生节快乐啊，愿笑容依旧灿烂如初阳，勇气与童真永不…
阅读更多...
【HTML】HTML基础7.2（有序列表）

【HTML】HTML基础7.2（有序列表）

目录 标签 效果 注意 标签 <ol> <li>列表内容</li> <li>列表内容</li> <li>列表内容</li> <li>列表内容</li> 。。。。。。 </ol> 效果 代码 <ol><li>银河护卫队 10000000000</li><l…
阅读更多...
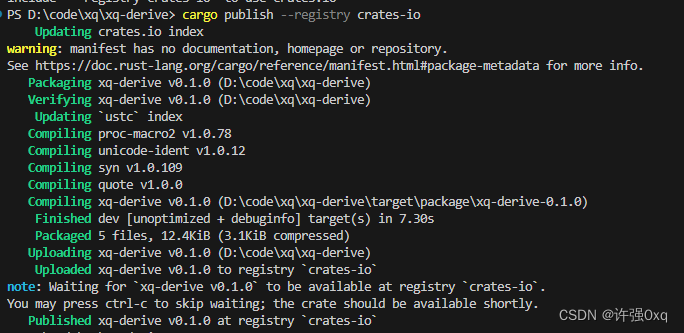
RUST 每日一省：发布到crates.io

RUST 每日一省：发布到crates.io

github是开源代码分享的地方&#xff0c;rust的开源项目除了github&#xff0c;我们还可以将其发布到 crates.io 上&#xff0c;然后其它用户就可以使用cargo进行安装使用了。其实步骤很简单&#xff0c;只有三条命令了&#xff0c;我们一次来看一下。 1、cargo package 首先&a…
阅读更多...
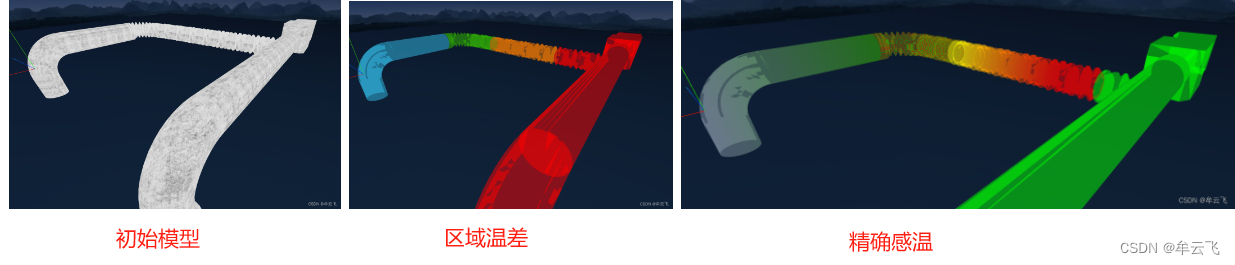
Threejs着色器(GPU)编程——感温管网

Threejs着色器(GPU)编程——感温管网

管网，作为支撑现代城市运转的重要基础设施，是隐藏在地面之下的庞大工程网络。这些管网如同城市的血脉，负责输送各种必要的资源，如水源、热力、燃气等，同时排除废水和其他废弃物。然而，由于其位于地下，人们往往难以直接感知其存在和运行状态。为了保障这些地下管网的安全…
阅读更多...
Go编程实战：高效利用encoding/binary进行数据编解码

Go编程实战：高效利用encoding/binary进行数据编解码

Go编程实战&#xff1a;高效利用encoding/binary进行数据编解码 引言encoding/binary 包核心概念ByteOrder 接口Binary 数据类型的处理处理复杂数据结构 基础使用教程数据类型与二进制格式的映射基本读写操作写操作 - binary.Write读操作 - binary.Read 错误处理 高级功能与技巧…
阅读更多...
手机备忘录可以设置密码吗 能锁屏加密的备忘录

手机备忘录可以设置密码吗 能锁屏加密的备忘录

在繁忙的生活中&#xff0c;手机备忘录成了我随身携带的“小秘书”。那些关于工作的灵感、生活的琐事&#xff0c;甚至深藏心底的小秘密&#xff0c;都被我一一记录在里面。然而&#xff0c;每次当手机离开我的视线&#xff0c;或者需要借给他人使用时&#xff0c;我总会心生担…
阅读更多...
Vue+SpringBoot打造校园疫情防控管理系统

Vue+SpringBoot打造校园疫情防控管理系统

目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 学生2.2 老师2.3 学校管理部门 三、系统展示四、核心代码4.1 新增健康情况上报4.2 查询健康咨询4.3 新增离返校申请4.4 查询防疫物资4.5 查询防控宣传数据 五、免责说明 一、摘要 1.1 项目介绍 基于JAVAVueSpringBoot…
阅读更多...
力扣刷题Days12第二题--100相同的树（js）

力扣刷题Days12第二题--100相同的树（js）

目录 1,题目 2&#xff0c;代码 2.1深度优先遍历 2.2广度优先遍历 3&#xff0c;学习与总结 1,题目 给你两棵二叉树的根节点 p 和 q &#xff0c;编写一个函数来检验这两棵树是否相同。 如果两个树在结构上相同&#xff0c;并且节点具有相同的值&#xff0c;则认为它们是…
阅读更多...
数字孪生10个技术栈：数据处理的六步骤，以获得可靠数据。

数字孪生10个技术栈：数据处理的六步骤，以获得可靠数据。

一、什么是数据处理 在数字孪生中&#xff0c;数据处理是指对采集到的实时或历史数据进行整理、清洗、分析和转化的过程。数据处理是数字孪生的基础&#xff0c;它将原始数据转化为有意义的信息&#xff0c;用于模型构建、仿真和决策支持。 数据处理是为了提高数据质量、整合数…
阅读更多...
ElasticSearch之通过search after和scroll解决深度分页问题

ElasticSearch之通过search after和scroll解决深度分页问题

写在前面 通过from&#xff0c;size来进行分页查询时&#xff0c;如下&#xff1a; 当from比较大时会有深度分页问题&#xff0c;问题产生的核心是coordinate node需要从每个分片中获取fromsize条数据&#xff0c;当from比较大&#xff0c;整体需要获取的数据量也会比较大&am…
阅读更多...
阿珊解析Vuex：实现状态管理的利器

阿珊解析Vuex：实现状态管理的利器

&#x1f90d; 前端开发工程师、技术日更博主、已过CET6 &#x1f368; 阿珊和她的猫_CSDN博客专家、23年度博客之星前端领域TOP1 &#x1f560; 牛客高级专题作者、打造专栏《前端面试必备》 、《2024面试高频手撕题》 &#x1f35a; 蓝桥云课签约作者、上架课程《Vue.js 和 E…
阅读更多...
[c++] c++ 中的顺序(构造，析构，初始化列表，继承)

[c++] c++ 中的顺序(构造，析构，初始化列表，继承)

对象构造的时候&#xff0c;对象成员变量的初始化顺序是什么样的 &#xff1f; 派生类构造的时候&#xff0c;先构造基类还是先构造派生类 &#xff1f; 构造函数中的初始化列表&#xff0c;初始化的顺序是列表的顺序吗 &#xff1f; 析构的时候&#xff0c;析构的顺序是什么…
阅读更多...
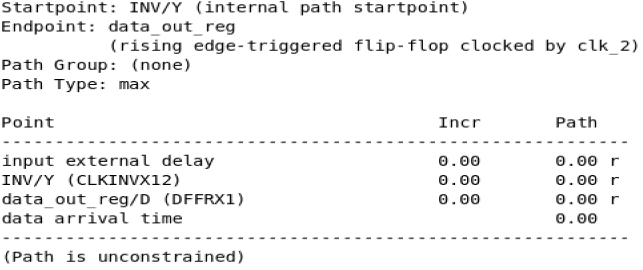
静态时序分析：典型与非典型时序路径的约束详解（一）

静态时序分析：典型与非典型时序路径的约束详解（一）

相关阅读 静态时序分析https://blog.csdn.net/weixin_45791458/category_12567571.html?spm1001.2014.3001.5482 时序路径是静态时序分析中的一个重要概念&#xff0c;了解时序路径能帮助设计者更好地编写SDC脚本&#xff0c;本文旨在详细介绍时序路径相关内容。 首先给出时序…
阅读更多...
【重制版】WSDM 2024 2023时空时序论文总结

【重制版】WSDM 2024 2023时空时序论文总结

&#x1f31f;【紧跟前沿】“时空探索之旅”与你一起探索时空奥秘&#xff01;&#x1f680; 欢迎大家关注时空探索之旅 WSDM 2024于2024年3月4日-3月8日在墨西哥梅里达&#xff08;Mrida, Mxico&#xff09;正在举行。目前官网已经放出了所有被录用论文的表单&#xff08;链接…
阅读更多...
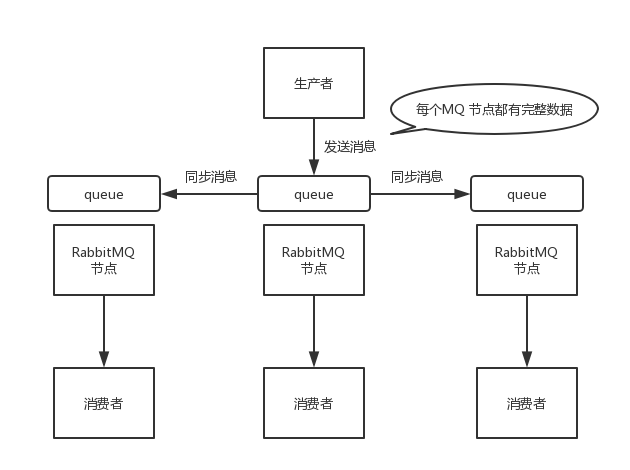
实现消息队列（Kafka、ActiveMQ、RabbitMQ和RocketMQ）高可用

实现消息队列（Kafka、ActiveMQ、RabbitMQ和RocketMQ）高可用

概述 单机没有高可用可言&#xff0c;高可用都对集群来说的 要保证消息队列系统&#xff08;如Kafka、ActiveMQ、RabbitMQ和RocketMQ&#xff09;的高可用性&#xff0c;可以采取以下一些通用的措施&#xff1a; 集群部署&#xff1a;将消息队列系统部署为集群&#xff0c;包…
阅读更多...
uniapp和vue项目配置多语言，实现前端切换语言

uniapp和vue项目配置多语言，实现前端切换语言

在uniapp中配置多语言功能&#xff0c;实现前端切换语言&#xff0c;可以按照以下步骤进行&#xff1a; 1. 创建语言包 首先&#xff0c;创建一个名为 lang 的目录&#xff0c;并在该目录下为每种支持的语言创建对应的JSON或JS文件。例如&#xff1a; lang/en.js&#xff08…
阅读更多...
【Linux】深入理解cd命令

【Linux】深入理解cd命令

&#x1f34e;个人博客&#xff1a;个人主页 &#x1f3c6;个人专栏&#xff1a;Linux ⛳️ 功不唐捐&#xff0c;玉汝于成 目录 前言 正文 基本用法&#xff1a; 相对路径和绝对路径&#xff1a; 特殊符号和快捷方式&#xff1a; 符号链接&#xff1a; 自动补全&…
阅读更多...
重装系统后正版office如何安装

重装系统后正版office如何安装

前言 重装系统后&#xff0c;正版office如何安装 登录官网 https://www.microsoft.com 下载office https://account.microsoft.com/services
阅读更多...
最新文章
推荐文章

Copyright @ 2022~2023