docker
1、官网下载docker文件Get Started | Docker,选择download for windows下载。
2、双击打开下载好的文件Docker Desktop Installer.exe,add shortcut to desktop选择√代表同意添加快捷键到桌面,如果不勾选就说明不创建快捷键,大家根据自己需求选择就行。之后点击🆗
3、等待一会后会出现下图所示,1说明安装成功,2说明必须重启电脑才能成功安装,3代表关闭这个界面重启电脑
4、重启电脑后,会弹出如下界面,如果选择了accept,就会同意1、Docker订阅服务协议;2、Docker 服务的数据处理协议;3、Docker 隐私。同意就好了(DDDD懂的都懂)
5、accept之后报如下错must be BIOS,这说明需要启动本机虚拟机管理程序Hyper-V。
6、找到控制面板--程序--程序和功能--启用或关闭windows功能 ,勾选Hyper-V。
7、也可以输入下述命令在Windows 操作系统中启用 Microsoft Hyper-V 虚拟化技术。
dism.exe /Online /Enable-Feature:Microsoft-Hyper-V /All8、然后输入下述命令,设置 Windows 操作系统中的 Hyper-V 启动类型。具体来说,它会将 Hypervisor 的启动类型设置为 "auto",这意味着在系统启动时自动启动 Hyper-V。
bcdedit /set hypervisorlaunchtype auto8.1、 如果你的系统跟我一样是window11家庭中文版,则会找不到Hyper-Vr,这时则需要自己创建,讲下述代码复制在txt文本里,并重命名为Hyper.cmd,![]() ,右键以管理员方式运行,最后输入“Y”重启电脑后即可。
,右键以管理员方式运行,最后输入“Y”重启电脑后即可。
pushd "%~dp0"
dir /b %SystemRoot%\servicing\Packages\*Hyper-V*.mum >hyper-v.txt
for /f %%i in ('findstr /i . hyper-v.txt 2^>nul') do dism /online /norestart /add-package:"%SystemRoot%\servicing\Packages\%%i"
del hyper-v.txt
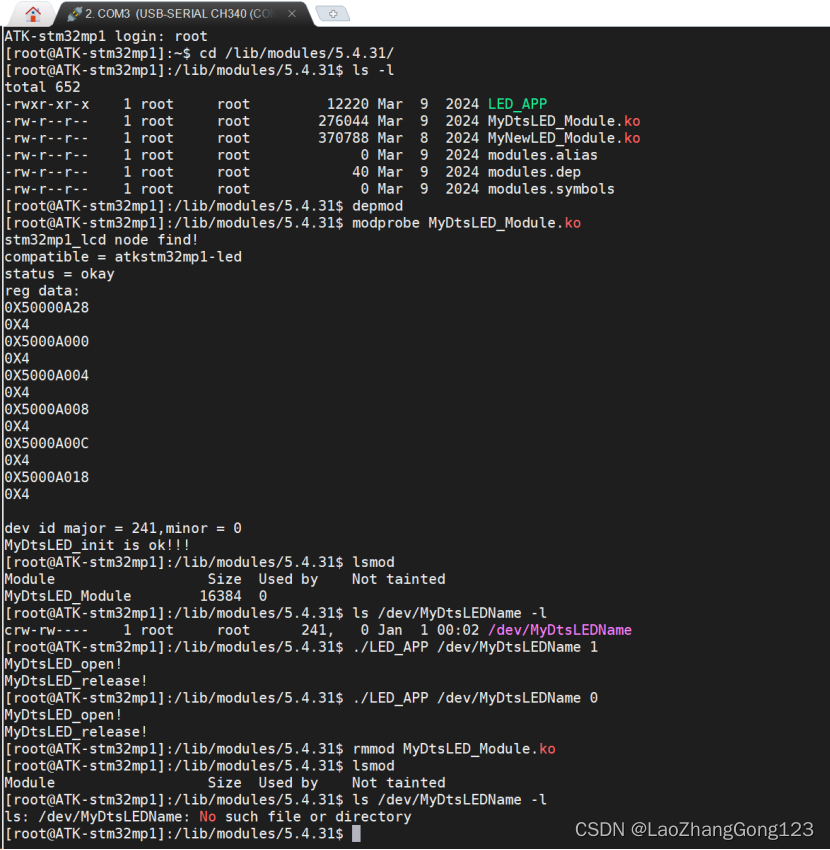
Dism /online /enable-feature /featurename:Microsoft-Hyper-V-All /LimitAccess /ALL11、接着cmd继续输入docker --version检测docker安装的版本,出现如下图说明已经安装docker。
12、继续输入docker run hello-world,出现下图说明docker安装成功,且可以执行docker命令。
13、这时在打开桌面docker快捷键就不会报错了,见下图,此时还能看到hello-world的镜像。
milvus
在cmd某目录下wget
wget https://github.com/milvus-io/milvus/releases/download/v2.0.2/milvus-standalone-docker-compose.yml -O docker-compose.yml去cmd切到对应目录docker compose up -d
查看运行容器
docker compose ps
Milvus单机版启动后,将有三个docker容器在运行,其中包括Milvus独立服务及其两个依赖项。
3、停止Milvus
要停止Milvus单机版,运行:
sudo docker-compose down安装可视化工具,和数据库装在一起
docker run -p 8000:3000 -e MILVUS_URL=127.0.0.1:19530 zilliz/attu:latest
我用chrome打不开下面 用的edge打开
http://localhost:8000/#/connect点击连接之后报错:Error: 14 UNAVAILABLE: No connection established
docker ps -a
docker stop <attu容器ID>
docker rm <attu容器ID>
docker stop 556838c87579
docker rm 556838c87579
改成自己ip不要用 127.0.0.1
docker run -p 8000:3000 -e MILVUS_URL=10.67.68.127:19530 zilliz/attu:latest
milvus is not ready yet
rm -rf volumes
windows是del volumes
python下载pymivlus时要和数据库版本一致 不然
this version of sdk is incompatible with server, please downgrade your sdk or upgrade your server