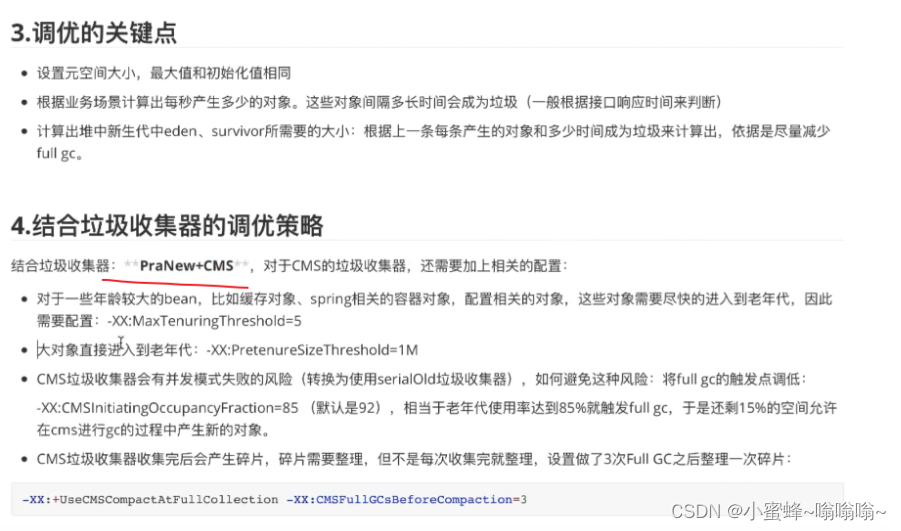
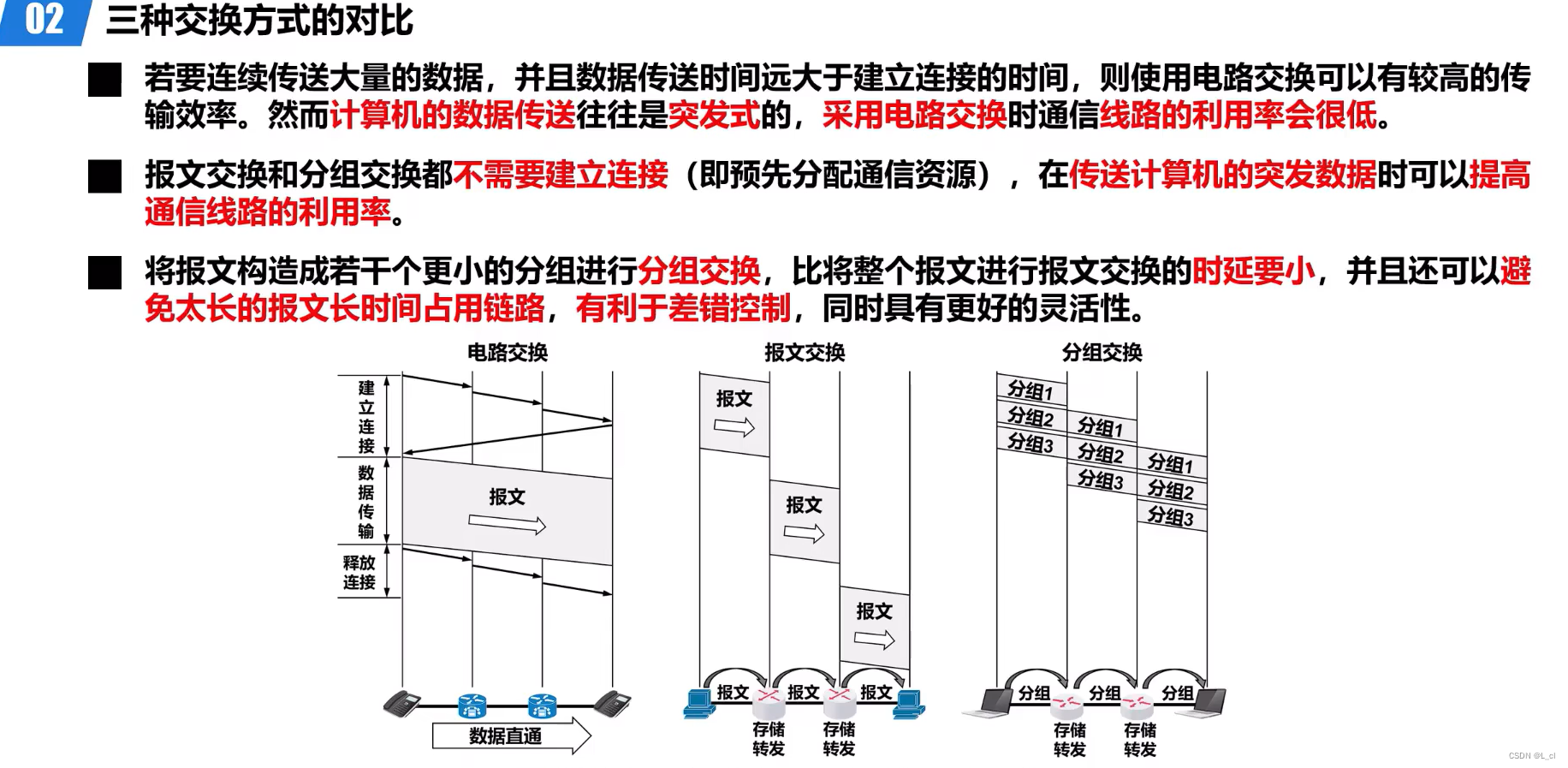
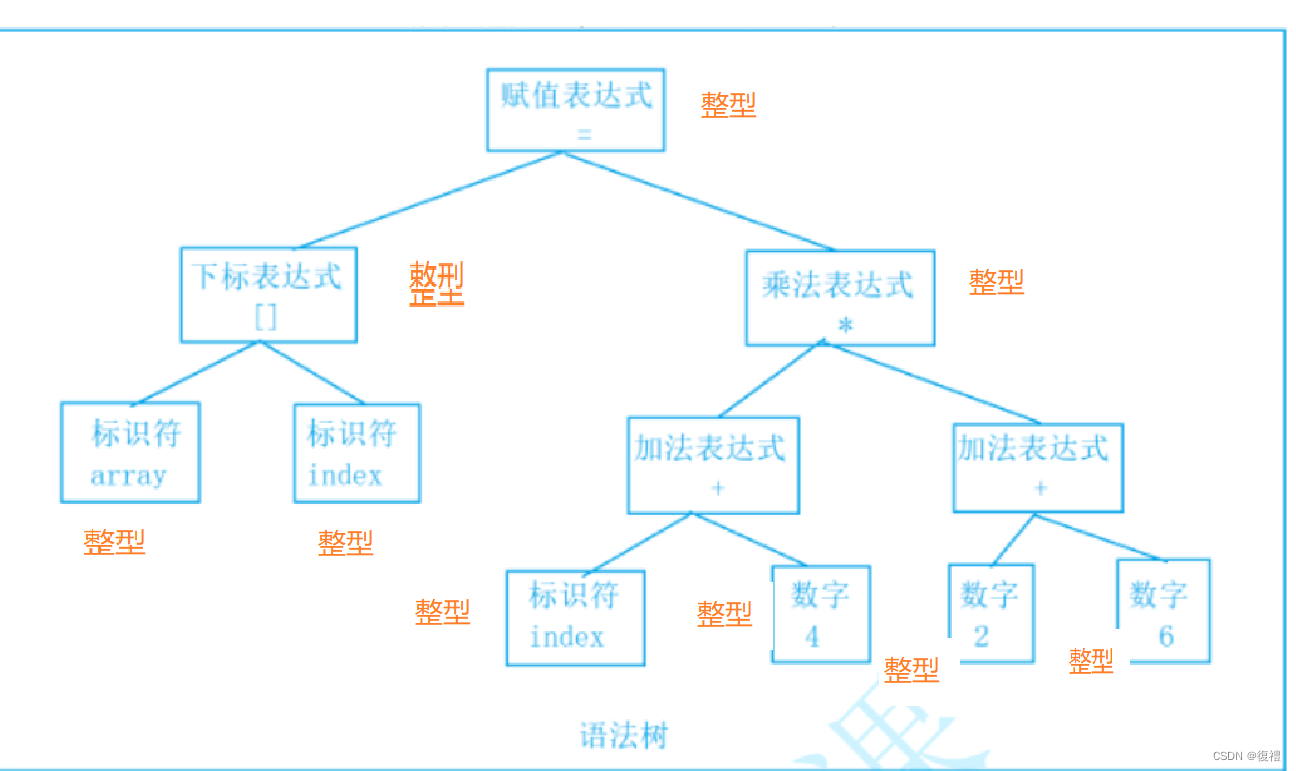
前面的文章我们练习数十道 动态规划 的题目。相信小伙伴们对于动态规划的题目已经写的 得心应手 了。
还没看过的小伙伴赶快关注一下,学习如何 秒杀动态规划 吧!
接下来我们开启一个新的篇章 —— 「滑动窗口」。
滑动窗口
滑动窗口 是一种基于 双指针 思想的算法。两个指针指向的元素之间会形成一个窗口,从前往后遍历元素进行一定的运算。

从名字中也不难看出:滑动 说明窗口的大小并不是固定不变的。通过左右指针按照 规则 向前滑动形成的不同大小的窗口解决具体的问题。
因此,分析问题的 关键 就在于 明确两个指针的移动规则 。
核心步骤
-
初始时,
L = R = 0,并规定窗口的取值为[L, R)即:左闭右开。因此,初始时[0, 0)无意义,窗口内没有任何元素被包含。

-
循环遍历,在保证不会越界的情况下,不断 增大右指针
R。当满足要求后,停止增大右指针R。 -
左指针
L开始 不断增大,直到不满足要求后停下。 -
重复执行 2、3 两步,直到右指针
R走到尽头( 越界 )。
左右指针轮流向前移动,窗口大小不断变化。新旧元素加入和移出后,及时更新该窗口范围内的相关数据。当执行结束后,收集到了所有符合要求的数据,且时间复杂度降低到了 O ( N ) O(N) O(N) 。
下面我们通过一道 力扣 Hard 题 进行学习。
239. 滑动窗口最大值
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。返回 滑动窗口中的 最大值 。

在解决该题目之前,我们先来讨论一下这类题的套路。
思路与套路
对于 窗口内最大最小值 的题目,我们采用 双端队列 的结构进行思考。并对 出队、入队 进行这样的规定(以窗口内的最大值举例):
队列含义:
- 如果此时开始缩窗口(即:L++),哪些值会依次成为此时窗口内的最大值。
- 要求,队列中的元素从大到小排列。
队列的出入:
队尾 的出队与入队:
- 如果队空,直接入队;
- 否则,如果队尾位置不大于当前来到位置的数,从队尾出队。直到队尾元素大于当前位置元素,从队尾入队。
队头 的出队:
- 当窗口缩小时,若队头元素已经不在当前的窗口中时,从队头弹出即可。
是不是没搞懂在说什么,没关系。我们通过具体的例子感受该流程:
就拿例 1 的例子,nums=[1,3,-1,-3,5,3,6,7],构造双端队列的值依次为:
注意: 双端队列中 队头元素 保存的是 当前范围 的 最大值 。
先看从队尾出入队的情况:


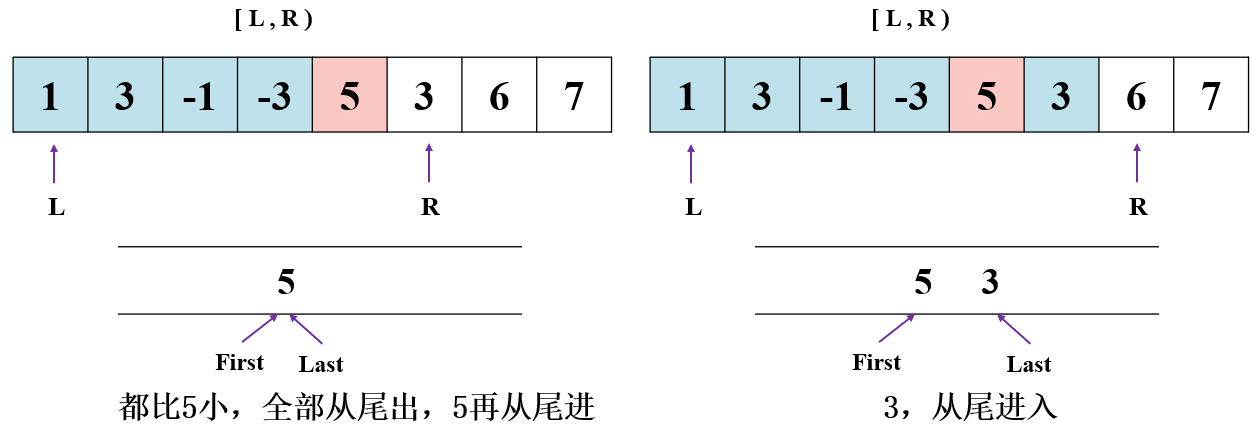
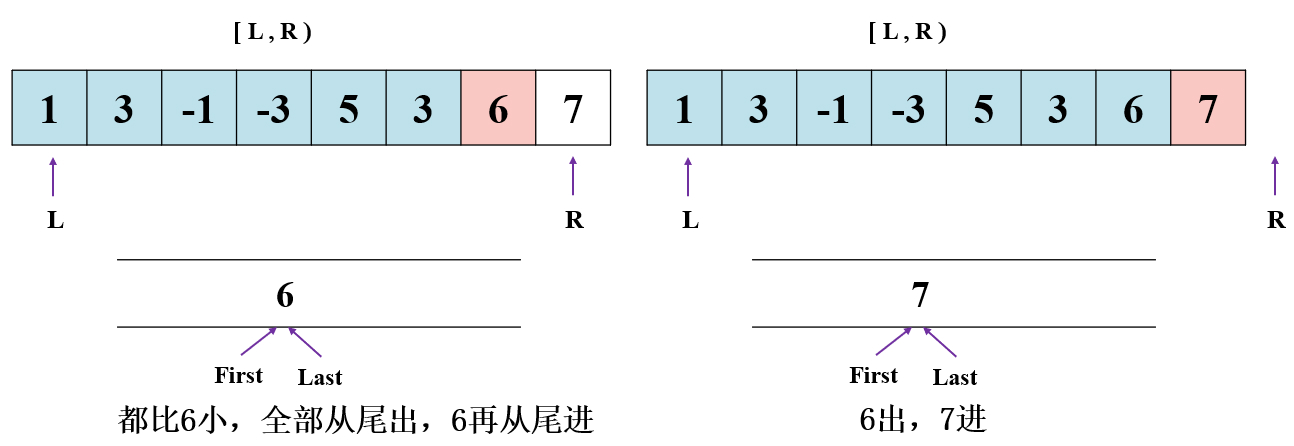
以上均是 L 不动,R 在右移的情况。
再看从队头出队的情况:
下面我们再来看 L 也向右移动的情况:

以 L 指向 1,R 指向 5 时为例:
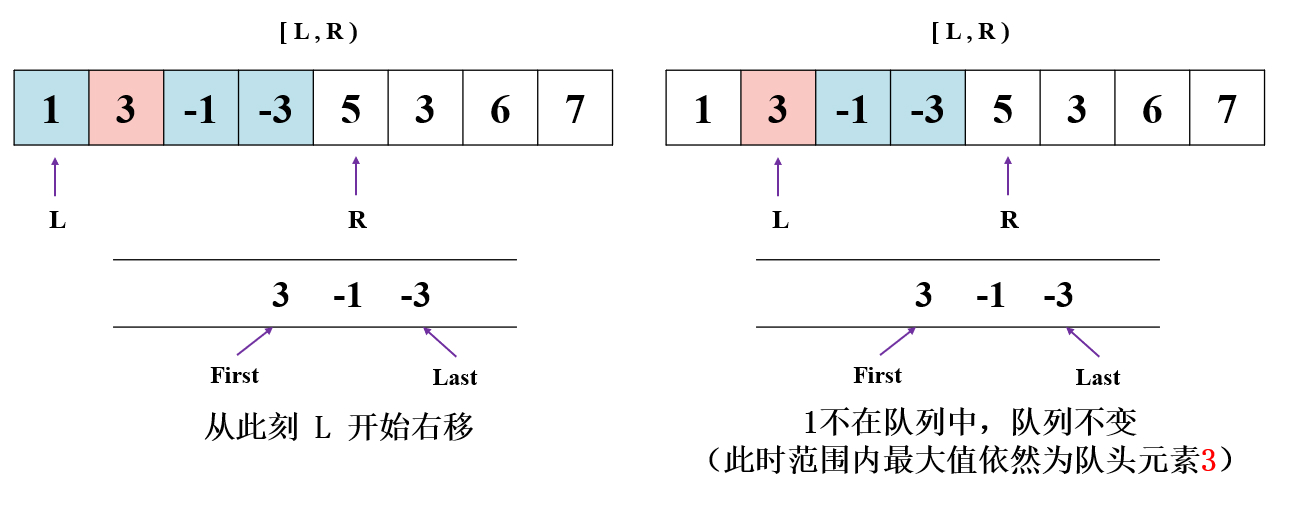

跟着图细心体会该过程哦!相信小伙伴能够理解双端队列的出入规则了!
下面我们回归正题,解决上面力扣 滑动窗口最大值 的题目。
仔细思考后发现,其实就是将上面的过程 加以限制 :
限制了窗口的大小必须为 k 。
直接上代码。
代码
public static int[] getMaxWindow(int[] arr, int w) {if (arr == null || w < 1 || arr.length < w) {return null;}// 双端队列LinkedList<Integer> qmax = new LinkedList<Integer>();int N = arr.length;// 最终会产生 N - w + 1 个结果int[] res = new int[N - w + 1];// res 数组的下标int index = 0;// R 从左到右遍历数组,不回退for (int R = 0; R < N; R++) {// 双端队列中有值,并且 队尾的数 比当前的 小 就弹出while (!qmax.isEmpty() && arr[qmax.peekLast()] <= arr[R]) {qmax.pollLast();}// 双端队列为空,或者弹出完比自己小的数了// 从末尾插入队列中qmax.addLast(R);// R-w 是过期的下标,即 L 的位置// 队头的下标 过期了就弹出if (qmax.peekFirst() == R - w) {qmax.pollFirst();}// 能够形成完整的窗口了,开始往 结果数组 里填最终答案if (R >= w - 1) {res[index++] = arr[qmax.peekFirst()];}}return res;
}
代码解释
其实注释已经写的非常清楚了。
- 在上面的图中,我么在双端队列中放入的是 元素值,但在实际的代码中,存入的是下标,这样的话既能够比较大小,又能方便的进行入队出队操作。
- 窗口大小固定,R 和 L 一起右移。因此若判断出队头元素已经离开了窗口,就要弹出。
- 刚开始,R 从 0 开始增大,窗口还未形成。只有当形成 k 大小的窗口后再开始更新答案。(那 思考一下 为什么不直接从下标 k 开始呢?这不直接就有窗口了么?欢迎留言评论 ~)
~ 点赞 ~ 关注 ~ 星标 ~ 不迷路 ~!!!
关注回复「ACM紫书」获取 ACM 算法书籍~