1.导数、偏微分、梯度

1.1 导数

对于y=x$2$ 的导数，描述了y随x值变化的一个变化趋势，导数是个标量反应的是变化的程度，标量的长度反应变化率的大小。

1.2 偏微分

偏微分是函数对它的自变量变化率的描述程度，也是标量，是给定自变量的方向，有多少个自变量就有多少个偏微分
z = y$2$ + x$2$
求z对y的偏微分时，把x看成常量

1.3 梯度

梯度是函数所有自变量偏微分组成的向量，梯度既有大小又有方向，大小表示函数在当前点的一个增长速率，方向表示函数在当前点的一个增长方向。

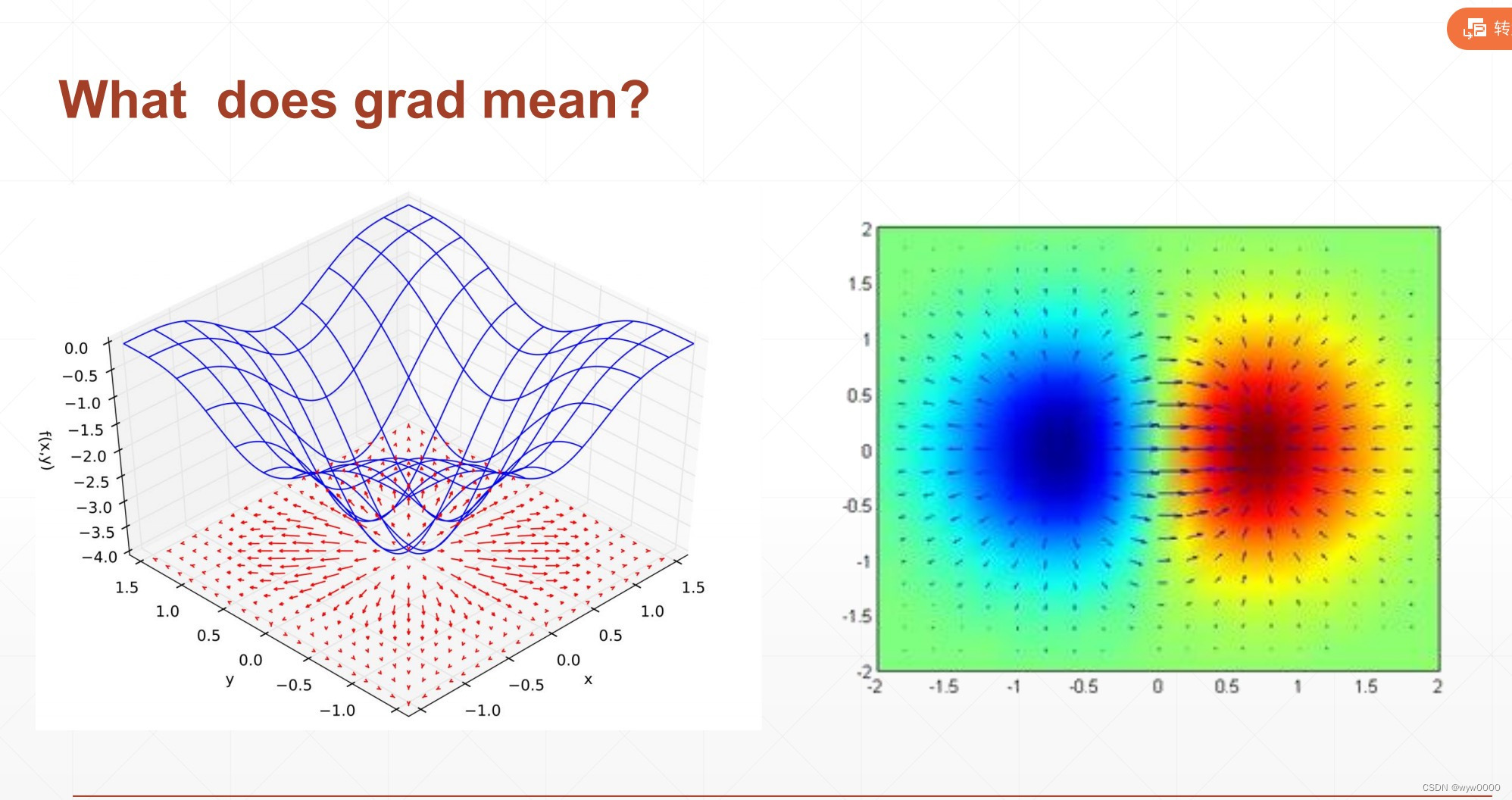
2. 通过梯度求极小值

如下例子：

上述例子中的function相当于z=x$2$+y$2$，z对x求导时，y看成常数因此导数为0，同样z对y求导时，x看成常数，因此导数为0。

3. learning rate

为了使梯度变化不至于太快，还要再y’上乘以一个learning rate即学习率

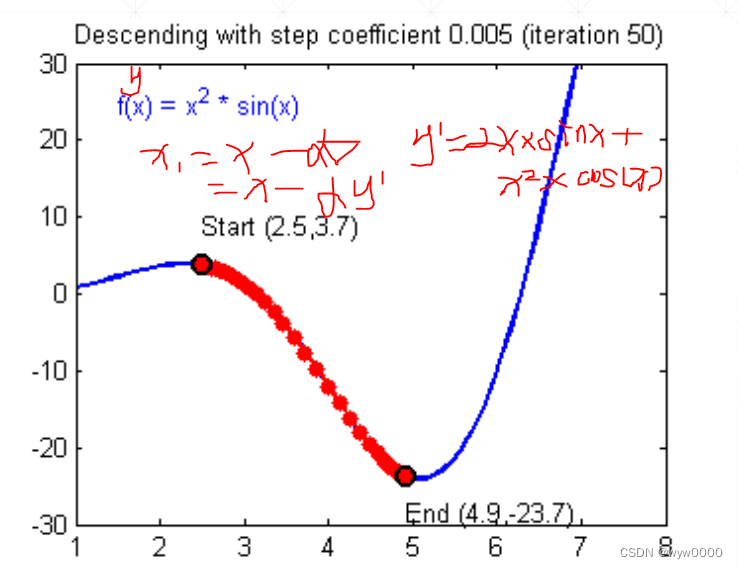
3. 局部最小值

如下图：从不同的初始化方向，可能找到的是局部最小值，比如从图中箭头方向搜索。

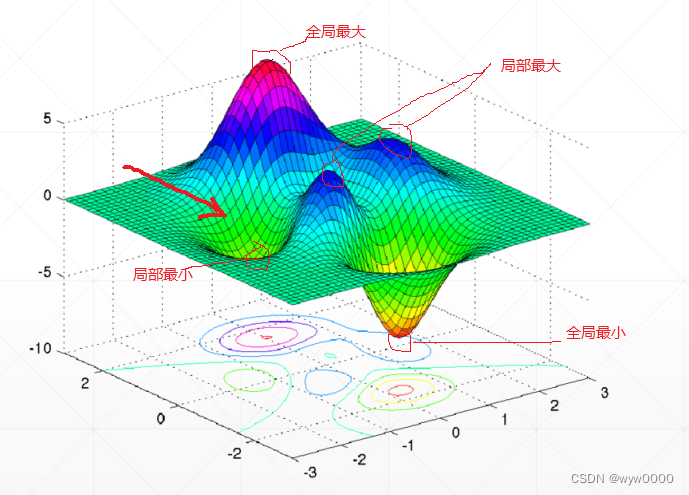
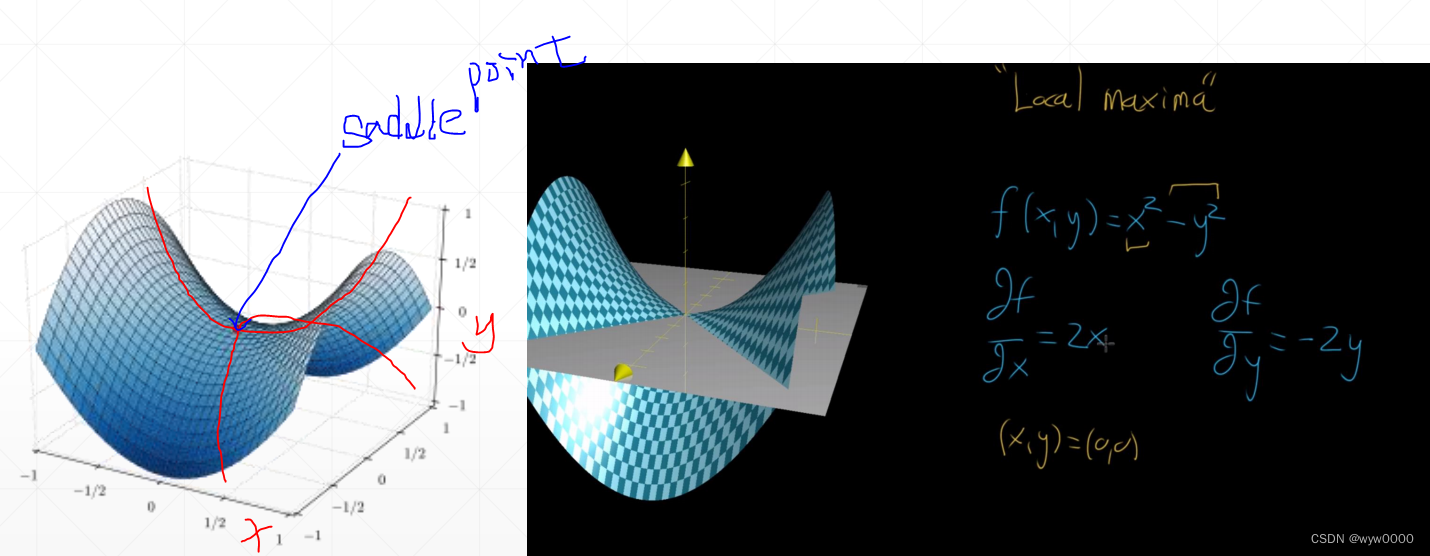
4. Saddle point鞍点

如下图：指示的点即为鞍点，像马鞍一样，此时x方向取得最小值，y方向取得最大值