前言

在关键字排列随机的情况下，二叉排序树的平均查找长度和$logn$是等数量级的。在某些情况下，尚需在构成二叉排序树的过程中进行“平衡化”处理，使其成为平衡二叉树。
如果任何初始化序列构成的二叉排序树都是平衡二叉树，因为平衡二叉树上任何结点的左右子树的深度之差都不超过1，则可以证明它的深度和$logn$是同数量级别的(其中n为结点个数)。由此，它的平均查找长度也和$logn$同数量级。

平衡二叉树定义及性质

平衡二叉树(Balanced Binary Tree 或 Height-Balanced Tree)又称AVL树。它或者是一棵空树，或者是具有下列性质的二叉树：
(1) 它的左子树和右子树都是平衡二叉树；
(2) 它的左子树和右子树的深度之差的绝对值不超过1。若将二叉树上结点的平衡因子定位为该结点的左子树的深度减去它的右子树的深度，则平衡二叉树上所有节点的平衡因子只可能是-1、0和1。

平衡二叉排序树的插入操作

一般情况下，假设由于在二叉排序树上插入结点而失去平衡的最小树根结点的指针为a(即a是离插入结点最近，且平衡因子绝对值超过1的祖先节点)，则失去平衡后进行调整的规律可归纳为下列4种情况：
(1) 单向右旋平衡处理：由于在*a的左子树根结点的左子树上插入结点，*a的平衡因子由1增至2，致使以*a为根的子树失去平衡，则需再进行一次向右的顺时针旋转操作。如下图所示：

(2) 单向左旋平衡处理：由于在*a的右子树根结点的右子树上插入结点，*a的平衡因子由-1增至-2，致使以*a为根的子树失去平衡，则需再进行一次向左的逆时针旋转操作。如下图所示：

(3) 双向旋转(先左后右)平衡处理：由于在*a的左子树根结点的右子树上插入结点，*a的平衡因子由1增至2，致使以*a为根结点的子树失去平衡，则需进行两次旋转(先左旋后右旋)操作。如下图所示：

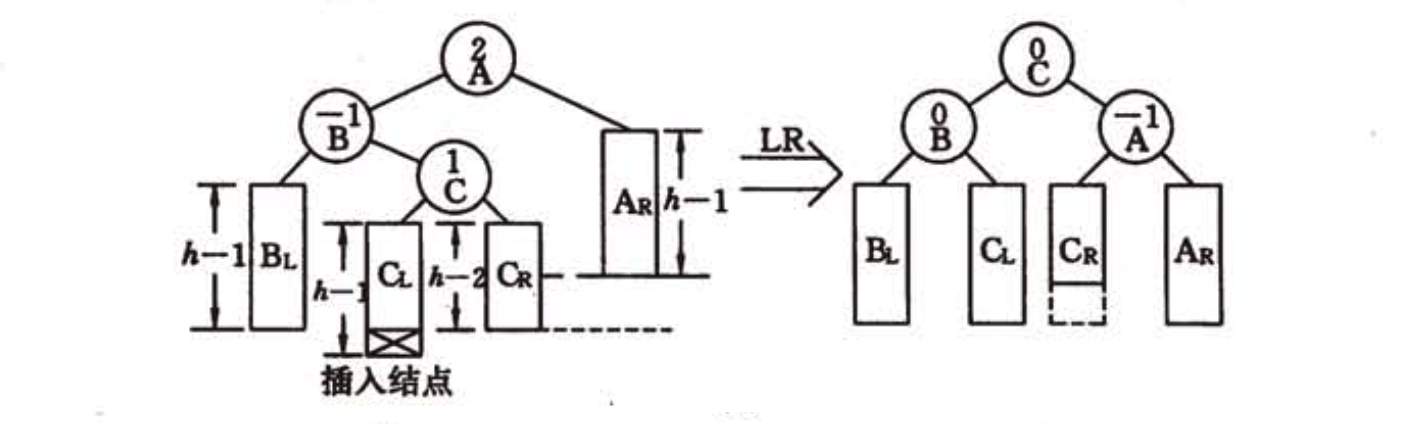
(4) 双向旋转(先右后左)平衡处理：由于在*a的右子树根结点的左子树上插入结点，*a的平衡因子由-1增至-2，致使以*a为根结点的子树失去平衡，则需进行两次旋转(先右旋后左旋)操作。如下图所示：

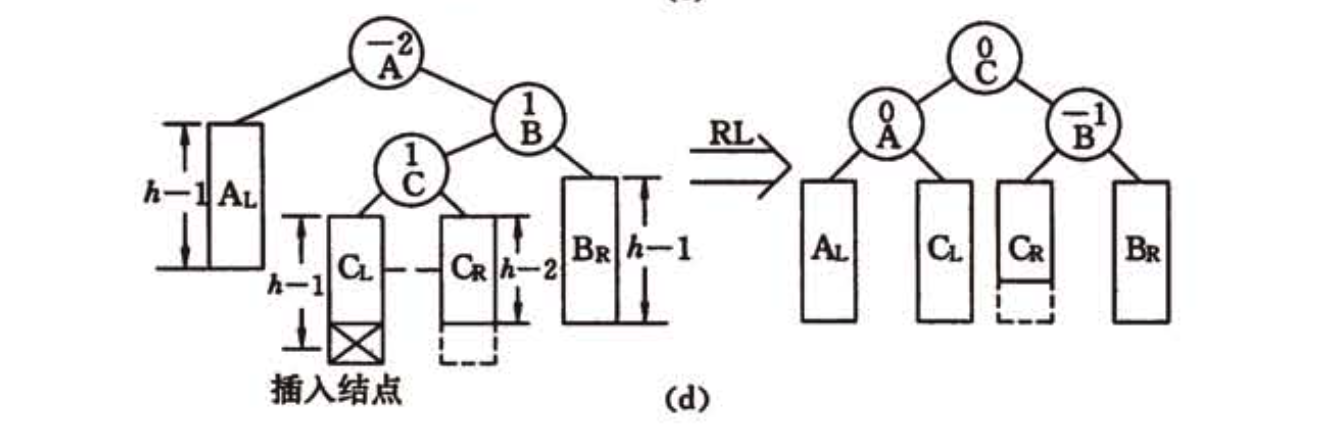
上述4中情况，(1)和(2)对称，(3)和(4)对称。旋转操作的正确性容易由"保持二叉排序树的特性：中序遍历所得关键字序列由小至大有序"证明。当平衡的二叉排序树因插入结点而失去平衡时，仅需对最小不平衡子树进行旋转即可。因为经过旋转处理之后的子树深度和插入之前相同，因而不影响插入路径上所有祖先结点的平衡度。
在平衡的二叉排序树BBST上插入一个新的数据元素e的递归算法可描述如下：
(1) 若BBST为空树，则插入一个数据元素为e的新结点作为BBST的根结点，树的深度加1。
(2) 若e的关键字和BBST的根结点的关键字相等，则不进行插入。
(3) 若e的关键字小于BBST的根结点的关键字，而且在BBST的左子树中不存在和e有相同关键字的结点，则将e插入在BBST的左子树上，并且当插入之后的左子树深度+1时，分别就下列不同情况处理之：
(a) BBST的根结点的平衡因子为-1(右子树的深度大于左子树的深度)：则将根结点的平衡因子更改为0，BBST的深度不变；
(b) BBST的根结点的平衡因子为0(左子树和右子树的深度相等)：则将根结点的平衡因子更改为1，BBST的深度+1；
© BBST的根结点的平衡因子为1(左子树的深度大于右子树的深度：若BBST的左子树根结点的平衡因子为1，则需进行单向右旋平衡处理，并且在右旋后，将根结点和其右子树根结点的平衡因子更改为0，树的深度不变；若BBST的左子树根结点的平衡因子为-1，则需进行先向左、后向右的双向旋转平衡处理，并且在旋转处理之后，修改根结点和其左子树、右子树根结点的平衡因子，树的深度不变；
(4) 若e的关键字大于BBST的根结点的关键字，而且在BBST的右子树不存在于e有相同关键字的结点，则将e插入在BBST的右子树上，并且当插入之后的右子树深度+1时，分别就不同的情况处理之。其处理操作和步骤3中所述相对称，这里不展开说明。
由于平衡二叉排序树的插入代码实现较复杂，有兴趣的同学可以自行参考**《数据结构》的9.2.1 二叉排序树和平衡二叉树小节**学习。

平衡二叉排序树的创建

将二叉排序树转换成平衡树

public TreeNode balanceBST(TreeNode root) {List<Integer> sortedList = new ArrayList();traverseByInorder(root, sortedList);return createTree(sortedList, 0, sortedList.size()-1);
}private void traverseByInorder(TreeNode root, List<Integer> sortedList) {if(root == null) {return;}traverseByInorder(root.left, sortedList);sortedList.add(root.val);traverseByInorder(root.right, sortedList);
}private TreeNode createTree(List<Integer> sortedList, int left, int right) {int mid = (left + right) >> 1;TreeNode root = new TreeNode(sortedList.get(mid));if(left <= mid -1) {root.left = createTree(sortedList, left, mid -1);}if(right >= mid+1) {root.right = createTree(sortedList, mid+1, right);}return root;
}

将有序数组转换平衡二叉排序树

public TreeNode sortedArrayToBST(int[] nums) {return createTree(nums, 0, nums.length - 1);
}private TreeNode createTree(int[] nums, int left, int right) {if(nums.length == 0) {return null;}int mid = (left + right) >> 1;TreeNode root = new TreeNode(nums[mid]);if(left<= mid -1) {root.left = createTree(nums, left, mid - 1);}if(right>= mid +1) {root.right = createTree(nums, mid +1, right);}return root;
}

将有序链表转换成平衡二叉排序树

public TreeNode sortedListToBST(ListNode head) {return createTree(head, null);
}private TreeNode createTree(ListNode leftNode, ListNode rightNode) {if(leftNode == rightNode) {return null;}ListNode middleNode = getMiddleNode(leftNode, rightNode);TreeNode root = new TreeNode(middleNode.val);root.left = createTree(leftNode, middleNode);root.right = createTree(middleNode.next, rightNode);return root;
}private ListNode getMiddleNode(ListNode left, ListNode right) {ListNode fast = left;ListNode slow = left;while (fast != right && fast.next != right) {fast = fast.next.next;slow = slow.next;}return slow;
}

判断一棵树是否是平衡二叉树

判断一棵树是不是平衡二叉树，就是判断这棵树是否满足平衡二叉树的性质：
(1) 它的左子树和右子树都是平衡二叉树；
(2) 它的左子树和右子树的深度之差的绝对值不超过1。若将二叉树上结点的平衡因子定位为该结点的左子树的深度减去它的右子树的深度，则平衡二叉树上所有节点的平衡因子只可能是-1、0和1。

public boolean isBalanced(TreeNode root) {if(root == null) {return true;}return Math.abs(height(root.left) - height(root.right))<=1 && isBalanced(root.left) && isBalanced(root.right);
}private int height(TreeNode root) {if(root == null) {return 0;}return Math.max(height(root.left), height(root.right)) + 1;
}

public boolean isBalanced(TreeNode root) {return height(root) >= 0;
}
private int height(TreeNode root) {if(root == null) {return 0;}int leftHeight = height(root.left);int rightHeight = height(root.right);if(leftHeight == -1 || rightHeight == -1 || Math.abs(leftHeight - rightHeight) > 1) {return -1;}return Math.max(leftHeight, rightHeight) + 1;
}

参考

《数据结构》 严蔚敏 吴伟民 著 9.2.1 二叉排序树和平衡二叉树
https://zhuanlan.zhihu.com/p/163515903 平衡二叉树专题
https://leetcode.cn/problems/convert-sorted-array-to-binary-search-tree/ 108. 将有序数组转换为高度平衡的二叉搜索树
https://leetcode.cn/problems/convert-sorted-list-to-binary-search-tree/ 109. 有序链表转换为高度平衡的二叉搜索树
https://leetcode.cn/problems/balanced-binary-tree/ 110. 平衡二叉树
https://leetcode.cn/problems/balance-a-binary-search-tree/description/ 1382. 将二叉搜索树变平衡的二叉搜索树