深度强化学习（五）（蒙特卡洛与自举）

一.蒙特卡洛与自举

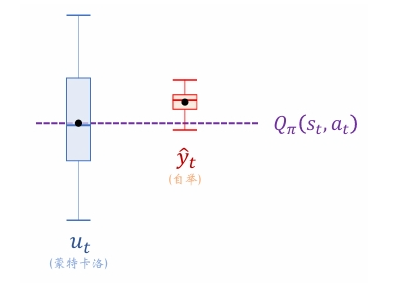
上一节介绍了多步 TD 目标。单步 TD 目标、回报是多步 TD 目标的两种特例。如下图所示, 如果设 $m=1$, 那么多步 TD 目标变成单步 $\mathrm{TD}$ 目标。如果设 $m=n-t+1$, 那么多步 TD 目标变成实际观测的回报 $u_t$ 。

二.蒙特卡洛

我们可以将一局游戏进行到底, 观测到所有的奖励 $r_1,\cdots ,r_n$, 然后计算回报 $u_t={\sum }_{i=0}^{n-t}{\gamma }^i{r}_{t+i}$ 。拿 $u_t$ 作为目标, 鼓励价值网络 $q\left(s_t,a_t;\mathbf{w}\right)$接近 $u_t$ 。定义损失函数:
$$L(\mathbf{w})=\frac{1}{2}{\left[q\left(s_t,a_t;\mathbf{w}\right)-u_t\right]}^2.$$

然后做一次梯度下降更新 $\mathbf{w}$ :
$$\mathbf{w}\leftarrow \mathbf{w}-\alpha \cdot {\nabla }_{\mathbf{w}}L(\mathbf{w}),$$

这样可以让价值网络的预测 $q\left(s_t,a_t;\mathbf{w}\right)$ 更接近 $u_t$ 。这种训练价值网络的方法被称作“蒙特卡洛”

蒙特卡洛的好处是无偏性: $u_t$ 是 $Q_{\pi }\left(s_t,a_t\right)$ 的无偏估计。由于 $u_t$ 的无偏性, 拿 $u_t$ 作为目标训练价值网络, 得到的价值网络也是无偏的。

蒙特卡洛的缺点是方差大。随机变量 $U_t$ 依赖于 $S_{t+1},A_{t+1},\cdots ,S_n,A_n$ 这些随机变量, 其中不确定性很大。观测值 $u_t$ 虽然是 $U_t$ 的无偏估计, 但可能实际上离 $\mathbb{E}\left[U_t\right]$ 很远。因此，拿 $u_t$ 作为目标训练价值网络，收敛会较慢。

三.自举

在强化学习中，“自举”的意思是“用一个估算去更新同类的估算”，。SARSA使用的单步TD目标定义为：
$${\hat{y}}_t=r_t+\underset{\text{价值网络做出的估计 }}{\underbrace{\gamma \cdot q\left(s_{t+1},a_{t+1};\mathbf{w}\right)}}$$
SARSA 鼓励 $q\left(s_t,a_t;\mathbf{w}\right)$ 接近 ${\hat{y}}_t$, 所以定义损失函数
$$L(\mathbf{w})=\frac{1}{2}[\underset{\text{让价值网络拟合 }{\hat{y}}_t}{\underbrace{q\left(s_t,a_t;\mathbf{w}\right)-{\hat{y}}_t}}{]}^2.$$
自举的好处是方差小。单步 TD 目标的随机性只来自于 $S_{t+1}$ 和 $A_{t+1}$, 而回报 $U_t$ 的随机性来自于 $S_{t+1},A_{t+1},\cdots ,S_n,A_n$ 。很显然, 单步 $\mathrm{TD}$ 目标的随机性较小, 因此方差较小。用自举训练价值网络，收敛比较快。

自举的缺点是有偏差。价值网络 $q(s,a;\mathbf{w})$ 是对动作价值 $Q_{\pi }(s,a)$ 的近似。因我们认为${\hat{y}}_t$是真实估计，是一常数，如果本身${\hat{y}}_t$就是有偏差的，则价值网络就会在逼近${\hat{y}}_t$中学习放大这一偏差。

也就是说, 自举会让偏差从 $\left(s_{t+1},a_{t+1}\right)$ 传播到 $\left(s_t,a_t\right)$ 。