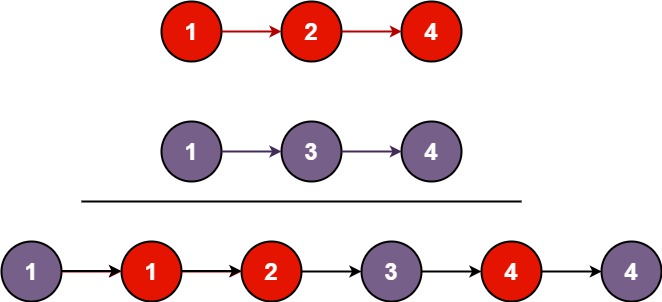
Dijkstra算法的目的是寻找单起点最短路径,其策略是贪心加非负加权队列
一、单起点最短路径问题
单起点最短路径问题:给定一个加权连通图中的特定起点,目标是找出从该起点到图中所有其他顶点的最短路径集合。需要明确的是,这里关心的不仅仅局限于寻找一条从起点出发到任一其他顶点的单一最短路径;单起点最短路径问题要求的是一组路径,每条路径都从起点出发通向图中的一个不同顶点,当然,其中某些路径可能具有公共边。
二、Dijkstra算法原理
Dijkstra算法是一种高效地找出图中从一个给定起点到所有其他顶点最短路径的方法。它按照距离起点的远近顺序,逐步确定到各个顶点的最短路径。具体来说,算法首先找到距离起点最近的顶点,并确定它们之间的最短路径;然后,它接着寻找下一个最近的顶点,依此类推。在第 i i i 次迭代之前,算法已经确定了到达最近的 i − 1 i-1 i−1个顶点的最短路径,这些顶点及其路径构成了原图的一个子图,形成一棵以起点为根的树。
重要的是,由于图中所有边的权重都为非负,算法能够保证每次迭代找到的是当前可达顶点中距离起点最近的一个。这些待选顶点,称为“边缘顶点”,位于已构建的子树的外围。理论上,图中的所有其他顶点也可以被视为边缘顶点,但它们与树中顶点的连接权重被假设为无限大。
为了求出下一个最接近起点的顶点,Dijkstra算法计算每个边缘顶点至其最近的树内顶点的距离(即该边的权重),并将此距离与从起点到该树内顶点的已知最短路径长度相加。在所有这些候选顶点中,算法选择总和最小的顶点作为下一个最近顶点。Dijkstra算法的核心在于,通过仅对这些特定的候选路径进行比较,就可以有效地找到最短路径。
三、Dijkstra算法应用
为了简化算法的实施过程,我们为每个顶点引入两个辅助标记。第一个标记是一个数值标记 d d d,它记录了从算法开始到当前为止,从起点到该顶点的最短路径长度。随着算法的进行,当新的顶点被加入到树中时, d d d 的值更新为从起点到这个新顶点的最短路径长度。第二个标记则记录了该路径上的倒数第二个顶点,即当前构建的树中该顶点的父节点(对于起点以及那些尚未与树中的顶点直接相连的顶点,这个标记不必指定)。有了这两个标记后,寻找下一个最近顶点 u ∗ u^{ *} u∗ 变得相对直接:我们仅需在所有边缘顶点中找到具有最小 d d d 值的顶点即可,而这个查找过程的顺序并不重要。这样,这两个标记极大地简化了算法的步骤,使得确定最短路径的过程更加高效和直观。
在确定了加入树中的顶点u*以后,还需要做两个操作:
-
把 u ∗ u^{ *} u∗ 从边缘集合移到树顶点集合中。
-
对于余下的每一个边缘顶点 u u u,如果通过权重为 w ( u ∗ , u ) w(u^{ *}, u) w(u∗,u) 的边和 u ∗ u^{ *} u∗ 相连,当 d u ∗ + w ( u ∗ , u ) < d u d_{u^{*}} +w(u^{*},u)<d_{u} du∗+w(u∗,u)<du时,把 u u u 的标记分别更新为 u ∗ u^{ *} u∗ 和 d u ∗ + w ( u ∗ , u ) d_{u^{*}} +w(u^{*},u) du∗+w(u∗,u)。

最短的路径(从左列中的目标项点根据非数字标记向起点回溯,来确定最短路径)和它们的长度(由树中数字标记给出)如下:
-
从 a a a 到 b b b : a − b a-b a−b, 长度为3
-
从 a a a 到 d d d : a − b − d a-b-d a−b−d, 长度为5
-
从 a a a 到 c c c ; a − b − c a-b-c a−b−c, 长度为7
-
从 a a a 到 e e e : a − b − d − e a-b-d-e a−b−d−e,长度为9
Dijkstra(G, s)
# 单起点最短路径的Dijkstra算法
# 输入: 带有非负权重的连通图G=<V, E>以及起点顶点s
# 输出: 对于V中的每个顶点v,从s到v的最短路径长度d[v],
# 以及路径上的倒数第二个顶点p[v]Initialize(Q) # 将顶点优先队列初始化为空
for v in V:d[v] ← ∞p[v] ← NoneInsert(Q, v, d[v]) # 初始化优先队列中顶点的优先级d[s] ← 0
Decrease(Q, s, d[s]) # 更新s的优先级为d[s]
p[s] ← Nonefor i from 0 to |V| - 1 do:u ← DeleteMin(Q) # 删除优先级最小的元素for 每一个与u相邻的顶点u' do:if d[u] + w(u, u') < d[u']:d[u'] ← d[u] + w(u, u')p[u'] ← uDecrease(Q, u', d[u'])