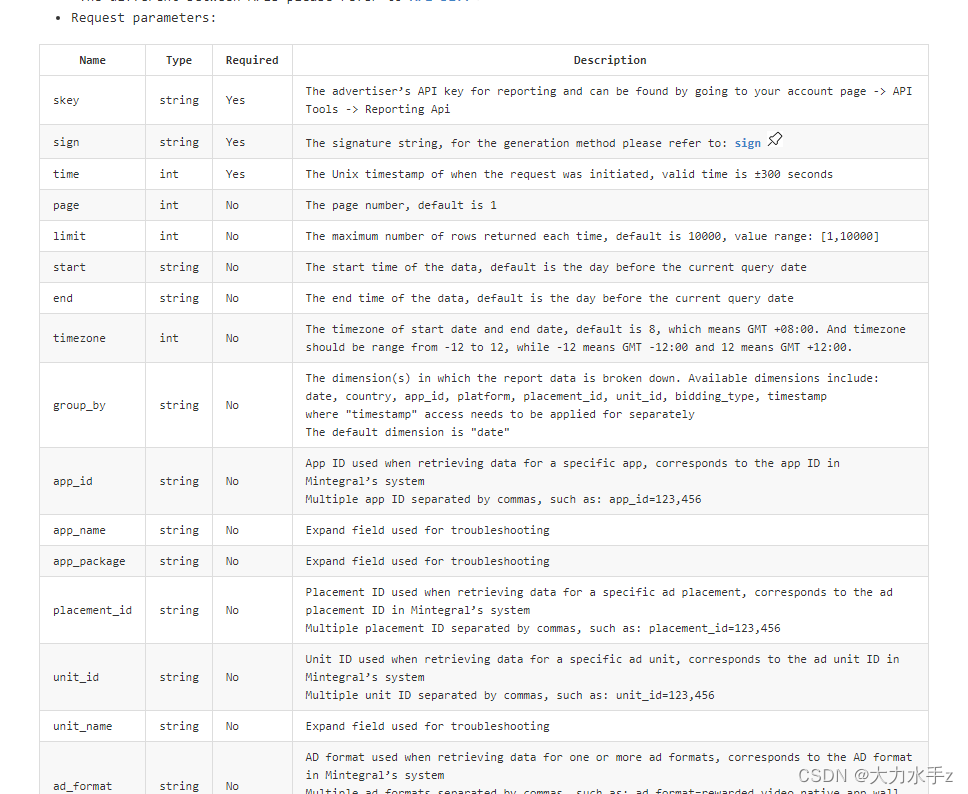
题目
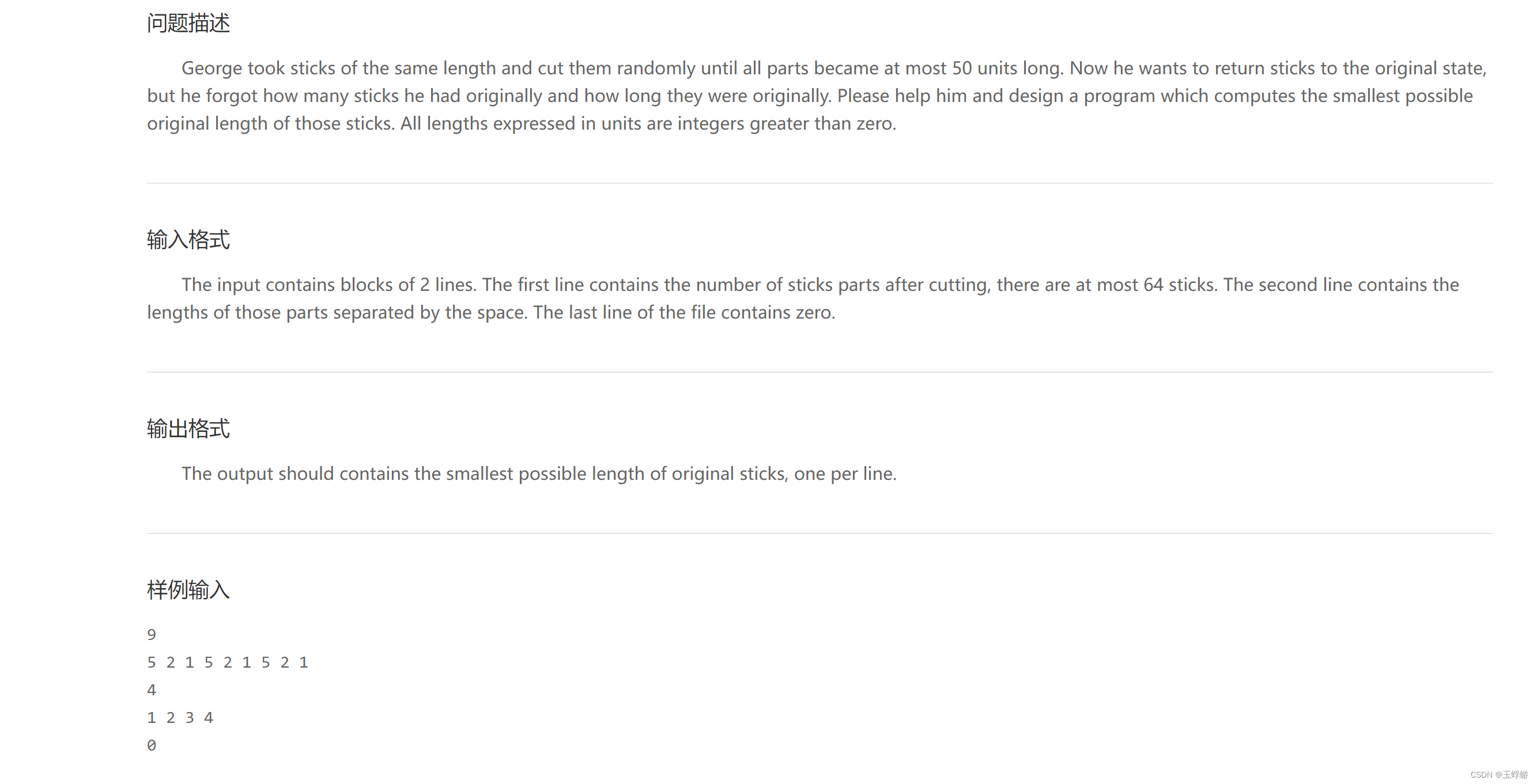
样例输出是
6
5题目中给错了,不知道什么时候会改。
思路
--剪枝,否则时间复杂度和空间复杂度过大,会超时。
--注意有多组测试样例时,需要将bool数组重新赋值为false。
--函数类型不是void,return语句不能省略!
--思路:刚开始想的大方向是对的,将需要处理的数组排序,然后从最大值到总和这个范围内搜索,找满足题意的木棍长度,但是剪枝这里是一头雾水。剪枝是利用一些条件使得不需要dfs许多重复的情况,已经pass掉的就不需要再递归了。看到这一题,很容易联想到粘木棍,将n个短木棍粘成m个长木棍,所不同的是,这里的m个长木棍长度都是相同的。我们可以一根一根来粘,粘成一根长木棍再粘下一根。那么就需要让此时的长木棍的长度作为参数在递归中传递。这时有三种情况,当前长度cur加上选中的短木棍的长度,可能等于、大于、小于目标长度l。(1)如果等于l,开始粘下一根长木棍,长木棍的根数要+1,cur设为0,验证接下来能不能递归成功,如果成功就可以直接返回,如果不成功就返回false,提前结束递归。验证接下来能不能递归成功,就是为了在不成功的情况下提前结束递归。(2)如果大于l,说明选中的短木棍不合适,需要继续循环遍历下一个短木棍。没有必要验证了,因为肯定会返回false的。(3)如果小于l,说明还没有粘完,还需要继续粘,也要继续循环遍历下一个短木棍。判断接下来能不能递归成功,如果不成功的话,并且cur为0,返回false。为什么只有在cur为0的时候才返回?因为如果当前长度不为0,并且拼接接下来的短木棍仍然不成功,说明此时选择的短木棍不对,需要继续for循环选择下一个合适的短木棍;如果当前长度为0,但不成功,说明在以后的递归中也不可能成功了,就直接false。
代码
#include <iostream>
#include <vector>
#include <algorithm>
#include <cstring>
using namespace std;int n; //短木棍的个数
int l; //长木棍的长度
int num; //长木棍的个数
vector<int> v(65);
bool b[65] = {false}; bool dfs(int s, int j, int cur){ //遍历小木棍的起始位置,拼成的长木棍数目,长木棍当前长度 if (j == num){return true;}for (int i = s; i < n; i++){if (b[i] == true || (i != 0 && v[i] == v[i - 1] && b[i - 1] == false)){continue;} //如果这根木棍已被访问过 或 和上一根没有被访问过的木棍长度相同,剪枝。if (cur + v[i] == l){b[i] = true;if (dfs(0, j + 1, 0)){return true;} //如果继续深度递归能成功,直接返回。 b[i] = false;return false; //如果不能成功,提前终止。 }if (cur + v[i] < l){b[i] = true;if (dfs(i + 1, j, cur + v[i])){ //i + 1,不是s + 1! return true;} //如果继续深度递归能成功,直接返回。 b[i] = false; if (cur == 0){return false;} //不能成功,如果当前长度为0,说明还没有开始拼接 或 已经拼接成了几根,上面的if已经尝试过所有的v[i]了,所以不可能成功。如果当前长度不为0,还可以尝试接下来的v[i]。 } //如果cur + v[i] > l,那么就需要换下一个v[i]来尝试。 }return false; //不是void类型的,不能省略return语句。
}int main(){while (cin >> n && n != 0){int sum = 0;for (int i = 0; i < n; i++){cin >> v[i];sum += v[i];}sort(v.begin(), v.begin() + n, greater<int>()); //从大到小深度搜索,比较好找。for (int i = v[0]; i <= sum; i++){if (sum % i == 0){memset(b, 0, sizeof(b)); //问题出在这里!需要将b数组重置为false,因为有多组测试用例! l = i;num = sum / l;if (dfs(0, 0, 0)){cout << l << endl;break;}} }}return 0;
}