粒子群算法(Particle Swarm Optimization,PSO)是一种基于群体智能的优化算法,其思想来源于鸟群寻食和鱼群捕食等自然现象。PSO算法通过模拟群体智能的行为,以一种启发式的方式寻找最优解,因此具有全局搜索能力强、收敛速度快等优点。本文将介绍标准粒子群算法的基本流程、算法实现和应用场景等方面。
完整代码下载方式
(1)改进粒子群优化算法||粒子群算法变体||Improved particle swarm optimization algorithm
一、算法实现
1.1 标准的粒子群算法
文献[1]在更新粒子的速度和位置时,需要考虑每个粒子自身的经验和整个群体的经验。具体的更新公式如下:
v i , j = w v i , j + c 1 r 1 ( p b e s t i , j − x i , j ) + c 2 r 2 ( g b e s t j − x i , j ) (1) v_{i,j}=wv_{i,j}+c_1r_1(pbest_{i,j}-x_{i,j})+c_2r_2(gbest_{j}-x_{i,j}) \tag{1} vi,j=wvi,j+c1r1(pbesti,j−xi,j)+c2r2(gbestj−xi,j)(1)
x i , j = x i , j + v i , j (2) x_{i,j}=x_{i,j}+v_{i,j} \tag{2} xi,j=xi,j+vi,j(2)
其中, v i , j v_{i,j} vi,j表示粒子 i i i在第 j j j维的速度, x i , j x_{i,j} xi,j表示粒子 i i i在第 j j j维的位置, p b e s t i , j pbest_{i,j} pbesti,j表示粒子 i i i在第 j j j维的个体最优解, g b e s t j gbest_{j} gbestj表示整个群体在第 j j j维的全局最优解, w w w表示惯性权重, c 1 c_1 c1和 c 2 c_2 c2分别表示个体学习因子和社会学习因子, r 1 r_1 r1和 r 2 r_2 r2分别表示0到1之间的随机数。
1.2、粒子速度更新公式的改进
粒子速度更新公式的改进
文献【2】提出一种均值粒子群优化(MeanPSO)算法,即利用个体最优和群体最优的线性组合 ( p h e s t i j + g b e s t j 2 ) ({\frac{{\mathrm{phest}}_{i j}+{\mathrm{gbest}}_{j}}{2}}) (2phestij+gbestj)和 ( p h e s t i j − g b e s t j 2 ) ({\frac{{\mathrm{phest}}_{i j}-{\mathrm{gbest}}_{j}}{2}}) (2phestij−gbestj)分别替换
MeanPSO算法中粒子搜索区间更广,使得算法在进化前期有更大可能搜索到全局最优解。
具体对(1)式的更新公式如下:
v i j ( t + 1 ) = w v i j ( t ) + c 1 r 1 ( p h e s t i j − g b e s t j 2 − x i j ( t ) ) + c 2 r 2 ( p b e s t i − g b e s t d 2 − x i j ( t ) ) (3) v_{ij}(t+1)=w v_{i j}(t)+c_{1}r_{1}\left({\frac{{\mathrm{phest}}_{i j}-{\mathrm{gbest}}_{j}}{2}}\,-x_{i j}(t)\right)+c_{2}r_{2}\left({\frac{{\mathrm{pbest}}_{i }-{\mathrm{gbest}}_{d}}{2}}\,-x_{i j}(t)\right) \tag{3} vij(t+1)=wvij(t)+c1r1(2phestij−gbestj−xij(t))+c2r2(2pbesti−gbestd−xij(t))(3)
MeanPSO算法中粒子搜索区间更广,使得算法在进化前期有更大可能搜索到全局最优解.
二、仿真实验及结果分析
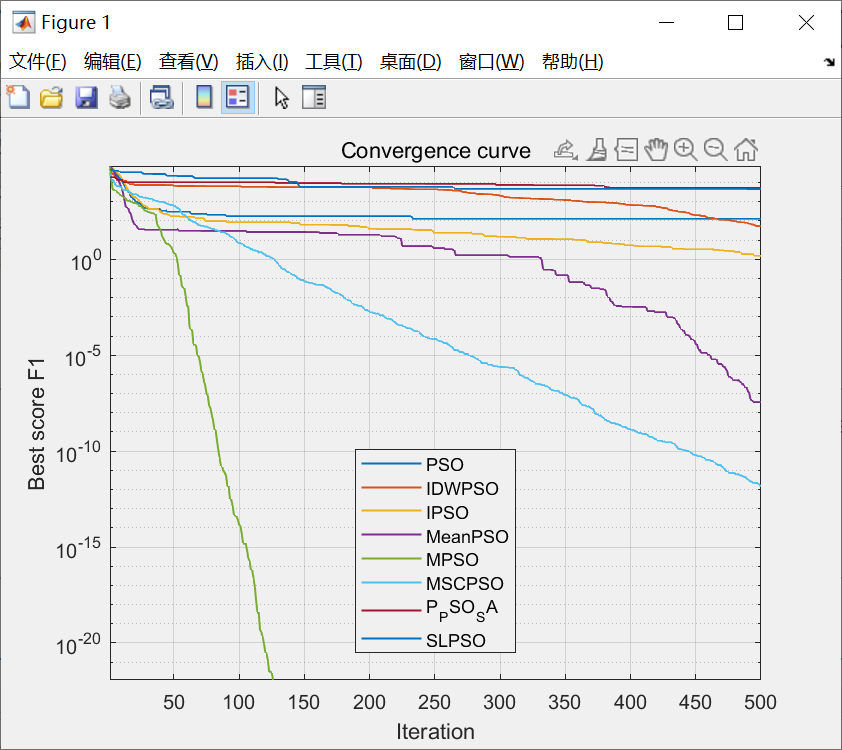
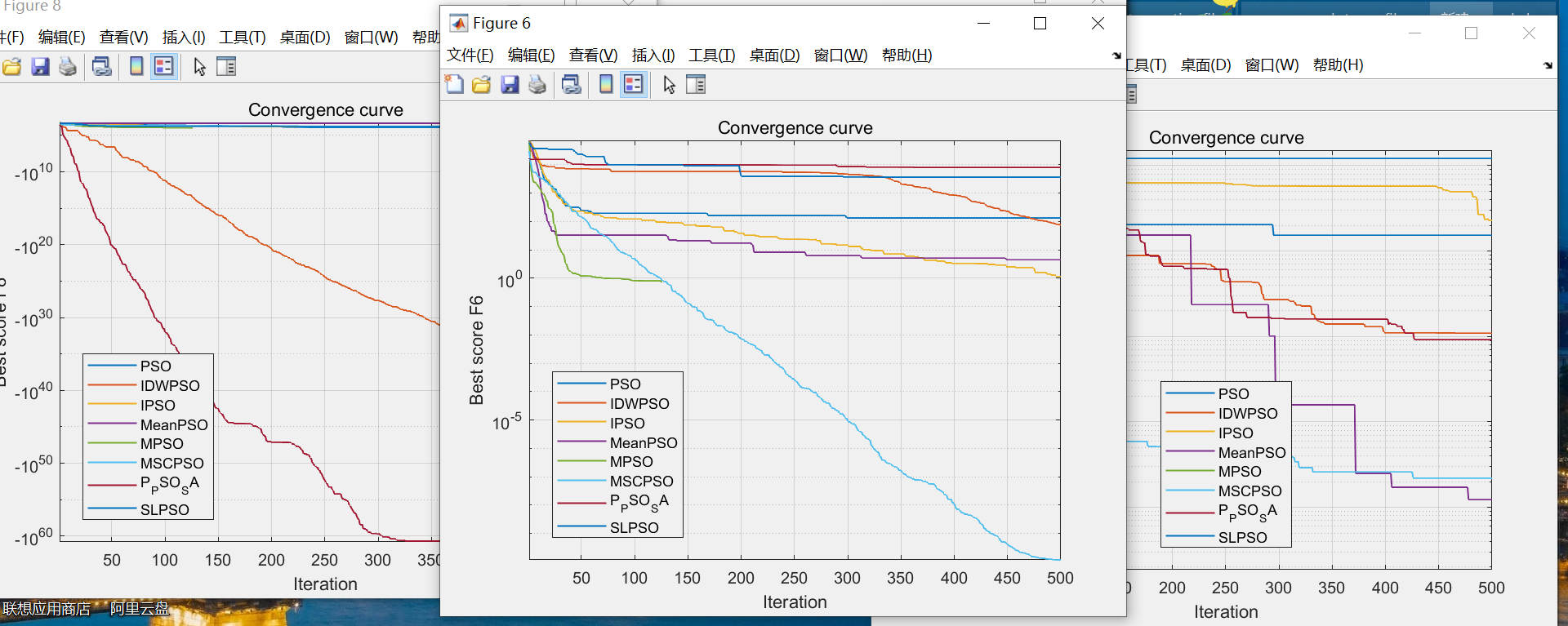
为验证文献[3]所提算法MPSO有效性,将文献[3]MPSO算法与粒子群优化(PSO)算法【1】、均值粒子群优化(MeanPSO)算法【2】、一种基于自适应策略的改进粒子群优化(MPSO)算法【3】、改进粒子群算法(IPSO)【4】,一种多群自适应协同粒子群优化算法(MSCPSO)算法[5]、社会学习粒子群优化(SL-PSO)算法【6】、一种动态调整惯性权重的混合粒子群算法【7】,一种结合自适应惯性权重的混合粒子群算法【8】进行对比测试,使用Matlab软件进行仿真,不同PSO算法设置相同种群规模N = 30、最大迭代次数 T max = 500 T_{\max}=500 Tmax=500和变量维数D=30。
三、完整代码下载方式
(1)改进粒子群优化算法||粒子群算法变体||Improved particle swarm optimization algorithm
三、完整代码下载方式
(1)改进粒子群优化算法||粒子群算法变体||Improved particle swarm optimization algorithm
【1】KENNEDY J,EBERHART R C.Particle swarm optimizationC//Proceedings of the lEEE International Conference on Neural Networks,1995:1942-1948
【2】 Deep K, Bansal J C. Mean particle swarm optimisation for function optimisation[J]. International Journal of Computational Intelligence Studies, 2009, 1(1): 72-92.
【3】Hao Liu, Xu-Wei Zhang , Liang-Ping Tu. A modified particle swarm optimization using adaptive strategy[J]. Expert Systems With Applications, 2020, 152: 113353.
【4】Y. Shi, R. Eberhart. A modified particle swarm optimizer[C]. 1998 IEEE International Conference on Evolutionary Computation Proceedings. IEEE World Congress on Computational Intelligence (Cat. No.98TH8360), 1998, 4: 69-73.
【5】Jiuzhong Zhang, Xueming Ding.A Multi-Swarm Self-Adaptive and Cooperative Particle Swarm Optimization[J].Engineering Applications of Artificial Intelligence,2021,24(6),958-967.
【6】Ran Cheng, Yaochu Jin. A social learning particle swarm optimization algorithm for scalable optimization[J].Information Sciences, 291,43-60.
【7】胡堂清,张旭秀,曹晓月.一种动态调整惯性权重的混合粒子群算法[J].电光与控制,2020,27(06):16-21.
【8】于桂芹,李刘东,袁永峰.一种结合自适应惯性权重的混合粒子群算法[J].哈尔滨理工大学学报,2016,21(03):49-53.