1.时间复杂度

2.树,森林,二叉树的转换
2.1树转二叉树
- 给所有的兄弟节点之间加一条连线;
- 去线,只保留当前根节点与第一个叶子节点的连线,删除它与其他节点之间的连线;
- 然后根据左孩子右兄弟进行调整;
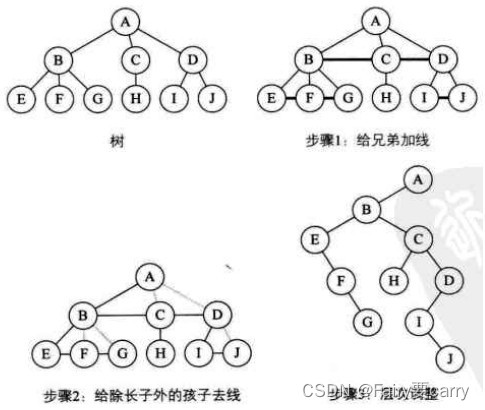
2.2森林转为二叉树
把森林的每棵树转为二叉树(遵循左孩子右兄弟即可)
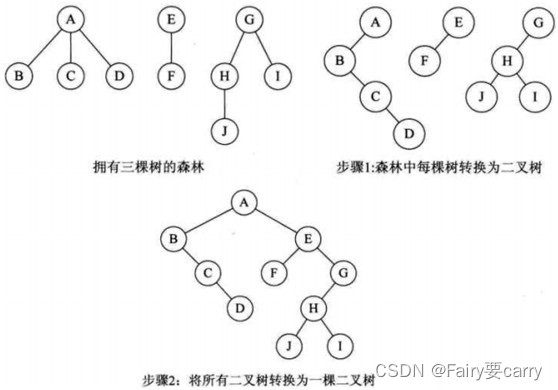
2.3二叉树转为森林
当一颗二叉树的根节点有右孩子,则说明这颗二叉树能够转换为森林;
- 从根节点开始,若存在右孩子,则把与右孩子节点的连线删除。再查看分离后的二叉树,若其根节点的右孩子存在,则连线删除…。直到所有这些根节点与右孩子的连线都删除为止。
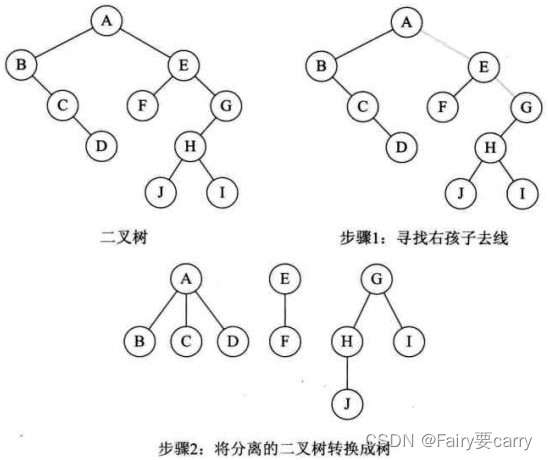

二叉树的N1再减去一个1就为T1;
3.链表的操作
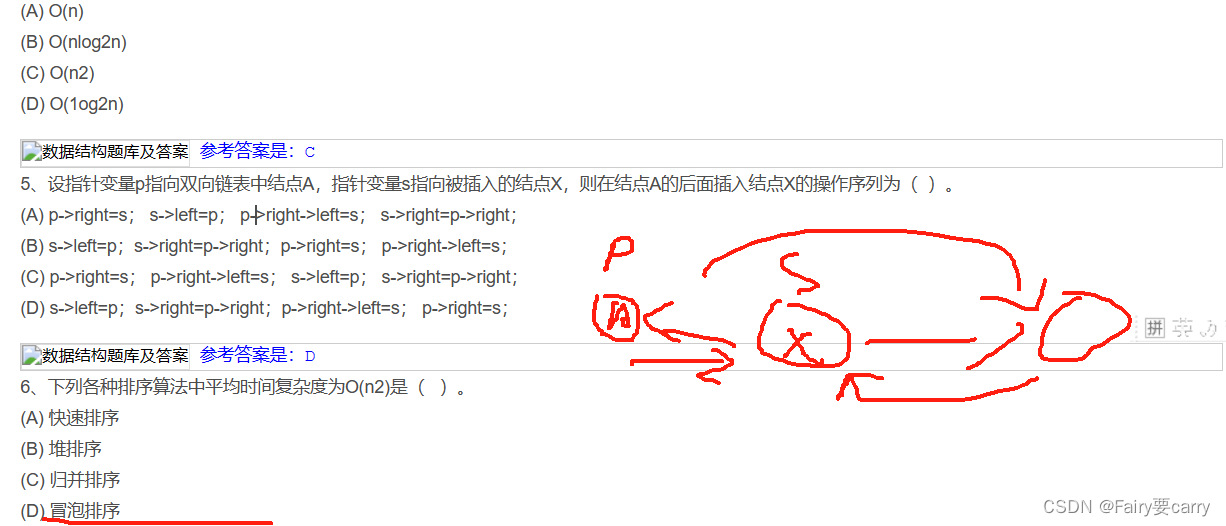
4.树的操作

从子节点的角度,共有节点数为:度数为3的子节点数+度数为2的子节点数+度数为1的子节点数+根节点数=32+21+1*2+1=11;
从父节点的角度,共有节点数为:度数为3的节点数+度数为2的节点数+度数为1的节点数+度数为0的节点数=2+1+2+x;
解得x=6
5.平均比较次数的计算
平均比较次数=总比较次数/元素待查找的概率;
6.平均查找长度:

根据分块查找的原理,平均查找长度可以通过每块的平均查找长度乘以每块的概率来计算。在这个问题中,每块的平均查找长度为3(由于每块有6个元素,所以平均查找长度为6/2=3),每块的概率为1/5。
因此,平均查找长度为:
(1 * 1/5) + (2 * 1/5) + (3 * 1/5) + (4 * 1/5) + (5 * 1/5) = 15/5 = 3
接着,在块内查找元素的平均查找长度为:
(1 * 1/6) + (2 * 1/6) + (3 * 1/6) + (4 * 1/6) + (5 * 1/6) + (6 * 1/6) = 21/6 = 3.5
最后,将两个结果相加得到平均查找长度:
3 + 3.5 = 6.5
所以,平均查找长度为6.5;
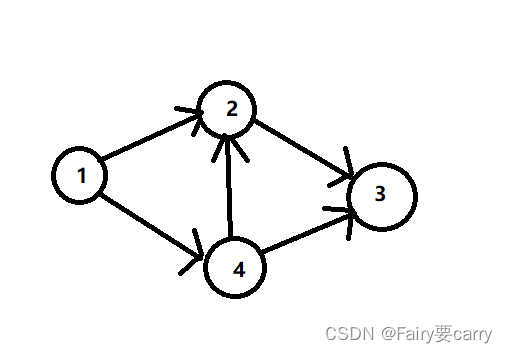
7.拓扑序列:
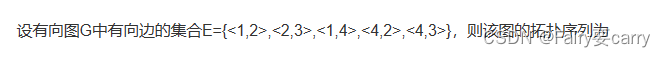
首先按照集合关系画出有向图,从图中选出入度为0的①的顶点并输出,删除从①顶点发出来的所有有向边。然后再选择一个入度为0的顶点④并输出,删除从④顶点发出来的所有有向边,按此规律反复,最后得到的拓扑排序为(1,4,2,3)
8.循环队列和栈

最多能够存储m-1个元素;
栈的长度为m,表示可以存储m个元素,因为栈是一种后进先出(LIFO)的数据结构,插入和删除操作都在栈顶进行,所以不需要额外的空间来区分栈空和栈满的状态。
9.冒泡排序:

8,8
10.排序算法空间复杂度和时间复杂度:

1.在堆排序和快速排序中,如果从平均情况下排序的速度最快的角度来考虑,应该选择快速排序。因为在平均情况下,快速排序的时间复杂度为O(n log n),比堆排序略快。
2.而如果从节省存储空间的角度来考虑,则最好选择堆排序。因为堆排序是一种原地排序算法,不需要额外的存储空间,而快速排序在递归的过程中需要消耗大量的栈空间,所以在存储空间方面,堆排序更有优势。
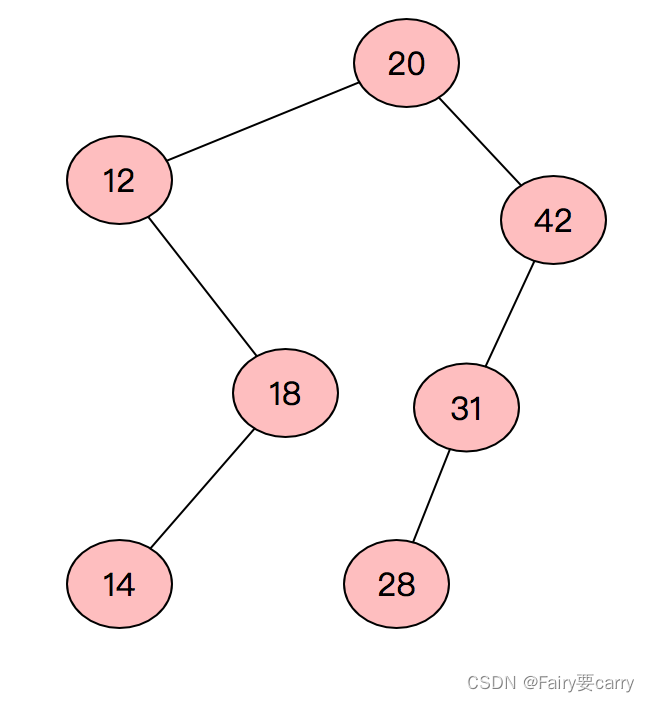
11.平均查找长度:

1.先画出排序二叉树——>2.(1+22+32+42)/7=19/7;(比较次数=层数——>比较次数当前层数的节点数)
12.哈夫曼树
哈夫曼树就是:两个最小的节点构造一个较大的节点;

13.初始化堆

(24,65,33,80,70,56,48)——>小根堆思想
(80,70,56,65,24,33,48) ——>大根堆
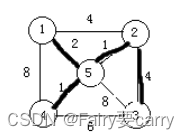
14.最小生成树上所有边的权值和:

方法: 一种是随意从一个点开始,找权值最小的路径,另一种就是依次找最短的边的,舍去形成回路的边,直到遍历所有结点
15.有向图中的邻接表和邻接矩阵

**邻接表:**是一种顺序分配和链式分配相结合的存储结构。
**逆邻接表:**任一表头结点下的边结点的数量是图中该结点入度的弧的数量,与邻接表相反。
逆邻接表中边节点个数等于邻接表边结点个数。表结点个数相同,但是头结点个数不一定相同。
16.链表的知识点
链表插入和删除只是改变了相应节点的指针指向,地址并没有改变,所以不必移动
17.邻接矩阵知识点:

邻接表:0(v+e);
邻接矩阵:0(v^2);

邻接矩阵存储时,无论有向图还是无向图,也无论边的数目是多少,其存储空间都是O(n的平方),书上原话,所以邻接矩阵存储空间与边的数目无关