参考资料:python统计分析【托马斯】
正态分布或高斯分布是所有分布函数中最重要的。这是由于当样本数足够大的时候,所有分布函数的平均值都趋近于正态分布。数学上正态分布的特征有平均数μ和标准差σ确定。
其中,-∞<x<∞,f_μ,σ是正态分布的概率密度函数(PDF)。和离散型分布的概率质量函数(PMF)相比,PMF只针对离散的整数定义,而PDF针对的是连续的数值。标准正态分布分布是均值为0,标准差为1的正态分布,并且有时被称为z分布。

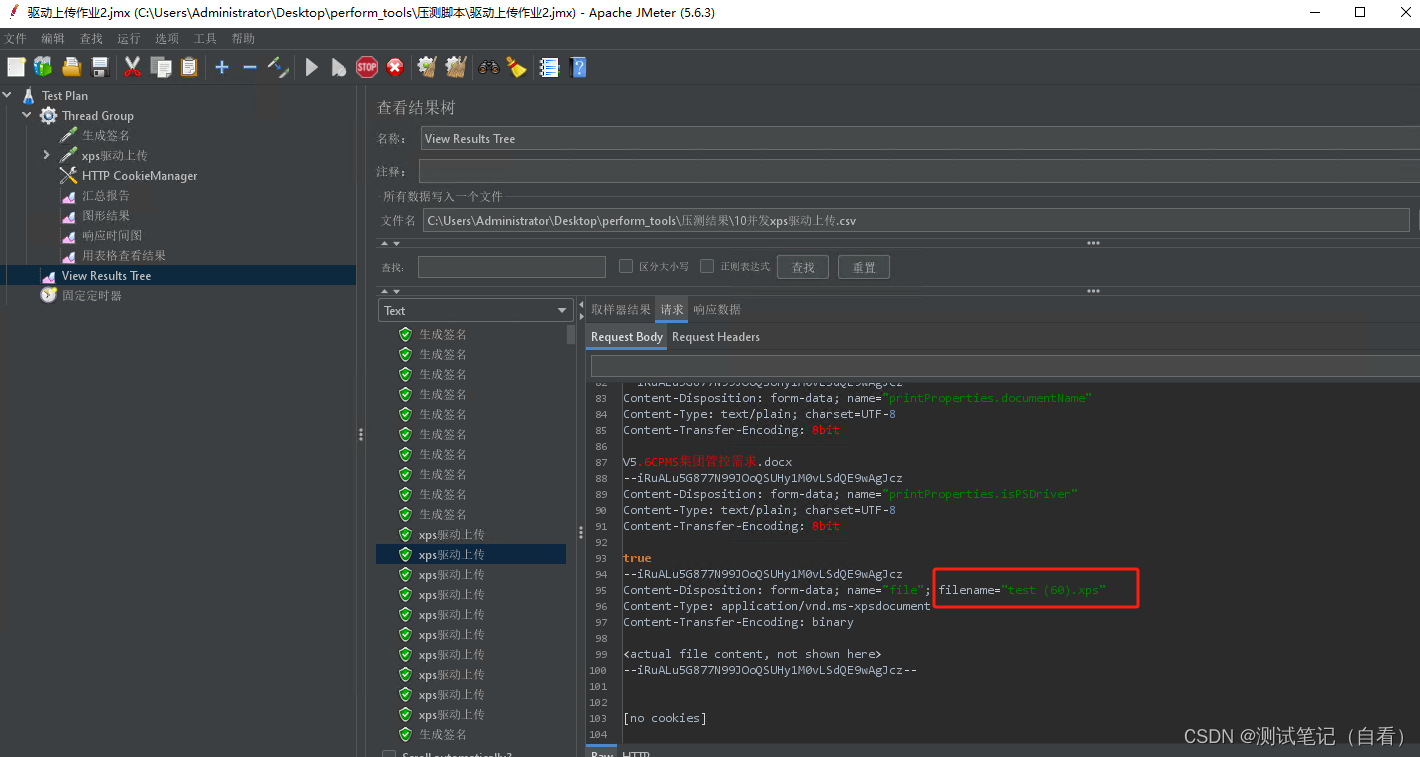
代码操作如下:
# 导入库
import numpy as np
from scipy import stats
# 定义正态分布参数
mu=-2
sigma=0.7
# 设置正态分布
myDistribution=stats.norm(mu,sigma)
# 定义显著性水平
alpha=0.05
# 计算包含95%数据的区间
myDistribution.ppf([alpha/2,1-alpha/2])
1、正态分布的例子
①如果男性平均身高是175cm,标准差是6cm,那么一个随机选择的男性身高是183的概率是多少?
②如果假定罐头的标准差为4g,那么平均重量需要是多少,才可以确保99%罐头的重量至少为250g?
③如果男性平均身高175cm、标准偏差为6cm,女性平均身高为168cm、标准偏差为3cm,那么随机选择的男性比随机选择的女性要矮的概率是多少?
2、中心极限定理
中心极限定理说的是,一个足够大数量的同分布的随机变量的均值,将近似服从正态分布分布。换句话说,无论分布如何,均值的抽样分布趋于正态。如下图所示,对超过10个均匀分布的数据进行平均化,已经能够产生平滑的近似高斯分布。

3、分布和假设检验
为了说明分布函数和假设检验之间的关系,让我们一步一步分析下面的问题。
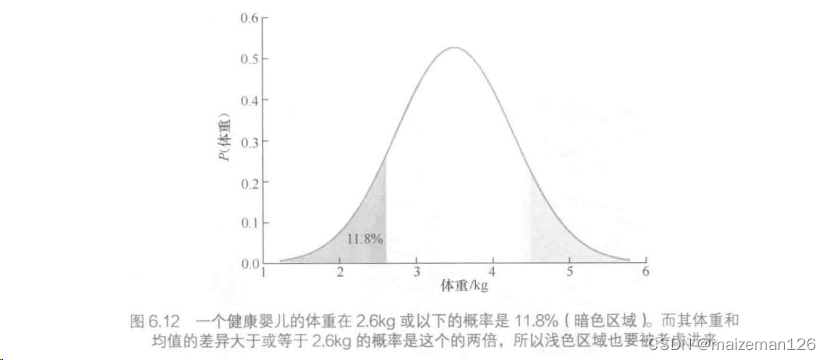
假设新生儿的平均体重为3.5kg,标准偏差为0.76kg。如果我们想检查出来所有与普通婴儿显著不同的孩子,我们应该如何判断一个出生体重为2.6kg的孩子?
我们可以用假设检验的形式重新阐述这个问题:我们的假设是,该婴儿来自健康婴儿总体。根据这个婴儿的体重,我们可以保留这个假设,或者我们应该拒绝这个假设。
为了回答这个问题我们可以按照如下步骤:
①找到描述健康婴儿特征的分布:μ=3.5,σ=0.76。
②计算在我们感兴趣的值处的CDF。CDF(2.6)=0.118,即一个健康婴儿的体重比平均体重轻至少0.9kg的概率是11.8%。
nd=stats.norm(3.5,0.76)
nd.cdf(2.6)
③由于这是正态分布,健康婴儿比平均婴儿体重重至少0.9的概率也是11.8。
④解释结果:如果该婴儿是健康的,那么它的体重偏离均值至少0.9kg的概率是2*11.8%=23.6%。这并不显著,所以我们没有足够的证据拒绝我们的假设,所以我们认为该婴儿是健康的。