题目链接

AcWing 180. 排书

题目描述

给定$n$ 本书，编号为 $1\sim n$。

在初始状态下，书是任意排列的。

在每一次操作中，可以抽取其中连续的一段，再把这段插入到其他某个位置。

我们的目标状态是把书按照$1\sim n$ 的顺序依次排列。

求最少需要多少次操作。

输入格式

第一行包含整数$T$，表示共有$T$组测试数据。
每组数据包含两行，第一行为整数$n$，表示书的数量。
第二行为$n$个整数，表示$1\sim n$ 的一种任意排列。

同行数之间用空格隔开。

输出格式

每组数据输出一个最少操作次数。

如果最少操作次数大于或等于$5$次，则输出5 or more。

每个结果占一行。

数据范围

$1\le n\le 15$

输入样例

3
6
1 3 4 6 2 5
5
5 4 3 2 1
10
6 8 5 3 4 7 2 9 1 10

输出样例

2
3
5 or more

算法思想

根据题目描述，需要对$1\sim n$的一个排列，进行若干次操作，在每一次操作中，可以抽取序列中连续的一段，再把这段插入到其他某个位置。问最少经过几次操作，可以将序列变为按照$1\sim n$ 的顺序依次排列。

先考虑每一次操作的决策数量：

• 当从序列中抽取长度为$i$的一段时，有$n-i+1$种选择。例如：对于长度$n=6$的序列中，抽取长度为$i=3$的连续一段，有$4$种选择，如下图所示
  
• 对于每种抽法，有$n-i$种放法，即将长度为$i$的一段插入其它$n-i$个空中。例如：
  

那么每一步状态数量为$(n-i)\times (n-i+1)$，但将某一段向前移动，等价于将跳过的那段向后移动，因此每种移动方式被计算了两次，还要除以$2$。所以状态空间的大小为${\sum }_{i=1}^n(n-i)\times (n-i+1)/2\le (15\times 14+14\times 13+...+2\times 1)/2=560$。

考虑在$4$步内找到答案，最多有$560^4$个状态，暴力搜索会超时。可以使用双向广搜 或者迭代加深A*（IDA* ）来优化。

迭代加深A*

在A*算法算法中，将估价函数与优先队列BFS结合，提高了搜索效率。那么把估价函数与迭代加深的DFS结合就是迭代加深$\text{A*}$（$\text{IDA*}$）。

迭代加深$\text{A*}$要限定一个深度，在不超过该深度的前提下执行DFS，若找不到解，就扩大深度限制，重新进行搜索；除此之外，还要设计一个估价函数，估算从每个状态到目标状态需要的“步数”。与$\text{A*}$算法一样，估价函数需要遵守“预计值不大于未来实际步数”的准则。

基本思想是以迭代加深DFS的搜索框架为基础，把原来简单的深度限制加强为：若当前深度+未来估计步数>深度限制，则立即从当前分支回溯。

估价函数

$\text{IDA*}$的算法的关键在于设计估价函数，那么本题的估价函数如何设计？考虑对于目标状态，第$i$本书后边应该是第$i+1$本书，那么认为$i+1$是$i$的正确后继。

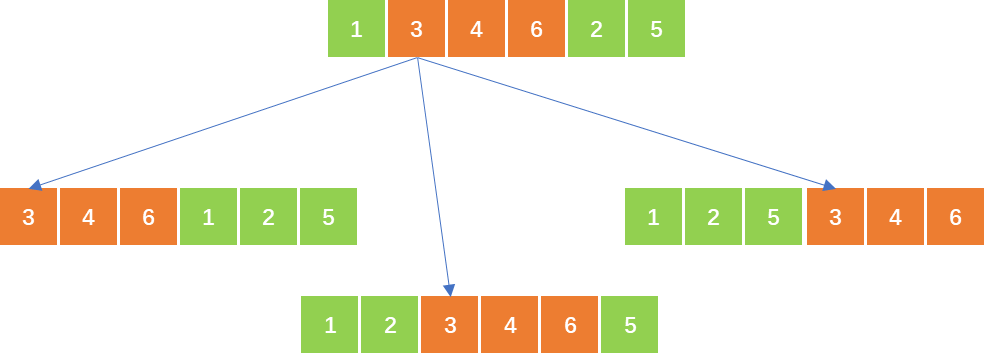
对于任意状态，考虑整个排列中错误的后继总数，将其记为tot，可以发现每次操作至多更改$3$本数的后继，例如，将$346$移动到$2$的后面，$1、2、6$的后继被更改，如下图所示：
也就是说，在最理想的情况下，每次操作都能把$3$个错误后继全部该对，那么消除所有错误后继的操作次数也至少需要$\lceil \frac{tot}{3}\rceil$次。

因此，可以把一个状态state的估价函数设计为$h(state)=\lceil \frac{tot}{3}\rceil$，其中tot表示在当前状态state下书的错误后继总数。

算法实现

基本思想是使用迭代加深的方法，从$1\sim 4$依次限制搜索深度，然后从起始状态出发进行DFS。对于当前状态：

• 如果若当前步数+未来估计步数>深度限制，则搜索结束返回无解。
• 如果到达最终状态，搜索结束返回有解。
• 枚举要抽连续的一段的左右位置$[L,R]$，以及插入位置$i$，将$[L,R]$这一段插入到$i$位置后
  • 继续搜索下一阶段的状态

代码实现

#include <bits/stdc++.h>
using namespace std;
const int N = 20;
int n, q[N], b[5][N]; //备份数组
int h() //估价函数
{int tot = 0; //统计错误后继总数for(int i = 0; i + 1 < n; i ++)if(q[i] + 1 != q[i + 1]) tot ++;return (tot + 2) / 3; //总数÷3向上取整
}
bool check()
{for(int i = 0; i < n; i ++)if(q[i] != i + 1) return false;return true;
}
//当前步数k，限制深度depth
bool dfs(int k, int depth)
{if(k + h() > depth) return false; //当前步数+估计步数超过限制if(check()) return true;//枚举抽取的左右两端和插入位置for(int L = 0; L < n; L ++)for(int R = L; R < n; R ++)for(int i = R + 1; i < n; i ++) //注意只需要枚举后面的插入位置即可{memcpy(b[k], q, sizeof q); //备份，方便恢复现场int x, y;//将[R+1,i]位置上的数向前移动for(x = R + 1, y = L; x <= i; x ++, y ++) q[y] = b[k][x];//将[L,R]位置上的数，向后移动for(x = L; x <= R; x ++, y ++) q[y] = b[k][x];if(dfs(k + 1, depth)) return true;memcpy(q, b[k], sizeof q); //备份，方便恢复现场}return false;
}
int main()
{int T;cin >> T;while(T --){cin >> n;for(int i = 0; i < n; i ++) cin >> q[i];int depth = 0;while(depth < 5 && !dfs(0, depth)) depth ++;if(depth >= 5) puts("5 or more");else cout << depth << '\n';}return 0;
}