第十二届蓝桥杯省赛CC++ 研究生组

十二届省赛题

第十二届蓝桥杯省赛C&C++ 研究生组-卡片
第十二届蓝桥杯省赛C&C++ 研究生组-直线
第十二届蓝桥杯省赛C&C++ 研究生组-货物摆放
第十二届蓝桥杯省赛C&C++ 研究生组-路径
第十二届蓝桥杯省赛C&C++ 研究生组-时间显示
第十二届蓝桥杯省赛C&C++ 研究生组-砝码称重
第十二届蓝桥杯省赛C&C++ 研究生组-异或数列
第十二届蓝桥杯省赛C&C++ 研究生组-双向排序

三年小小结

水过了最新三年的题目，小小复盘一下~

简单模拟

卡片（填空）：从1开始计算每位所用卡片，当某个数字的卡片不足时，则找到能拼到的最大数。注意最后的这个数是拼不出来的第一个数，所以答案记得减一。作为填空题，枚举即可解决，该题目进一步思考的话，一定是卡片1消耗量最大，可转化为1出现2021次的数字
直线（填空）：判断给定范围内的点能组成多少条不同直线，表面考算法，其实是考数学公式~注意分母不为0，直接把平行于y轴的单算即可，记得后续加上。
时间显示：常见的时间处理类问题，小小注意下小时是24小时制。需要显示的时间是时（0-23）分（0-59）秒（0-59），给的输入是从00-00-00开始的毫秒数，则该先除的先除该求余的求余。给的年份就是迷惑性信息了，木用，忽略即可。
裁纸刀（填空）：先裁四下去掉边缘，再把行分开（行数-1），再把列分开（（列数-1）*行数）。甚至都没啥小坑，温柔
灭鼠先锋（填空）：手动可以直接模拟~ 再优化一点点的话，对于一行空内容的话，谁先手谁必输，问题等价于谁后把第一行填满，谁就一定能保证自己赢。问题分解的思想很有效，简单分割也许就能大幅简化问题
与或异或（填空）：电路图看起来挺唬人的，但枚举就能解决的纸🐅。本质上就是按照a[i][j] = a[i-1][j] op a[i-1][j+1]，其中op可选&、^、|其一，统计结果为1的组合个数。
翻转：翻转规则为出现010或101就可以把中间的值翻转，借助翻转的情况下是否能把两个串变相同，如果是输出最小翻转次数。虽然题设中有“翻转操作可无限重复”，但其实一次翻转即可，翻完了其实也就不能出现不同了，属于干扰信息。以s串1010101为例，翻转第一次1000101，翻转第二次1000111，搞定。

excel

工作时长（填空）：本质上要求的是两个时间段之差的和。用excel先排序；再选择时间格式[h]:mm:ss，注意小时的选择，以处理超出24小时的情况；计算两个时间段的差，关于求出整列的上下行间的时间差，先手算两个单元格，后续直接下拉即可自动计算；求和

数学问题

质因数

很稳定，每年都考了一个，或直接或加了点马甲

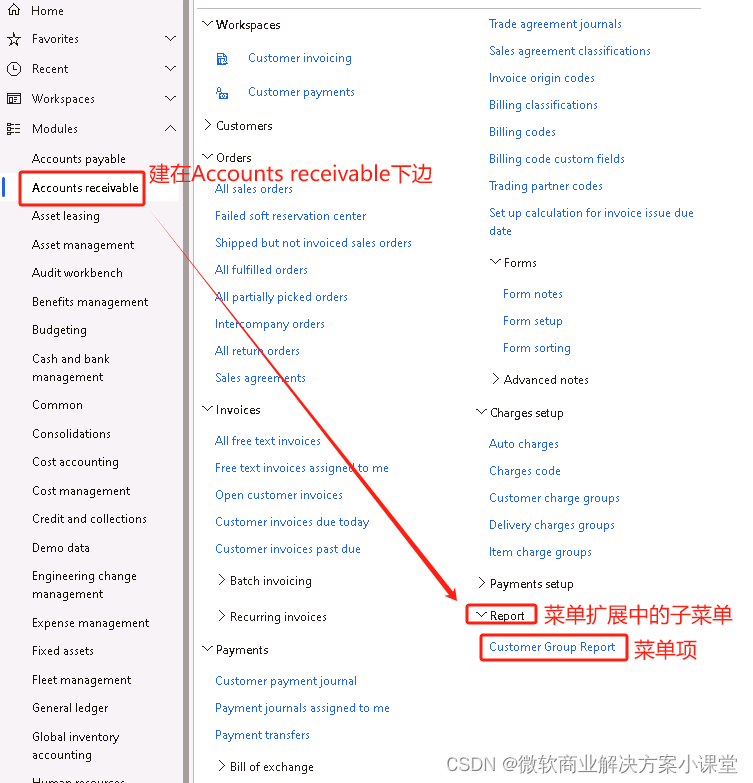
货物摆放（填空）：整数分解问题。n较大直接暴力枚举不可行，考虑当时质因数模块学过整数范围内一定能用十个质因数表示，类推n的约数也不会太多，转化为先求出n的约数（别漏了1和n），再计算相乘为n的组合个数
质因数个数：给出整数n的质因数个数

sqr = sqrt(1.0*n);
num = 0;
for(int i = 2; i <= sqr; i++){if(n % i == 0){num++;while(n % i == 0) n /= i;}
}
if(n > 1) num++;//别漏了最后这个顽固分子~

公因数匹配：找到首次出现或同时出现但最短的区间，满足头尾元素有大于1的公因数。直接暴力的话两层的10⁵超时，有了之前的经验，也考虑下先分解看看。分解每个数的所有质因数，如果没出现过，则记录首次出现的位置；如果已经出现过，判断是否需要更新最左位置。判断该数满足的区间是否早于或短于已有的区间，若是则更新。

#include<stdio.h>
#include<math.h>
const int maxn = 1e6 + 10;
int p[maxn] = {0};
int main(){int n, x, l, ansL, ansR = 0, sqr;scanf("%d", &n);ansL = n + 1;for(int i = 1; i <= n; i++){l = n + 1;scanf("%d", &x);sqr = sqrt(1.0 * x);for(int j = 2; j <= sqr; j++){if(x % j == 0){if(!p[j]) p[j] = i;else if(p[j] < l) l = p[j];while(x % j == 0) x /= j;}}if(x > 1){if(!p[x]) p[x] = i;else if(p[x] < l) l = p[x];}if(l < ansL || (ansL == l && ansR > i)){ansL = l;ansR = i;}}printf("%d %d", ansL, ansR);return 0;
}

说都说了，顺带复习下最小公约数&最大公倍数

int gcd(int a, int b){//辗转相除法求最大公约数，时间复杂度O(logn) if(!b) return a;return gcd(b, a % b);
}最小公倍数为a * b / gcd(a, b)

数的拆分：给出整数n，将其拆分为x²* y³(大于2和偶数次幂可以转化为底数先升幂再把幂次调到2，奇数次幂同理,例如x⁴=x²的平方，y⁵=y²的平方 *y)的形式则可拆分返回yes，否则返回no。n最大为10e18,开五次方大约是4000，则我们对4000以内的质数打表，分解后的约数就不会太大了。判断是否能够融入我们要求的模式，即能否转化为平方或立方，能则该数可以拆分，否则是个单蹦不能拆分。

进制转换

异或数列：十进制转二进制。各方初始值为0，给定数列，选数异或，每个数只能选用一次。显然，谁先抢到最高位的“唯一”（1个或奇数的单蹦1）一个1则必胜。问题转化为寻找：
- 最高位的唯一的一个1
- 最高位的偶数个1
  - 总的零的数量为偶数个，先手拿到单蹦1则必胜
  - 总的零的数量为奇数个，后手拿到单蹦1则必胜

否则为平局
2.

阶乘特点

阶乘的和：直接算的话肯定超时，而且仔细想来只是求最大的m，并不需要真的算出和，只是能进行比较即可，算出来也是多余工作。回到问题本身阶乘m!，我们有多个a_i!，对于多个阶乘有(m+1)m! = (m+1)!，我们对a_i进行排序，顺带统计每个数的出现次数，要有序且有映射关系考虑用map；自底到高统计每位是否能进位，第一个不能进位前的数就是我们要找的m

求余

GCD：考查辗转相除法和求余的简化。思维更简单的解法，观察知最大公约数是abs(a-b)，从1开始依次枚举即可，能骗些分数。进一步思考的话，回到问题本身，
- 找使得gcd(a+k,b+k)最大的k，根据辗转相除算法知，gcd(a+k,b+k)=gcd(b+k,b-a)
- gcd(b+k,b-a) = b-a（假设已经处理好，能保证b >= a）
- 转化为找到满足(b+k)%(b-a) == 0的最小值
- 记g = b- a，则(b+k)%g = (b % g + k % g) % g == 0
  b % g <g, k % g < g,则g - b % g = k

#include<iostream>
#include<algorithm>
using namespace std;
int main(){long long a, b, g;scanf("%lld%lld", &a, &b);if(a > b) swap(a, b);g = b - a;printf("%lld", g - b % g);return 0;
}

观察规律

全排列的价值：观察给出的样例知，对于1~n, 前后两两价值相加的和都相等，为(n-1)*n/2;那再看可以组数，也就是排列数n!/2（除2是因为两两一组相加才为定值）

动态规划

砝码称重：很经典的一个问题。我们能称出来的最大重量是所有砝码重量之和，最小的可能重量是1，其中题设告诉我们砝码总重范围也是一种暗示了。
利用dp的话，我们依次计算有1~n个砝码能称出来的重量，首先前i个砝码能称出来的重量，也一定能用前i+1个砝码称出来。对于前i个砝码的判断，之前称不出来的重量m，考虑
- 第i个砝码重量w[i] == m
- 已经可以称出来m + w[i]
- 已经可以称出来abs(m - w[i])
  - m > w[i],能称出来m-w[i]，则再加个w[i]
  - w[i] < m,能称出来w[i]-m，则在对面来个w[i]

最后统计用n个砝码所能称出的重量个数即可

int dp[N][maxn] = {0};
count = 0;
for(int i = 1; i <= n; i++){for(int j = 1; j <= sum; j++){dp[i - 1][j] = 1;if(!dp[i][j]){if(w[i] == j || a[i - 1][j + w[i]] || a[i - 1][abs(j - w[i])]) dp[i][j] = 1;}}
}for(int i = 1; i <= sum; i++)count += dp[n][i];