目录
前言
面试题 88 : 爬楼梯的最少成本
一、分析确定状态转移方程
二、递归代码
三、使用缓存的递归代码
四、空间复杂度为 O(n) 的迭代代码
五、空间复杂度为 O(1) 的迭代代码
前言
动态规划是目前算法面试中的热门话题,应聘者经常在各大公司的面试中遇到需要运用动态规划才能解决的问题。由于动态规划相关的面试题题型变化多样,有时让人琢磨不透,因此很多应聘者认为动态规划是算法面试中的一个难点。
其实,在深入理解动态规划之后就能发现其实运用动态规划解决算法面试题是有套路的。运用动态规划解决问题的第 1 步是识别哪些问题适合运用动态规划。和适用运用回溯法的问题类似,适用动态规划的问题都存在若干步骤,并且每个步骤都面临若干选择。如果题目要求列举出所有的解,那么很可能需要用回溯法解决。如果题目是求一个问题的最优解(通常是最大值或最小值),或者求问题的解的数目(或判断问题是否存在解),那么这个题目有可能适合运用动态规划。
例如,给定一个没有重复数字的正整数集合,请列举出所有元素之和等于某个给定值的所有组合。同一个数字可以在组合中出现任意次。例如,输入整数集合 [2, 3, 5],元素之和等于 8 的组合有 3 个,分别是 [2, 2, 2, 2]、[2, 3, 3] 和 [3, 5]。
这个题目要求列举出所有符合条件的组合,即找出问题的所有解,可以用回溯法解决这个问题。
又如,给定一个没有重复数字的正整数集合,请找出所有元素之和等于某个给定值的所有组合的数目。同一个数字可以在组合中出现任意次。例如,输入整数集合 [2, 3, 5],组合 [2, 2, 2, 2]、[2, 3, 3] 和 [3, 5] 的和都是 8,因此输出组合的数目 3。
这个题目看起来和前一个很相像,但它们有一个根本区别:第 1 个题目要求列举出所有的组合,因此很适合采用回溯法;第 2 个题目只需要求出符合条件的组合的数目,对具体的每个组合不感兴趣,因此可以采用动态规划解决这个问题。
在采用动态规划时总是用递归的思路分析问题,即把大问题分解成小问题,再把小问题的解合起来形成大问题的解。找出描述大问题的解和小问题的解之间递归关系的状态转移方程是采用动态规划解决问题的关键所在。下面将按照 "单序列问题"、"双序列问题"、"矩阵路径问题" 和 "背包问题" 等常见题型详细讨论如何采用递归的思路分析问题并最终运用动态规划解决问题。
分治法也是采用递归思路把大问题分解成小问题。例如,快速排序算法就是采用分治法。分治法将大问题分解成小问题之后,小问题之间没有重叠的部分。例如,快速排序算法将一个数组分成两个子数组,然后排列两个子数组,这两个子数组之间没有重叠的部分。如果应用递归思路将大问题分解成小问题之后,小问题之间没有相互重叠的部分,那么可以直接写出递归的代码实现相应的算法。
如果将大问题分解成小问题之后,小问题相互重叠,那么直接用递归的代码实现就会存在大量重复计算。小问题之间存在重叠的部分,这是可以运用动态规划求解问题的另一个显著特点。
在用代码实现动态规划的算法时,如果采用递归的代码按照从上往下的顺序求解,那么每求出一个小问题的解就缓存下来,这样下次再遇到相同的小问题就不用重复计算。另一个实现动态规划算法的方法是按照从下往上的顺序,从解决最小的问题开始,并把已经解决的小问题的解存储下来(大部分面试题都存储在一维数组或二维数组中),然后把小问题的解组合起来逐步解决大问题。
下面通过一个具体的例子来讨论应用动态规划分析和解决问题的过程。
面试题 88 : 爬楼梯的最少成本
题目:
一个数组 cost 的所有数字都是正数,它的第 i 个数字表示在一个楼梯的第 i 级台阶往上爬的成本,在支付了成本 cost[i] 之后可以从第 i 级台阶往上爬 1 级或 2 级。假设台阶至少有 2 级,既可以从第 0 级台阶出发,也可以从第 1 级台阶出发,请计算爬上该楼梯的最少成本。例如,输入数组 [1, 100, 1, 1, 100, 1],则爬上该楼梯的最少成本是 4,分别经过下标 0、2、3、5 这 4 级台阶,如下图所示。

分析:
爬上一个有多级台阶的楼梯自然需要若干步。按照题目的要求,每次爬的时候既可以往上爬 1 级台阶,也可以爬 2 级台阶,也就是每一步都有两个选择。这看起来像是与回溯法相关的问题。但这个问题不是要找出有多少种方法可以爬上楼梯,而是计算爬上楼梯的最少成本,即计算问题的最优解,因此,这个问题更适合运用动态规划。
一、分析确定状态转移方程
这个问题要求计算爬上楼梯的最少成本,可以用函数 f(i) 表示从楼梯的第 i 级台阶再往上爬的最少成本(注意:已经支付了成本 cost[i])。如果一个楼梯有 n 级台阶(台阶从 0 开始计数,从第 0 级一直到第 n - 1 级),由于一次可以爬 1 级或 2 级台阶,因此最终可以从第 n - 2 级台阶或第 n - 1 级台阶爬到楼梯的顶部,即 f(n - 1) 和 f(n - 2) 的最小值就是这个问题的最优解。
应用动态规划的第 1 步是找出状态转移方程,即用一个等式表示其中某一步的最优解和前面若干步的最优解的关系。根据题目的要求,可以一次爬 1 级或 2 级,既可以从第 i - 1 级台阶爬上第 i 级台阶,也可以从第 i - 2 级台阶爬上第 i 级台阶,因此,从第 i 级台阶往上爬的最少成本应该是从第 i - 1 级台阶往上爬的最少成本和从第 i - 2 级台阶往上爬的最少成本的较小值再加上在第 i 级台阶往上爬的成本。这个关系可以用状态转移方程表示为 f(i) = min(f(i - 1), f(i - 2)) + cost[i]。
上述状态转移方程有一个隐含的条件,即 i 大于或等于 2。如果 i 等于 0,则可以直接从第 0 级台阶往上爬,f(0) 等于 cost[0];如果 i 等于 1,也可以直接从第 1 级台阶往上爬,f(1) 等于 cost[1]。
二、递归代码
状态转移方程其实是一个递归的表达式,可以很方便地将它转换成递归代码,如下所示:
class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {int n = cost.size();return min(f(cost, n - 1), f(cost, n - 2));}
private:int f(vector<int>& cost, int i) {if (i < 2)return cost[i];return min(f(cost, i - 1), f(cost, i - 2)) + cost[i];}
};在上述代码中,递归函数 f 和状态转移方程相对应,根据从第 i - 1 级台阶和第 i - 2 级台阶往上爬的最少成本求从第 i 级台阶往上爬的最少成本。
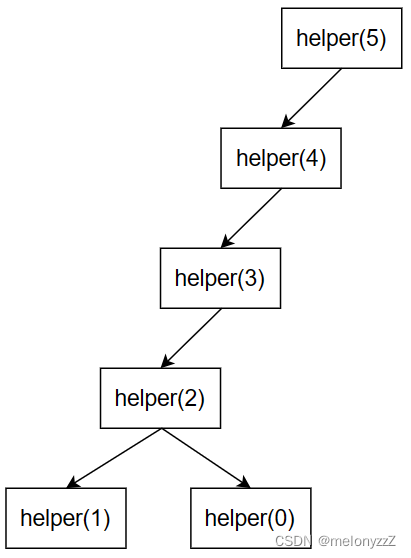
上述代码看起来很简捷,但时间效率非常糟糕。时间效率是面试官非常关心的问题,如果应聘者的解法的时间效率糟糕则很难通过面试。根据前面的递归代码,为了求得 f(i) 需先求得 f(i - 1) 和 f(i - 2)。如果将求解过程用一个树形结构表示(如下图中求解 (9) 的过程),就能发现在求解过程中有很多重复的节点。
求解 f(i) 这个问题的解,依赖于求解 f(i - 1) 和 f(i - 2) 这两个子问题的解,由于求解 f(i - 1) 和 f(i - 2) 这两个子问题有重叠的部分,如果只是简单地将状态转移方程转换成递归的代码就会带来严重的效率问题,因为重复计算是呈指数级增长的。
三、使用缓存的递归代码
为了避免重复计算带来的问题,一个常用的解决办法是将已经求解过的问题的结果保存下来。在每次求解一个问题之前,应先检查该问题的求解结果是否已经存在。如果问题的求解结果已经存在,则不再重复计算,只需要从缓存中读取之前求解的结果。
class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {int n = cost.size();vector<int> dp(n, 0);dp[0] = cost[0]; // 考虑 n == 2 的情况helper(cost, dp, n - 1);return min(dp[n - 1], dp[n - 2]);}
private:void helper(vector<int>& cost, vector<int>& dp, int i) {if (i < 2){dp[i] = cost[i];}else if (dp[i] == 0){helper(cost, dp, i - 1);helper(cost, dp, i - 2);dp[i] = min(dp[i - 1], dp[i - 2]) + cost[i];}}
};在上述代码中,数组 dp 用来保存求解每个问题结果的缓存,dp[i] 用来保存 f(i) 的计算结果。该数组的每个元素都初始化为 0。由于题目中从每级台阶往上爬的成本都是正数,因此如果某个问题 f(i) 之前已经求解过,那么 dp[i] 的缓存的结果将是一个大于 0 的数值。只有当 dp[i] 等于 0 时,它对应的 f(i) 之前还没有求解过。
有了这个缓存 dp,就能确保每个问题 f(i) 只需求解一次。如果楼梯有 n 级台阶,那么上述代码的时间复杂度是 O(n)。同时,需要一个长度为 n 的数组,因此空间复杂度也是 O(n)。
前面的递归解法都是从大问题入手的,将问题 f(i) 分解成两个子问题 f(i - 1) 和 f(i - 2)。这种从大问题入手的过程是一种自上而下的求解过程。
四、空间复杂度为 O(n) 的迭代代码
也可以自下而上地解决这个过程,也就是从子问题入手,根据两个子问题 f(i - 1) 和 f(i - 2) 的解求出 f(i) 的结果。通常用迭代的代码实现自下而上的求解过程,如下所示:
class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {int n = cost.size();vector<int> dp(n);dp[0] = cost[0], dp[1] = cost[1];for (int i = 2; i < n; ++i){dp[i] = min(dp[i - 1], dp[i - 2]) + cost[i];}return min(dp[n - 1], dp[n - 2]);}
};显然,这种解法的时间复杂度和空间复杂度都是 O(n)。
五、空间复杂度为 O(1) 的迭代代码
上述迭代代码还能做进一步的优化。前面用一个长度为 n 的数组将所有 f(i) 的结果都保存下来。求解 f(i) 时只需要 f(i - 1) 和 f(i - 2) 的结果,从 f(0) 到 f(i - 3) 的结果其实对求解 f(i) 并没有任何作用。也就是说,在求解每个 f(i) 的时候,需要保存之前的 f(i) 和 f(i - 2) 的结果,因此只要一个长度为 2 的数组即可。
class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {int n = cost.size();vector<int> dp(2);dp[0] = cost[0], dp[1] = cost[1];for (int i = 2; i < n; ++i){dp[i % 2] = min(dp[0], dp[1]) + cost[i];}return min(dp[0], dp[1]);}
};优化之后的代码的时间复杂度仍然是 O(n),空间复杂度是 O(1)。