文章目录
- 1. 问题
- 2. 输入
- 3. 输出
- 4. 示例
- 5. 分析
- 6. 思路
- 7. 数论,取模相关公式
- 8. 数论,同余定理
- 9. 代码
1. 问题
小强发现当已知 x y = B xy=B xy=B以及 x + y = A x+y=A x+y=A时,能很轻易的算出 x n x_ {n} xn + y n y_ {n} yn 的值.但小强想请你在已知A和B的情况下,计算出 x + y x+y x+y的值.因为这个结果可能很大所以所有的运算都在模1e9+7下进行.
2. 输入
第一行输入一个正整数T.表示有T组数据
接下来T行, 每行输入三个整数A,B和n
1 < = T < = 100 0 < = A , B < = 1 e 9 + 7 1 < = n < = 1 e 5 1<=T<=100\\ 0<=A,B<=1e9+7\\ 1<=n<=1e5 1<=T<=1000<=A,B<=1e9+71<=n<=1e5
3. 输出
输出 T T T行,每一行表示每组数据的结果.
4. 示例
输入例子:
3
4 4 3
2 3 4
5 2 6
输出例子:
16
999999993
9009
5. 分析
本题实际上就是个数学问题,积累了递推公式雀氏很好做,否则就很操蛋
递推公式
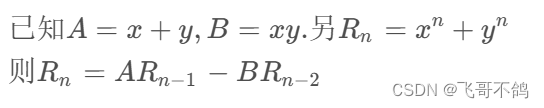
证明
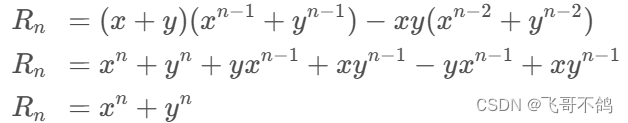
6. 思路
迭代计算,类似斐波那契。不过需要小心溢出问题。本题中,A、B的值可能不会很大,但A、B计算处理后得到的值溢出的概率极高。如果A、B均为int,那么计算时就极容易发生溢出现象,因此A、B类型设置为long
此外,最终结果需要取模,笔者额外介绍一下数论中有关取模的信息
7. 数论,取模相关公式
(a + b) % p = (a%p + b%p) %p
(a - b) % p = ((a%p - b%p) + p) %p
(a * b) % p = (a%p)*(b%p) %p
详细介绍的文章
- 快速幂取模
- 快速乘法取模
快速求模,其实就是运用到了取模的性质,把大的数字分部拆解为小的数字。当然拆的过程中会出现各种细节
一句话总结:拆出来的数字,都取模。切记除法、指数不要这么做
8. 数论,同余定理
如果(a - b)能够被m整除,即m | (a - b),那么a mod m = b mod m。我们称称整数a与b对模m同余,记作a≡b(mod m)
这个也好理解,a - b能够被m整除,说明a,和b mod m能够得到相同余数,只有这样,a - b才能把多余的数字去除,因此a - b才能被m整除
详细介绍的文章
- 同余定理
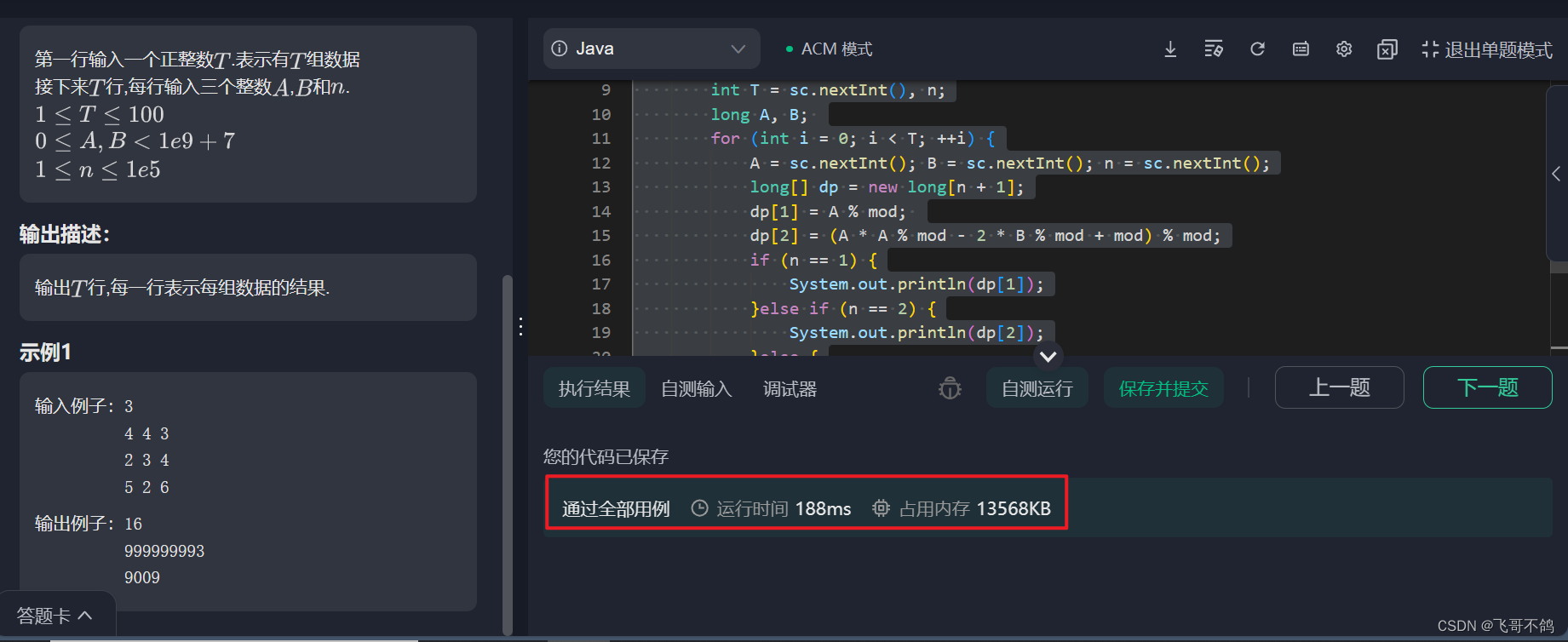
9. 代码
import java.util.*;// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {static final int mod = 1000000000 + 7;public static void main(String[] args) {Scanner sc = new Scanner(System.in);int T = sc.nextInt(), n;long A, B; for (int i = 0; i < T; ++i) {A = sc.nextInt(); B = sc.nextInt(); n = sc.nextInt();long[] dp = new long[n + 1];dp[1] = A % mod; // 为了防止溢出,注意取模。具体公式上文有讲dp[2] = (A * A % mod - 2 * B % mod + mod) % mod;if (n == 1) {System.out.println(dp[1]);}else if (n == 2) {System.out.println(dp[2]);}else {for (int j = 3; j <= n; ++j) {dp[j] = (A * dp[j - 1] % mod - B * dp[j - 2] % mod + mod) % mod;}System.out.println(dp[n]);}}}
}