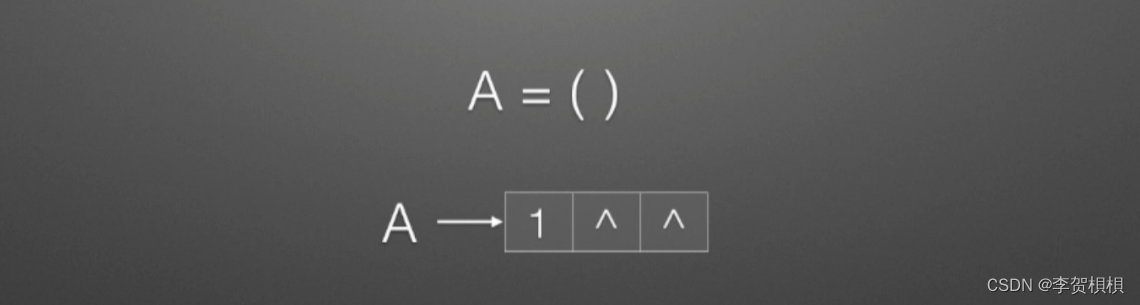第一章 逻辑结构

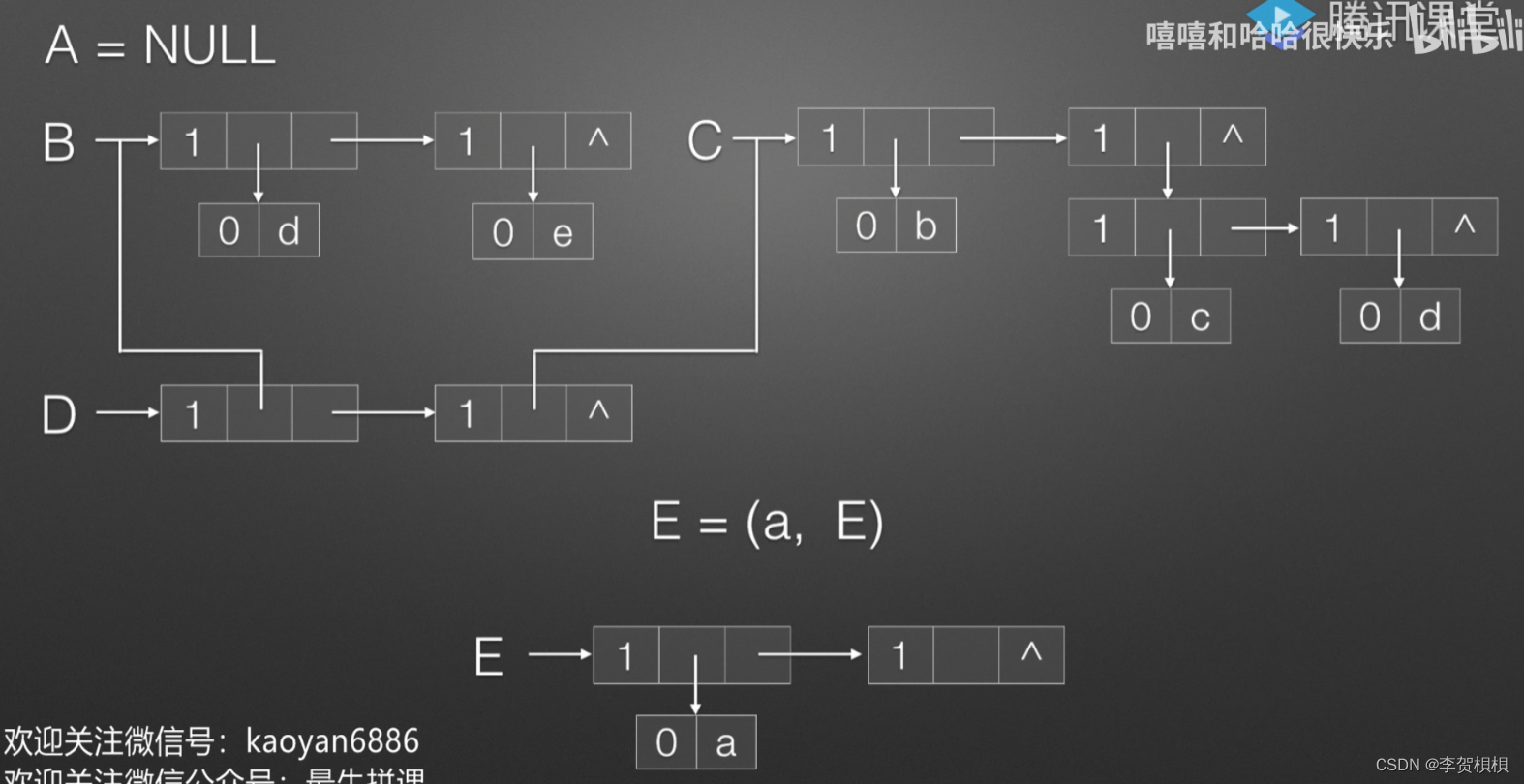
（1）A=()，A是一个空表，长度为0，深度为1。
（2）B=(d,e)，B的元素全是原子，d和e，长度为2，深度为1。
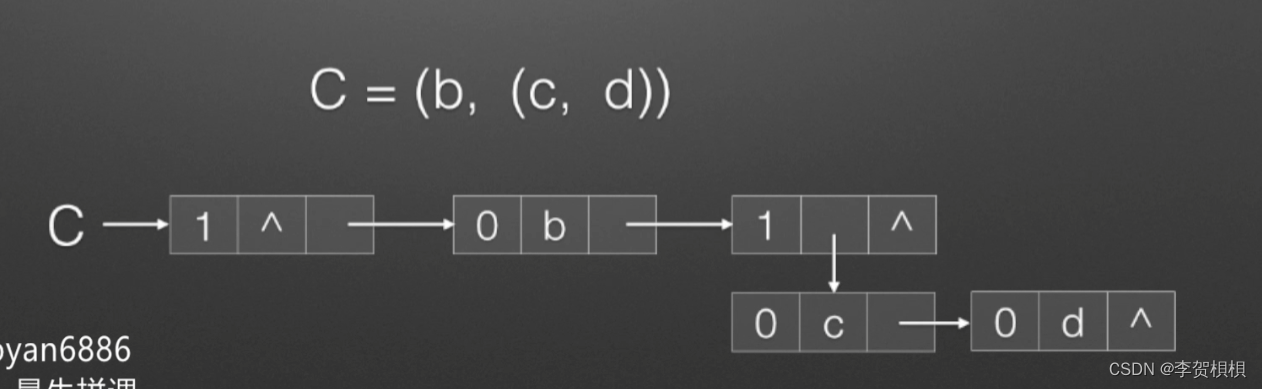
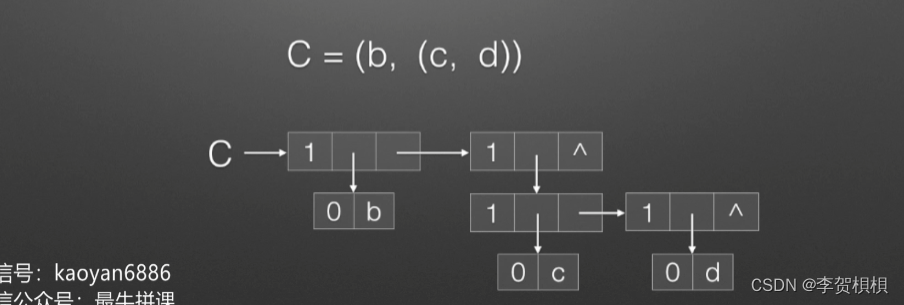
（3）C=(b,(c,d))，C有两个元素，分别是原子b和另一个广义表(c,d)，长度为2，深度为2。
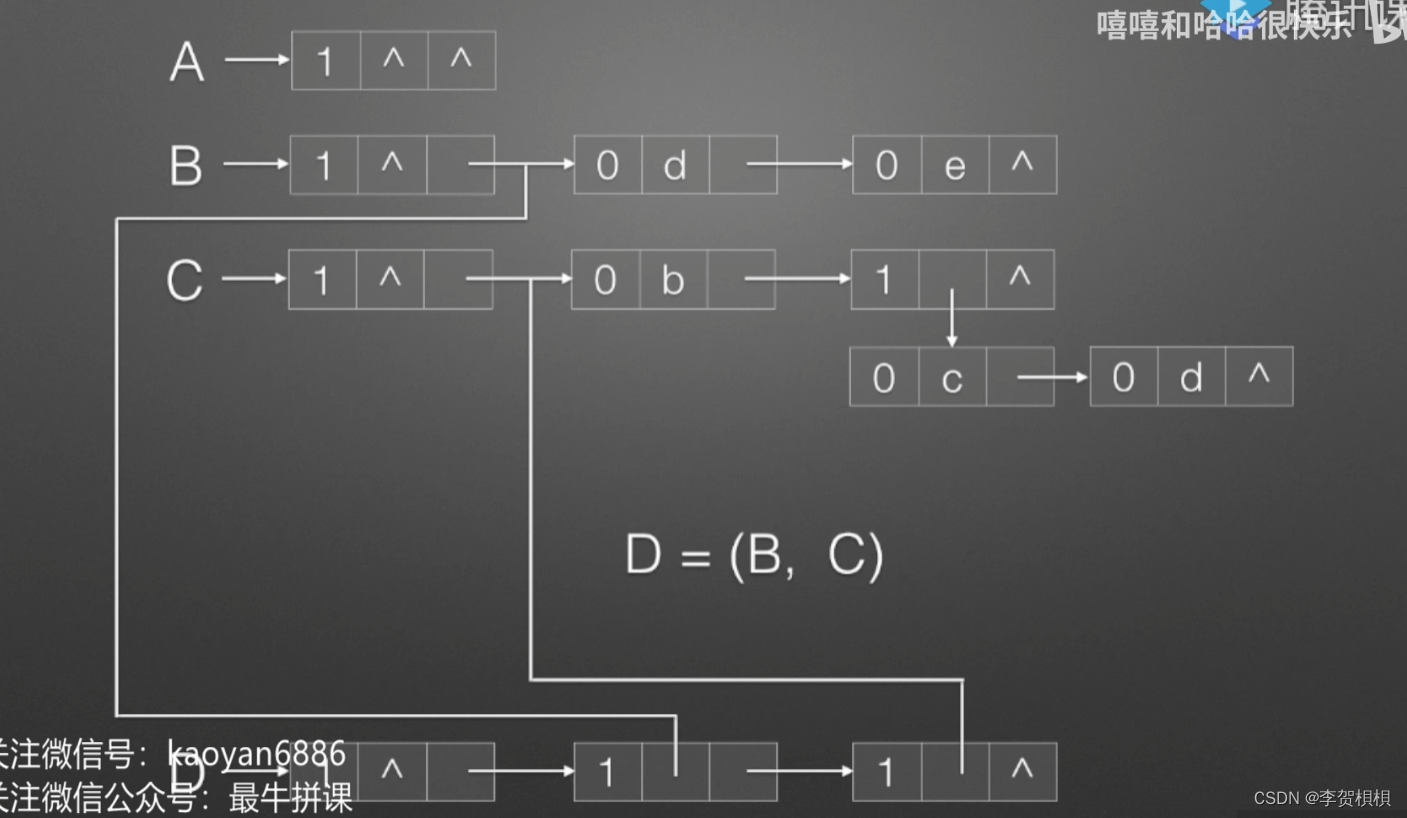
（4）D=(B,C)，D的元素全是广义表，B和C，长度为2，深度为3，由此可见一个广义表的子表可以是其他已经定义好的广义表的引用。
（5）E=(a,E)，E有两个元素，原子a和它本身，长度为2，由此可见一个广义表可以是递归定义的。展开E可以得到(a,(a,(a,(a,…))))，是一个无限深的广义表。

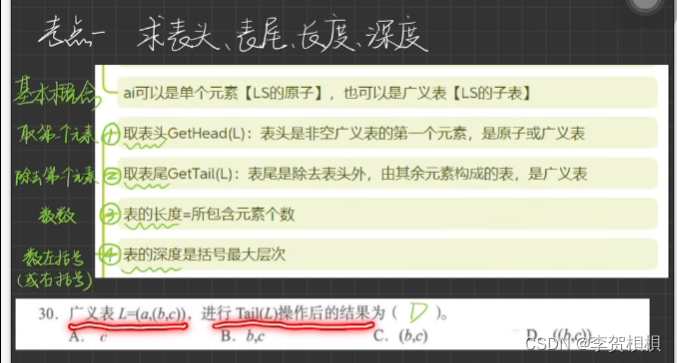
广义表的长度：为表中最上层元素的个数。如广义表的C长度为2，注意不是3。

广义表的深度：为表中括号的最大层数。求深度时可将子表展开，如广义表D应该展开为((d,e),(b,(c,d)))，深度为3。

表头(Head)和表尾(Tail)：当广义表非空时，第一个元素为广义表的表头，其余元素组成的表是广义表的表尾。
例如：

//GetTail一定是一个广义表，必须有()
GetHead(D)=B; 
GetTail(D)=(C); 
GetHead((a))=a; 
GetTail((a))=();

第二章 存储结构

2.1 头尾链表存储结构

2.2 扩展线性表存储结构