面试经典150题【91-100】

五道一维dp题+五道回溯题。

70.爬楼梯

从递归到动态规划

    public int climbStairs(int n) {if(n==0) return 1;if(n==1) return 1;if(n==2) return 2;return climbStairs(n-1) + climbStairs(n-2);}

这样会超时，然后把他放到数组里。

public int climbStairs(int n) {int[]ans = new int[n+1];ans[0]=1;ans[1]=1;for(int i=2;i<n+1;i++){ans[i]=ans[i-1] + ans[i-2];}return ans[n];}

然后你也可以将数组再简化为两个变量。因为只与前两个变量有关。

198.打家劫舍

class Solution {public int rob(int[] nums) {if(nums.length == 0) return 0;int N=nums.length;int[] dp=new int[N+1];dp[0]=0;dp[1]=nums[0];for(int i=2;i<N+1;i++){// 第2家 dp[2], 不偷dp[1],  偷 dp[0]+nums[1]dp[i]=Math.max(nums[i-1]+dp[i-2],dp[i-1]);}return dp[N];}
}

一维dp的子问题，基本就是与dp[i-1]和dp[i-2]有关系。

139.单词拆分

class Solution {public boolean wordBreak(String s, List<String> wordDict) {Set<String> wordDictSet = new HashSet(wordDict);int maxLen=0;for(String str:wordDictSet){maxLen = Math.max(maxLen,str.length());}boolean[] dp=new boolean[s.length() +1];dp[0]=true;for(int i=0;i<s.length()+1;i++){for(int j=Math.max(0,i-maxLen);j<i;j++){if(dp[j] && wordDictSet.contains(s.substring(j,i))){dp[i]=true;break;}}}return dp[s.length()];}
}

dp[i]代表从0到i这个字符串成不成。

322.零钱兑换

做一个长度为amount +1 的数组，每个位置代表着i能不能被硬币拼凑。
要注意初始化dp[0]=0

class Solution {public int coinChange(int[] coins, int amount) {int[] dp=new int[amount+1];Arrays.fill(dp,amount+1);dp[0]=0;for(int i=0;i<amount+1;i++){for(int j=0;j<coins.length;j++){if(i-coins[j]>=0)dp[i] = Math.min(dp[i],1+dp[i-coins[j]]);}}return dp[amount]>amount? -1:dp[amount];}
}

300.递增最长子序列

class Solution {public int lengthOfLIS(int[] nums) {//dp[i] 为必须包含第 i 个元素的最长递增子序列int[] dp=new int[nums.length];Arrays.fill(dp,1);for(int i=0;i<nums.length;i++){for(int j=0;j<i;j++){if(nums[i]>nums[j]){dp[i]=Math.max(dp[i],dp[j]+1);}}}int ans=0;for(int i=0;i<nums.length;i++){ans=Math.max(ans,dp[i]);}return ans;}
}

77.组合

画一个递归的树图

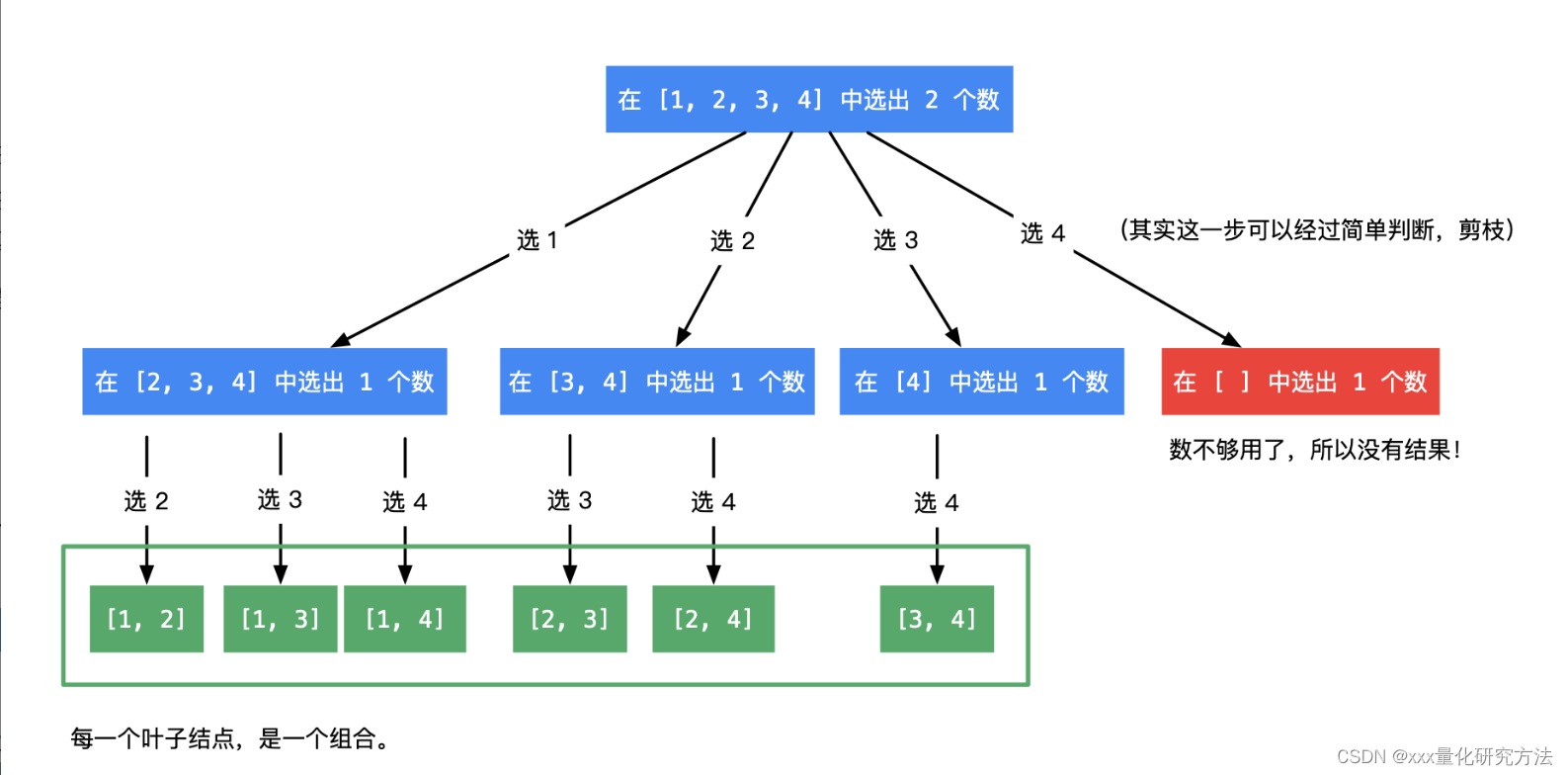
class Solution {public List<List<Integer>> combine(int n, int k) {List<List<Integer>> res = new ArrayList<>();if (k <= 0 || n < k) {return res;}// 从 1 开始是题目的设定Deque<Integer> path = new ArrayDeque<>();dfs(n, k, 1, path, res);return res;}private void dfs(int n, int k, int begin, Deque<Integer> path, List<List<Integer>> res) {//终止条件是path的长度等于kif(path.size() == k){res.add(new ArrayList<>(path));return ;}//以i开头，n结尾for(int i=begin;i<=n;i++){path.addLast(i);dfs(n,k,i+1,path,res);path.removeLast();}}}

或者换一个树的类型，选与不选。只修改dfs即可

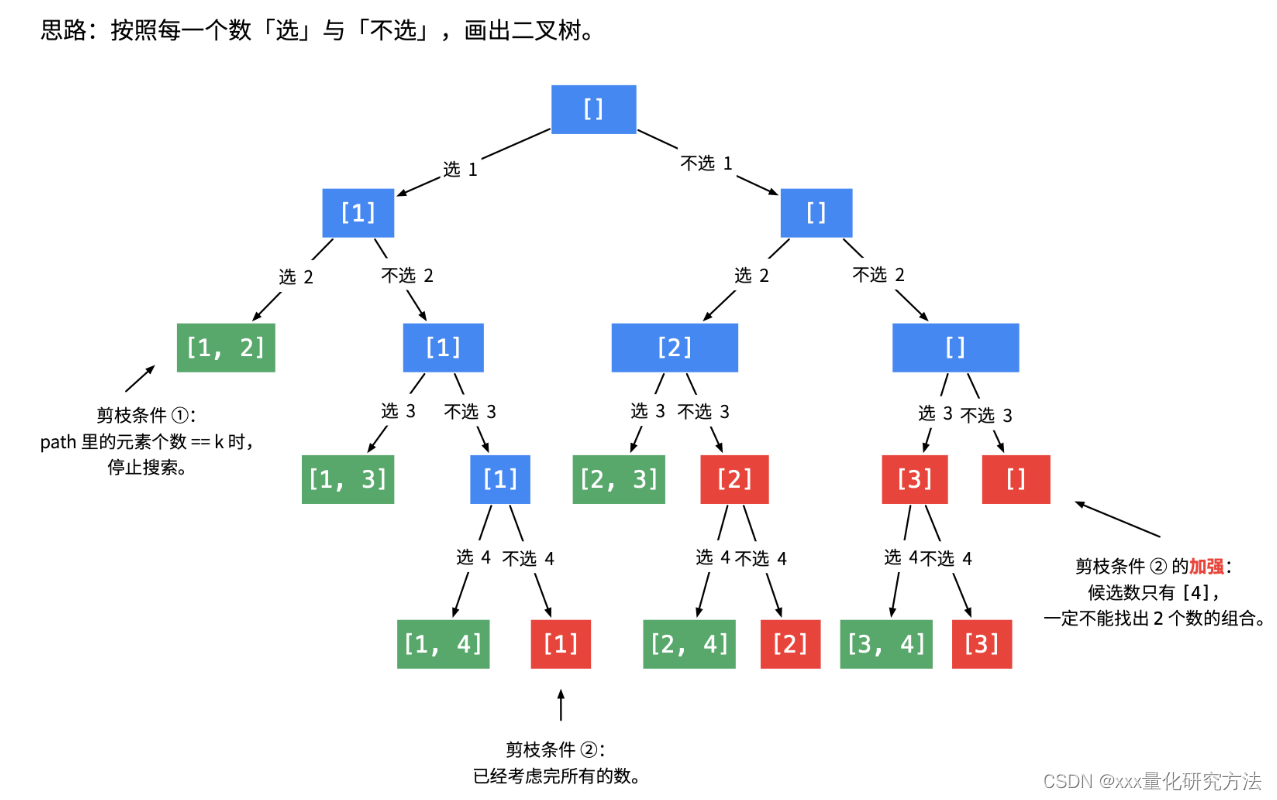
class Solution {public List<List<Integer>> combine(int n, int k) {List<List<Integer>> res = new ArrayList<>();if (k <= 0 || n < k) {return res;}// 从 1 开始是题目的设定Deque<Integer> path = new ArrayDeque<>();dfs(n, k, 1, path, res);return res;}private void dfs(int n, int k, int begin, Deque<Integer> path, List<List<Integer>> res) {//终止条件是path的长度等于kif(path.size() == k){res.add(new ArrayList<>(path));return ;}if(begin == n+1){return ;}//不加新元素dfs(n,k,begin+1,path,res);//添加新元素path.addLast(begin);dfs(n,k,begin+1,path,res);path.removeLast();}}

要对begin也做限制。
总体的板子还是。做一个helper函数，终止条件，dfs,这一步要加的，dfs,减去这一步加的。

46.全排列

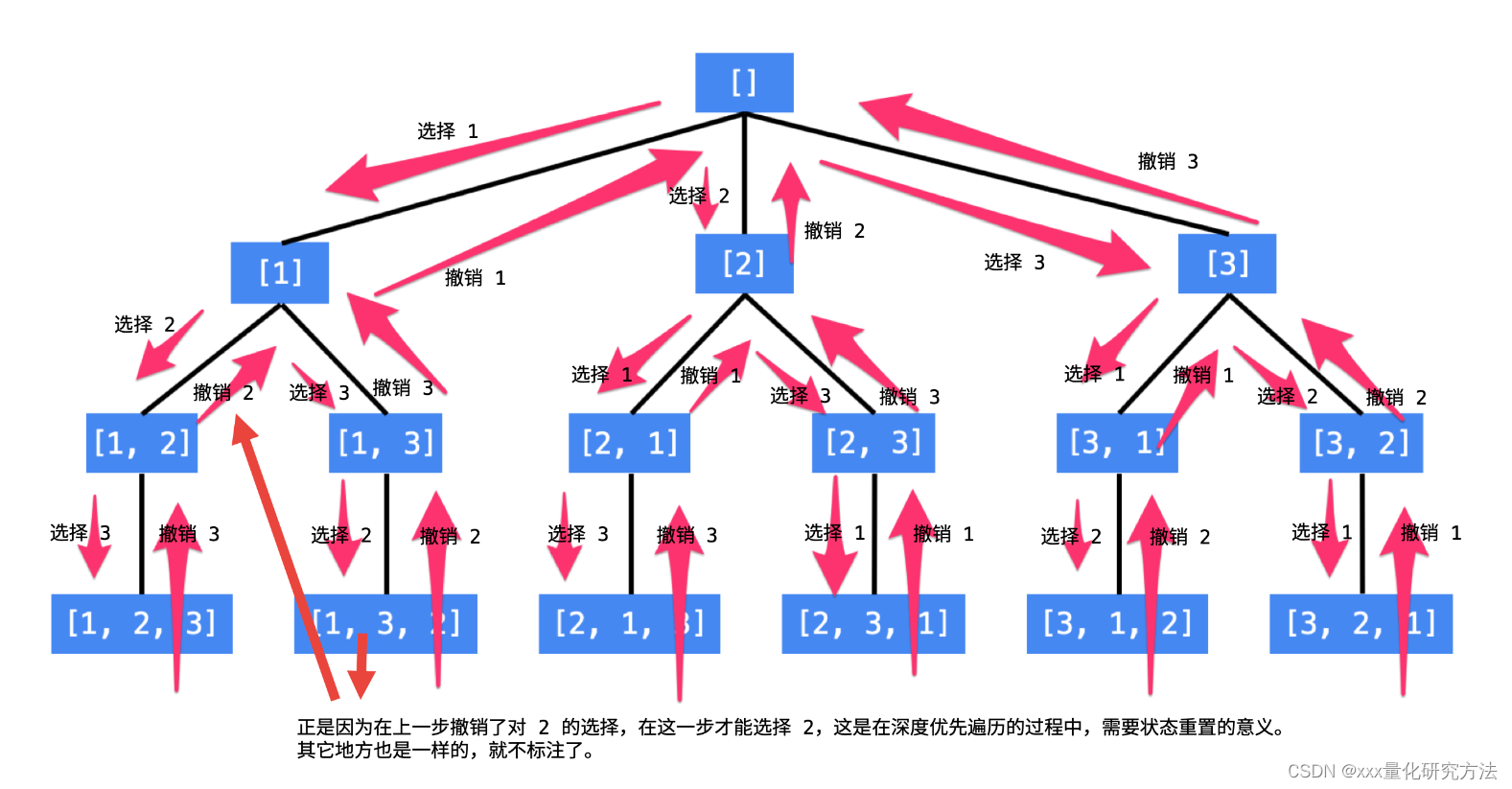
class Solution {public List<List<Integer>> permute(int[] nums) {int len=nums.length;List<List<Integer>> res=new ArrayList<>();if(len == 0) return res;boolean[] used=new boolean[len];List<Integer> path=new ArrayList<>();dfs(nums,len,0,path,used,res);return res;}private void dfs(int[] nums, int len, int depth,List<Integer> path, boolean[] used,List<List<Integer>> res) {if(depth == len){res.add(new ArrayList<>(path));return;}for(int i=0;i<len;i++){if(!used[i]){path.add(nums[i]);used[i]=true;dfs(nums, len, depth + 1, path, used, res);used[i]=false;path.remove(path.size()-1);}}}
}

要用一个used数组记录哪个位置被使用。

39.组合总和（※）

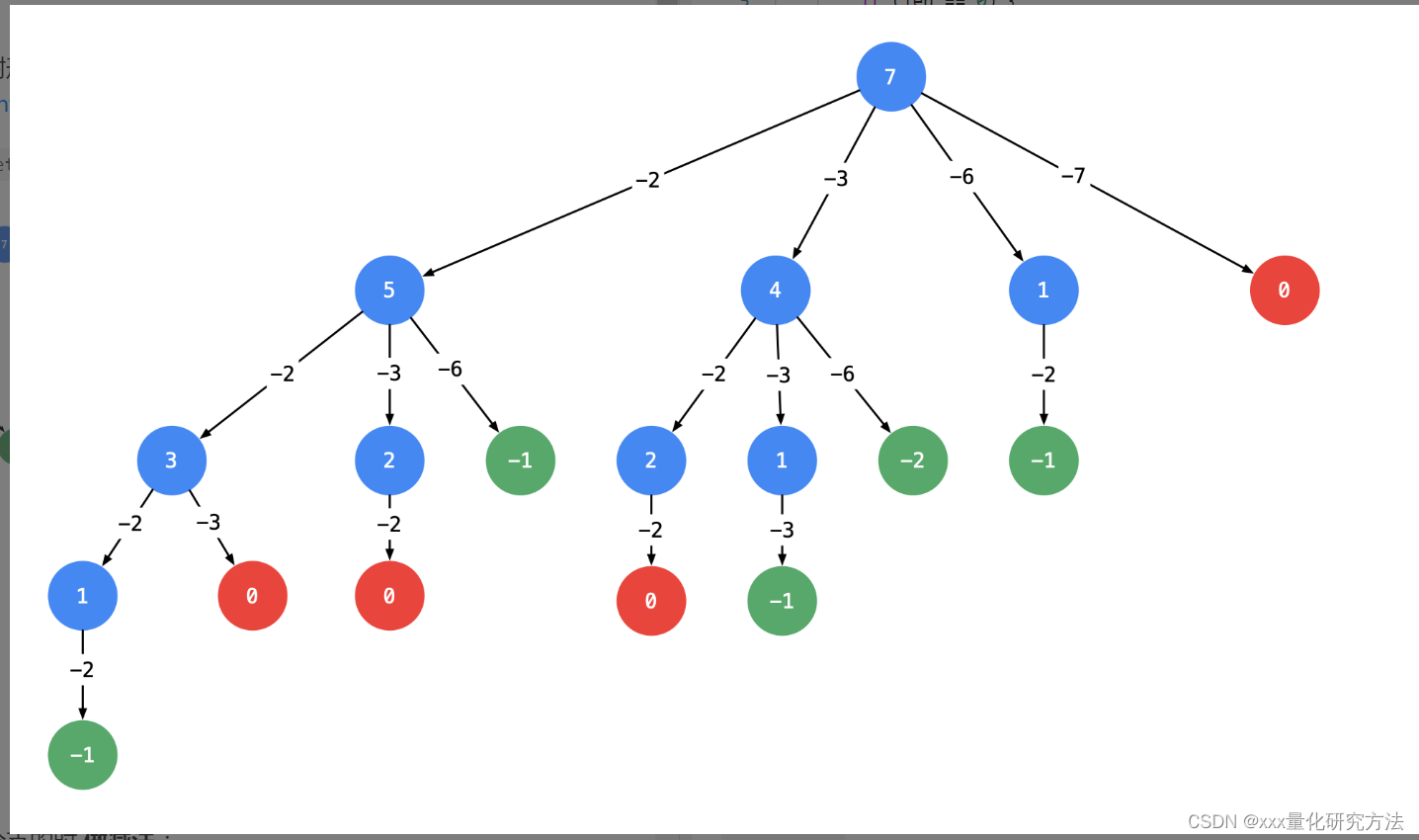
class Solution {public static List<List<Integer>> combinationSum(int[] candidates, int target) {int len = candidates.length;List<List<Integer>> res = new ArrayList<>();if (len == 0) {return res;}// 排序是剪枝的前提Arrays.sort(candidates);Deque<Integer> path = new ArrayDeque<>();dfs(candidates, 0, len, target, path, res);return res;}public static void dfs(int[] candidates,int begin,int len,int target,Deque<Integer>path,List<List<Integer>> res){if (target == 0) {res.add(new ArrayList<>(path));return;}for(int i=begin;i<len;i++){if(target-candidates[i] <0) break;path.addLast(candidates[i]);dfs(candidates,i,len,target-candidates[i],path,res);path.removeLast();}}
}

注意dfs中的i , 从begin到len , 并且也要传递到下一个dfs中去。

• 排列问题，讲究顺序（即 [2, 2, 3] 与 [2, 3, 2] 视为不同列表时），需要记录哪些数字已经使用过，此时用 used 数组；

• 组合问题，不讲究顺序（即 [2, 2, 3] 与 [2, 3, 2] 视为相同列表时），需要按照某种顺序搜索，此时使用 begin 变量。

22.括号生成

class Solution {public static List<String> generateParenthesis(int n) {List<String> res = new ArrayList<>();String cur = "";int left = 0, right = 0;dfs(res, cur, n, left, right);return res;}public static void dfs(List<String> res, String cur, int n, int left, int right) {if (left > n || left < right)return;if (cur.length() == 2 * n) {res.add(cur);}if (left < n)dfs(res, cur + "(", n, left + 1, right);if (right < n)dfs(res, cur + ")", n, left, right + 1);}
}

这种是直接将修改的新字符串传递给函数。

public class LC22 {public static List<String> generateParenthesis(int n) {List<String> res=new ArrayList<>();StringBuilder sb=new StringBuilder();int left=0,right=0;dfs(res,sb,n,left,right);return res;}public static void dfs(List<String> res,StringBuilder sb,int n,int left,int right){if(left >n || left<right) return;if(sb.length()== 2*n && left ==n){res.add(sb.toString());return;}if(left<n){sb.append("(");dfs(res,sb,n,left+1,right);sb.deleteCharAt(sb.length()-1);}if(right<n){sb.append(")");dfs(res,sb,n,left,right+1);sb.deleteCharAt(sb.length()-1);}}public static void main(String[] args) {System.out.println(generateParenthesis(3));}
}

这种就是很典型的回溯了，增加了再删除。

79.单词搜索

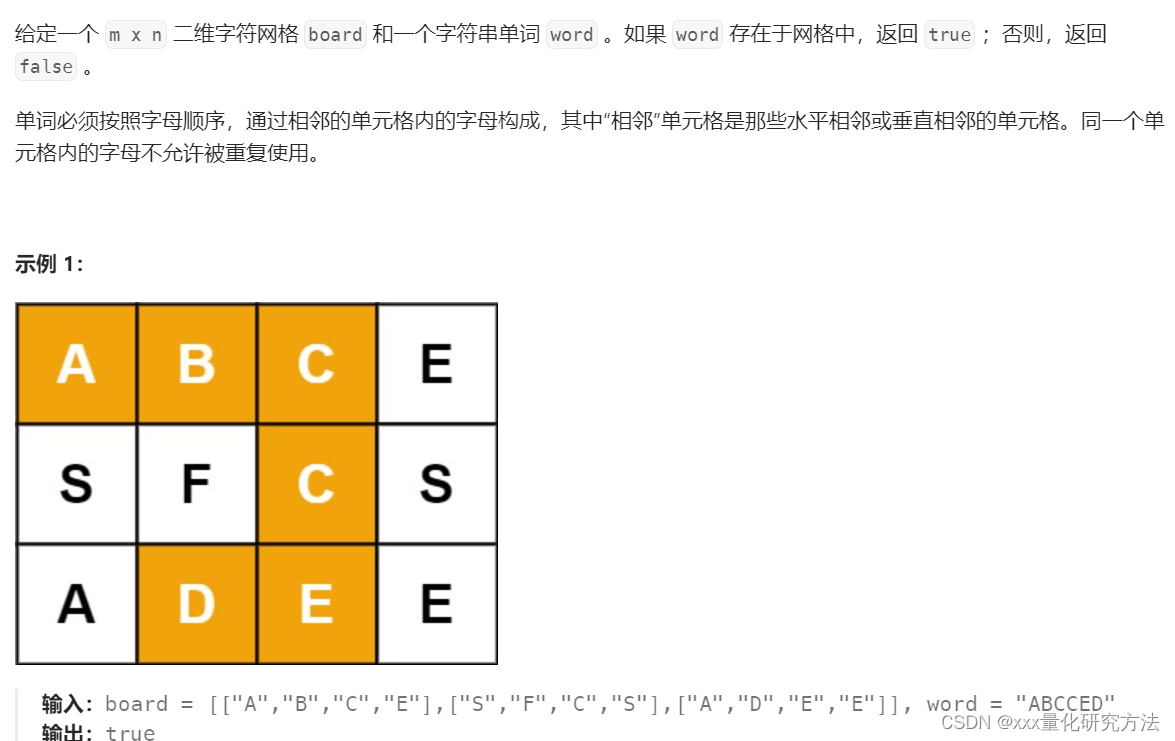
以每一个字母为开头进行搜索。搜索过程就是dfs的上下左右。
遍历到成功后要置为’\0’,这样可以防止第二次遍历到，结束了要改回来。
k代表遍历到word字符串的哪个变量了

public class LC79 {public boolean exist(char[][] board, String word) {char[] words = word.toCharArray();for(int i = 0; i < board.length; i++) {for(int j = 0; j < board[0].length; j++) {if (dfs(board, words, i, j, 0)) return true;}}return false;}public boolean dfs(char[][] board, char[] word, int i, int j, int k) {if (i < 0 || j < 0 || i > board.length - 1 || j > board[0].length - 1 || board[i][j] != word[k]) return false;if (k == word.length - 1) return true;board[i][j] = '\0';boolean ans = dfs(board, word, i + 1, j, k + 1) || dfs(board, word, i - 1, j, k + 1) ||dfs(board, word, i, j - 1, k + 1) || dfs(board, word, i, j + 1, k + 1);board[i][j] = word[k];return ans;}
}