本篇很高能，如有错误欢迎指出，本人能力有限（需要前置知识记忆化dfs，树形dp，bfs+dp，tarjan）

另外，本篇之所以属于图论，也是想让各位明白，dfs就是就是在跑图！如果dfs离开了图论的知识将会困难重重

记忆化dfs可以看这里

【算法每日一练]-记忆化dfs （保姆级教程 篇4）#滑雪 #天下 第一 #切木棍-CSDN博客

树形dp可以看这里

【算法每日一练]-动态规划 （保姆级教程 篇6（树形dp））-CSDN博客

tarjan可以看这里（这个是重点）

【看不懂你来打我]-图论（保姆级教程篇11 tarjan）无向图的桥 ，无向图的割点 ，有向图的强连通分量-CSDN博客

        

先来题目引出问题：

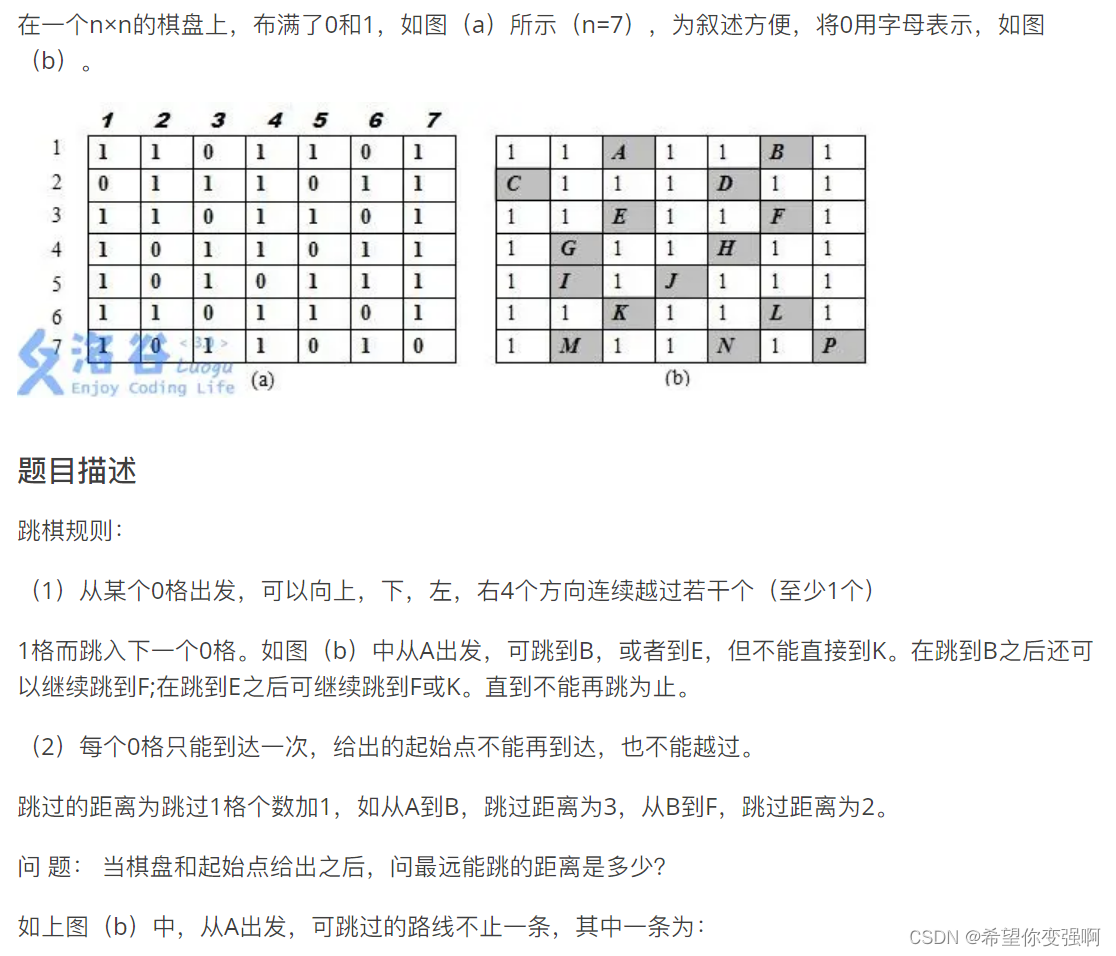
题目：跳棋

         

碎碎念部分：（如果你有兴趣可以看一下，如有错误欢迎指出，本人能力有限）

题意就是从0的地方选四个方向，跳到下一个0的地方，重复，问问你最远能走多远？

那么我就寻思好嘛，太常见了：我反手就是f[x][y]=max(dfs[下一个0坐标]+当前0坐标到下一个0坐标的距离)，然后设置f[x][y]表示从当前点出发能走的最远距离。这样的话还能记忆化加速，我去，我可太聪明了！下面是我的伪代码：

for（4个方向）
{   先获取该方向下一个0点坐标；if（该坐标存在且该坐标并没有走过）{   vis[下个坐标]=1；d=dfs（下一个坐标）+两点坐标距离；vis[下个坐标]=0;if（f[x][y]<d）f[x][y]=d;}}
}

然后外面的dfs再加上记忆化和返回值步骤即可。欧了，输入样例---------跑的什么玩意？？？

        

其实这段代码问题很大！

首先就是vis数组和dfs(下个状态)非常冲突，因为你设置的f[x][y]表示以此为起点去跑，可是你在dfs下一个状态时候的它的vis都不是清空的，它的返回的f结果怎么可能会是对的呢？想要使得下一个状态的结果是正确的就应该让它以起点单独跑，你以为这样就行了？

还是错！因为它的下一个状态还会遇到相同的问题，那么返回的结果也不对，（那不无解了吗）

还有一点是记忆化那里：if(f[此状态来过])return f[此状态]。

这句话也不对，因为它的前提是你的f状态的结果是正确的，如果现在还不是正确的，那不应该继续跑它吗？而不是直接去使用呀，所以这句话也不能有！

以上的思路都是来自之前做过的一道滑雪的题。（在开头哪里有，你可以去看一看）

然后我们来对比一下之前做过的“ 滑雪 ”那道记忆化题：

在那个题中，我们设置f[x][y]表示从此点为起点跑的最远距离，然后有f[x][y]=max(f[x][y],dfs(下一个点)+1)，之所以这个式子是正确的，是因为它后面的dfs(下一个点）的结果是正确的！那为什么下一个点的dfs是正确的呢？是因为它下一个dfs的结果是正确的，那么为什么它下一个结果是也是正确的呢？是因为它每个下层状态都不依赖于前面的dfs结果，也就是没有环！也正因为没有环，这个dfs的结果一定是正确的。也就是不会改变的，既然都不会再改变，那以后再遇到这种情况还跑啥呀直接使用结果呗，所以就可以记忆化去省时间，它的模式是类似树形dp的，就是不会遇到环。

到这里，你就发现了本题出问题的原因是有环！也就是你的下一个状态要想正确的跑出来，就依赖于之前的状态，但是之前状态的正确性又要靠后面去跑，所以这样去设置f[x][y]的含义是非常不应该的。所有有环的dp都非常危险，无论是你是循环dp还是dfsdp，都不是很妥的。而树形dfs一般都可以来dp，也可以记忆化。

另外，递推一般可以记忆化，搜索当然也可以记忆化，而有环一般就不行了。当然有环一般伴随着回溯。

说了这么多。赶紧回来回来

思路：

本题明显适合搜索，而不是递推。

我们可以直接去搜索跑的，并不会超时，每dfs一个点就先更新一下答案，然后找到下一个0点坐标，如果有的话且没有走过就跳过去，然后从那个点继续跑，回来时候再清空标记。重复。

一套流程行云流水就打出来了。代码如下：

#include <bits/stdc++.h>
using namespace std;
int n,k,ans;
int m[105][105],f[105][105];//f来标记是否来过
int dx[]={-1,1,0,0},dy[]={0,0,1,-1};
void dfs(int x,int y,int step){ans=max(ans,step);//更新答案for(int i=0;i<4;i++){int tx=x,ty=y,s=0;while(tx+dx[i]>0&&tx+dx[i]<=n&&ty+dy[i]>0&&ty+dy[i]<=n){tx+=dx[i];ty+=dy[i];//不断沿着这个向量前进s++;//获取两点距离，注意至少超越一下，s最少是2！if(m[tx][ty]==0)break;}if(tx>0&&tx<=n&&ty<=n&&ty>0&&f[tx][ty]==0&&m[tx][ty]==0&&s!=1){f[tx][ty]=1;dfs(tx,ty,step+s);//搜下一个点f[tx][ty]=0;}}
}
int main(){int x,y;cin>>n>>x>>y;for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)cin>>m[i][j];f[x][y]=1;//标记出发点被走过了dfs(x,y,0);//开始搜索cout<<ans<<'\n';return 0;	
}

 

        

        

 题目：奶牛隔间

        

一开始思路是模拟，后来看到隔间数和奶牛数……好吧不行，那应该就是dp了，循环dp我不太会写，dfsdp应该可以的，好的，那么我们开始写：

设置f[x]表示从x开始访问的隔间数，那么因为从x隔间走，访问的隔间数是一定的，故而可以记忆化节省时间，那么反手就是：

f[x]=dfs(下一个隔间)+1；然后这个式子我是越看越迷糊，下一个隔间要想成功遍历，和上一个状态很冲突啊！因为从下一个隔间为起点的话，当前的隔间x就不能被标记呀，看到了吗？下一个状态会跑到前一个状态，你告诉我这能dp？

思路：

根据题意，一只奶牛停止的条件是来到她所经过过的房间，也就是奶牛想要停下来必须要找到一个环。看到了吧，这是有环的，那么我们也有tarjan啊。来吧！

首先明显是有向图，我们跑一下tarjan把那些环划到一起，然后把环看成一个整体，或者把整个图看成是许多个强连通分量（为什么？因为无论这个环从哪个点进入，返回结果都是一样，都是环长），我们在这些强联通分量之间建立指向关系，然后就可以树形dp了，当然也需要记忆化（不然还是超时）另外提示一下：强联通分量中节点数就是环上点的个数。

#include <bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int num,n,be[N],to[N],out[N],dfn[N],low[N],dp[N],sz[N];
bool ins[N];
stack<int>s;
void tarjan(int u){dfn[u]=low[u]=++num;ins[u]=1;s.push(u);int v=to[u];if(!dfn[v]) tarjan(v),low[u]=min(low[u],low[v]);else if(ins[v]) low[u]=min(low[u],dfn[v]);
//	for(int i=0,sz=ve[u].size();i<sz;i++){//老模版了
//		int v=ve[u][i];
//		if(!dfn[v]){
//			tarjan(v);low[u]=min(low[u],low[v]);
//		}
//		else if(ins[v]){
//			low[u]=min(low[u],dfn[v]);
//		}
//	}if(low[u]==dfn[u]){int v;do{v=s.top();s.pop();be[v]=u;ins[v]=0;sz[u]++;//顺便统计这个环（强联通分量）中有多少个点}while(v!=u);}
}
int dfs(int u){if(u==0||dp[u])return dp[u];//记忆化return dp[u]=dfs(out[u])+sz[u];//树形dp
}
int main(){cin>>n;for(int i=1;i<=n;i++)scanf("%d",&to[i]);for(int i=1;i<=n;i++){if(!dfn[i])tarjan(i);}for(int i=1;i<=n;i++){if(be[i]!=be[to[i]])out[be[i]]=be[to[i]];//因为出边只有一个，所以这样建边}for(int i=1;i<=n;i++)printf("%d\n",dfs(be[i]));return 0;
}

        

        

题目：小A和uim之大逃离 II

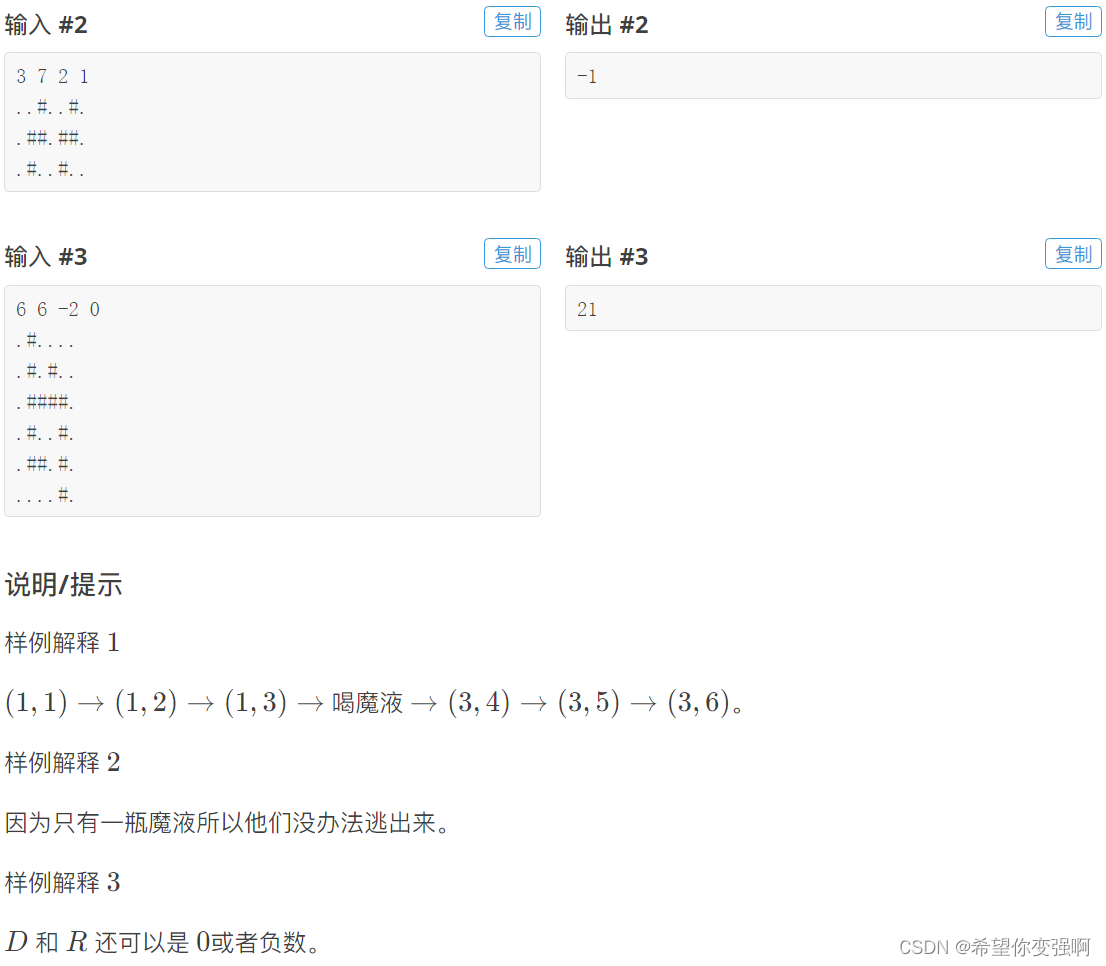
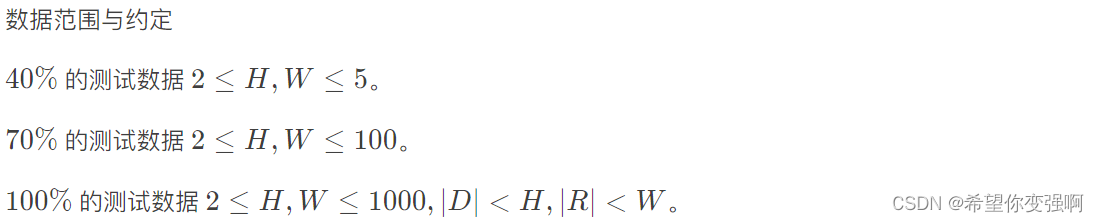
每个点都有两种状态，问你能不能走出去，可能有人想循环dp，但是这个绝对不能循环dp。

因为循环dp的顺序非常有问题，导致在转移的时候有多点还没有更新就已经被转移了，是必错的结局！那么正解是什么呢？

我认为bfs+dp是最好的，因为bfs是按层跑的，dp应该按层去转移，才是最正确的！

思路：

对于本题，每个点都有两种，如果只有一种，那么就很好转移；但是如果有两种，那么不妨就保存两种点。       
我们bfs是按层跑的，不放设置st[x][y][u]表示走到(x,y)点且没有嗑药的最小步数(u=0)，表示走到(x,y)点且已嗑药的最小步数(u=1)。

当从当前点cur.x和cur.y准备走到下个点x，y时：

如果到下一点不嗑药，无论u是0还是1，那么都是st[x][y][cur.u]=st[cur.x][cur.y][cur.u]+1。然后入队
如果到下一点再嗑药，那么就是st[x+d][y+r][1]=st[x][y][0]+1。然后入队

千万注意顺序，一定是先不嗑药在前面，把st[x][y][0]更新正确，然后才是考虑这个点嗑药。你当然可以理解成嗑药的话相当于走了两步！（也没有人说bfs的所有点都只能一次走一步啊）

补充：

你会发现这些转移都是具有唯一性的，也就是说仅转移一次。
直观理解：上面是不嗑药的平面点集，u全是0，下面是嗑药的平面点集，u全是1。在跑bfs的时候，我们允许发生点从上面跑到下面，但是不能从下面到上面。
而且下面的点要么是由前面转移过来，要么是从上面点转移过来，只有这两种情况，同时分别对应不嗑药和嗑药。至此，bfs+dp验证成立！

#include <bits/stdc++.h>
using namespace std;
const int N=1005;
int h,w,d,r,st[N][N][2],dx[]={0,0,1,-1},dy[]={1,-1,0,0};
char s[N][N];
struct node {int x,y,u;};
bool check(int x,int y){return x>=1&&y>=1&&x<=h&&y<=w&&s[x][y]=='.';}
int main(){cin>>h>>w>>d>>r;for(int i=1;i<=h;i++)scanf("%s",s[i]+1);//这个写法太妙了！！！一定要会啊memset(st,-1,sizeof(st));st[1][1][0]=0;//初始化queue<node>q;q.push(node{1,1,0});while(!q.empty()&&st[h][w][0]==-1&&st[h][w][1]==-1){//有点跑到终点时候就可以前提停了node cur=q.front();q.pop();for(int i=0;i<4;i++){int x=dx[i]+cur.x,y=dy[i]+cur.y;if(check(x,y)&&st[x][y][cur.u]==-1){q.push((node){x,y,cur.u});//不嗑药的点入队st[x][y][cur.u]=st[cur.x][cur.y][cur.u]+1;//既打标记，又存入答案if(cur.u==0&&check(x+d,y+r)&&st[x+d][y+r][1]==-1){q.push((node){x+d,y+r,1});//嗑药的点入队st[x+d][y+r][1]=st[x][y][0]+1;}}}}if(st[h][w][0]==-1&&st[h][w][1]==-1)cout<<"-1";else{if(st[h][w][0]!=-1&&st[h][w][1]!=-1)cout<<min(st[h][w][0],st[h][w][1]);else {if(st[h][w][0]==-1)cout<<st[h][w][1];else cout<<st[h][w][0];}}
}

看到这里，你果然是高手。