简介

官网

更少训练时间的同时实现最先进的视觉质量，能在1080p分辨率下实现高质量的实时(≥30 fps)新视图合成

NeRF使用隐式场景表示，体素，点云等属于显示建模方法，3DGS就是显示辐射场。它用3D高斯作为灵活高效的表示方法，同时利用神经网络的特性进行参数优化，旨在以更快的训练速度和实时性能实现高质量的渲染，尤其适用于复杂场景和高分辨率输出。

nerf是一个连续的表示，隐含地表示空/占用空间;为了找到空间点的样本，需要进行昂贵的随机抽样，由此产生噪声和计算开销。相比之下，点是一种非结构化的离散表示，它具有足够的灵活性，可以创建、破坏和替换类似于NeRF的几何体。这是通过优化不透明度和位置来实现的，同时避免了完整体积表示的缺点

知识补充

协方差矩阵

方差：度量单个随机变量的离散程度，越大，越离散
$$\begin{array}{r}Var(x)=\frac{1}{n-1}\sum _{i=1}^n(x_i-{\mu }_x{)}^2\end{array}$$
n为样本量，${\mu }_x$表示观测样本的均值

协方差：两个个随机变量的相似程度，负数为负相关，正数为正相关，0为无关
$$\begin{array}{r}Cov(a,b)={\frac{n-1}{\sum }}_{i=1}^n(a_i-{\mu }_a)(b_i-{\mu }_b)\end{array}$$
方差也可以看作是自己对自己求协方差

协方差矩阵
$$\begin{array}{r}\Sigma =\left[\begin{array}{cccc}Cov(x_1,x_1)& Cov(x_1,x_2)& \cdots & Cov(x_1,x_d)\\ Cov(x_2,x_1)& Cov(x_2,x_2)& \cdots & Cov(x_2,x_d)\\ ⋮& ⋮& \ddots & ⋮\\ Cov(x_d,x_1)& Cov(x_d,x_2)& \cdots & Cov(x_d,x_d)\end{array}\right]\in R^{d\times d}\end{array}$$
对角线上的元素为各个随机变量的方差，非对角线上的元素为两两随机变量之间的协方差，协方差矩阵是对称矩阵

球谐函数

如高等数学中的傅里叶变换，任何一个二维函数可以分解为不同的正弦与余弦之和：

$$\begin{array}{r}f(x)=a_0+\sum _{n=1}^{+\infty }{a}_n\cos \frac{n\pi }{i}x+b_n\sin \frac{n\pi }{i}x\end{array}$$

这里的 $\cos \frac{n\pi }{l}x$ 和 $\sin \frac{n\pi }{l}x$叫做基函数，原则上讲当 $n\to +\infty$时，可以完美拟合这个函数，也可以对这个函数进行近似
$$\begin{array}{r}f(x)\approx a_0+\sum _{n=1}^i{a}_n\cos \frac{n\pi }{i}x+b_n\sin \frac{n\pi }{i}x\end{array}$$

如果函数是一个有界的，闭合的，平滑的曲面呢？

可以表示为下述坐标形式

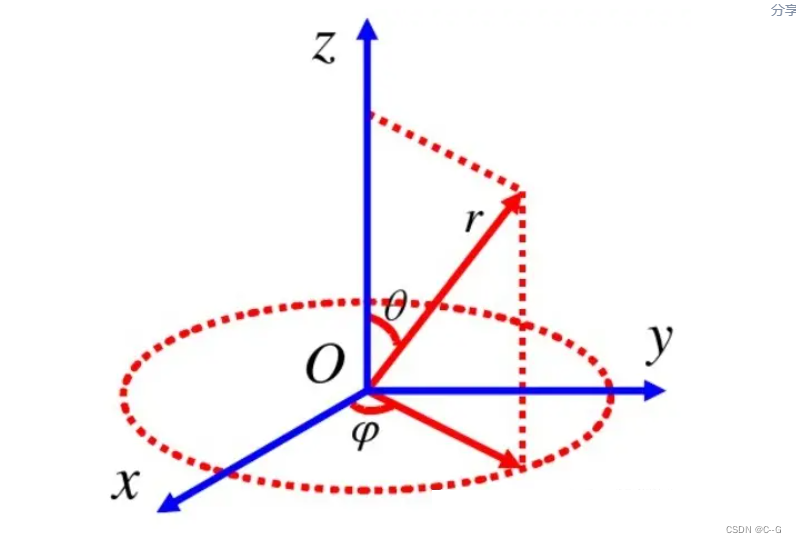
用球面函数表示方法来表示 $f(\theta ,\psi )$，这个函数也有自己基函数组成

球面函数的基函数是

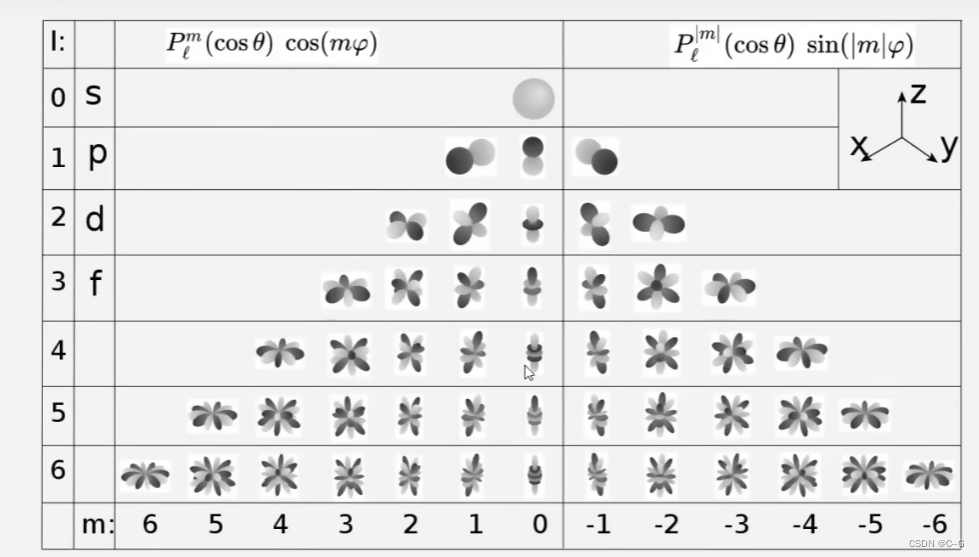
高斯分布

一维高斯分布
$$\begin{array}{r}p(x)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}\end{array}$$
均值为$\mu$，方差为$\sigma$，数据以99%的概率落在$\begin{array}{c}\mu -3\sigma \end{array}$到$\begin{array}{c}\mu +3\sigma \end{array}$之间

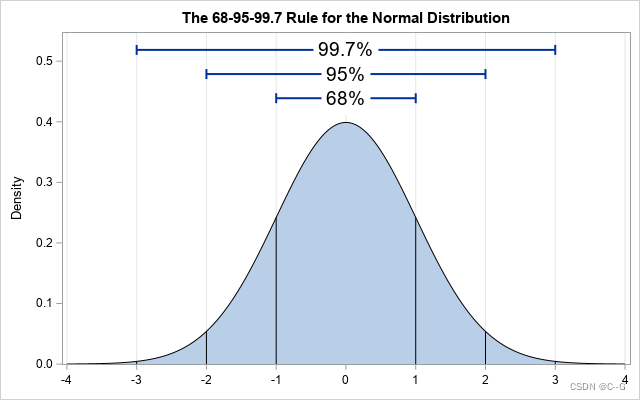
二维标准高斯分布($\mu =0,\sigma =1$)

因为是标准二维高斯分布，所以每个变量之间是独立的
$$\begin{array}{r}p(x,y)=p(x)p(y)=\frac{1}{2\pi }{e}^{(-\frac{x^2+y^2}{2})}\end{array}$$
为了向量化公式，用向量$\begin{array}{c}v=[xy{]}^T\end{array}$表示

$$\begin{array}{r}p(v)=\frac{1}{2\pi }{e}^{-\frac{1}{2}{v}^{T}v}\end{array}$$
这个时候，用$\begin{array}{c}v=A(x-\mu )\end{array}$，其中的 A 为 V 中每个分量的线性组合系数，也就是说 A 表示了每个变量的线性关系
$$\begin{array}{r}p(v)=\frac{|A|}{2\pi }{e}^{-\frac{1}{2}(x-\mu {)}^T{A}^{T}A(x-\mu )}\end{array}$$
用$\begin{array}{c}\Sigma =(A^{T}A{)}^{-1}\end{array}$表示其协方差，其中 |A|为行列式
$$\begin{array}{r}p(v)=\frac{1}{2\pi |\Sigma {|}^{\frac{1}{2}}}{e}^{-\frac{1}{2}(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )}\end{array}$$
图像为

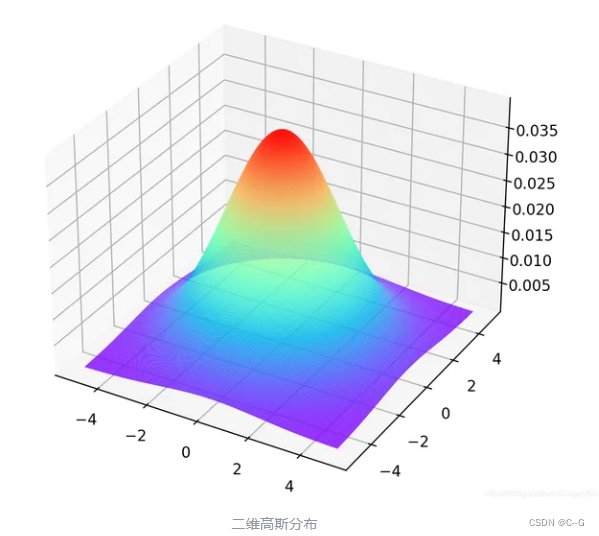
多维高斯分布
$$\begin{array}{r}p(x)=\frac{1}{(2\pi {)}^{\frac{N}{2}}|\Sigma |}{e}^{-\frac{1}{2}(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )}\end{array}$$

假设一个向量 x 服从均值向量为 $\mu$ 、协方差矩阵为 $\Sigma$ 的多元正态分布，令 $\begin{array}{c}\mu =0\end{array}$，由于指数项外面的系统 $\begin{array}{c}\frac{1}{(2\pi {)}^{\frac{N}{2}}|\Sigma |}\end{array}$通常为常数，去掉后简化为：

$$\begin{array}{r}p(x)\propto e^{-\frac{1}{2}(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )}\end{array}$$

三维高斯的图像可以想象一个突起的小山坡

固定概率为 p 的三维高斯分布是什么样呢？

$$\begin{array}{rl}{e}^{-\frac{1}{2}(x-\mu {)}^T{\Sigma }^{-}1(x-\mu )}& =p\\ (x-\mu {)}^T\Sigma (x-\mu )& =-2\ln p\end{array}$$

这里 $-2\ln p$是常数C，$\Sigma$是实对称矩阵，令$\begin{array}{c}\Sigma =P^T\Lambda P\end{array}$

$$\begin{array}{rl}(x-\mu {)}^T{P}^T\Lambda P(x-\mu )& =C\\ (P(x-\mu ){)}^T\Lambda P(x-\mu )& =C\end{array}$$

$y=P(x-\mu )$，令

$$\begin{array}{r}\Lambda =\left[\begin{array}{ccc}{\sigma }_1^2& 0& 0\\ 0& {\sigma }_2^2& 0\\ 0& 0& {\sigma }_3^2\end{array}\right]\end{array}$$

原子式变为
$$C=y^T\Lambda y={\sigma }_1^2{y}_1^2+{\sigma }_2^2{y}_2^2+{\sigma }_3^2{y}_3^2$$

该公式是标准的椭球方程，所以原子式就是把标准椭球经过旋转变换 $P^{-1}$，再挪到 $\mu$点得到。所以对于一个三维高斯而言，同一个椭球表面其概率密度相同，离$\mu$越远，其概率越小。

一个多元高斯轴的长度为$\Sigma$的特征值。
和一维一样，有99%的概率落在$3{\sigma }_1$,$3{\sigma }_2$,$3{\sigma }_3$所在的椭球内，${\sigma }_1,{\sigma }_2,{\sigma }_3$为$\Sigma$的特征值

高斯分布的性质

• 高斯函数的傅里叶变换还是高斯函数
• 高斯函数与高斯函数的卷积仍是高斯函数
• 高斯分布经仿射变换后仍是高斯分布
• 多元高斯分布的边缘分布仍是高斯分布

图形学渲染——坐标变换

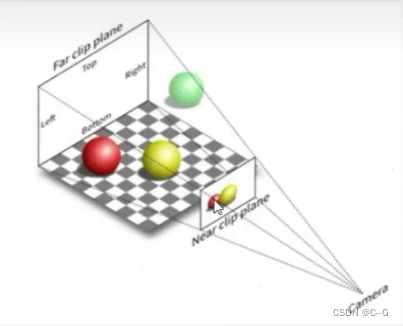
传统图形学的渲染管道里，需要把空间的物体投影到相机平面，也就是需要指导空间每个点到特点相机平面上的位置是多少，传统图形学的流程是：

先把视锥内物体进行一个透视投影，压缩到一个非透视的空间内，然后使用正交投影，将视锥内物体压缩到各维度为[-1,1]的空间内

透视投影就是最类似人眼所看东西的方式，遵循近大远小，如果说正交投影都是水平光线，那么透视投影则显然不是了(左透视，右正交)

透视投影

此时，投影过程可用下图解释，将 (x,y,z)一点投影至投影屏幕之后，他的坐标变为( x′ , y′ , z′ )

图中原点代表视点，z = -n 代表投影平面，利用相似三角形性质不难得出图中投影之后的坐标

那么利用齐次坐标的性质，希望找到一个矩阵完成如下变换

如果形象化的描述一下的话，就是利用这个变换矩阵将整个空间压缩了一下，使其对应了真正透视投影的坐标，最后不要忘了要利用正交转换到$[-1,1{]}^3$的空间之内

首先，这个矩阵的前两行和最后一行是能很快确定出来的，根据最后的齐次坐标，如下：

那么如何确定第三行呢，这里就要运用透视投影的一个性质：

可视空间，前后面变换之后 z 坐标不变





得最后变换矩阵为

正交投影

正交投影是相对简单的一种，坐标的相对位置都不会改变，所有光线都是平行传播，只需将物体（可视部分，即上图的那个长方体）全部转换到一个$[-1,1{]}^3$的空间之中即可（其中x，y坐标便是投影结果，保留z是为了之后的遮挡检测），这只是为了之后的计算更加的方便而已，在转换到屏幕坐标的时候就会重新拉伸回来，所有物体的相对大小位置都不会有任何变化

总的变换公式为

3D Gaussian Splatting

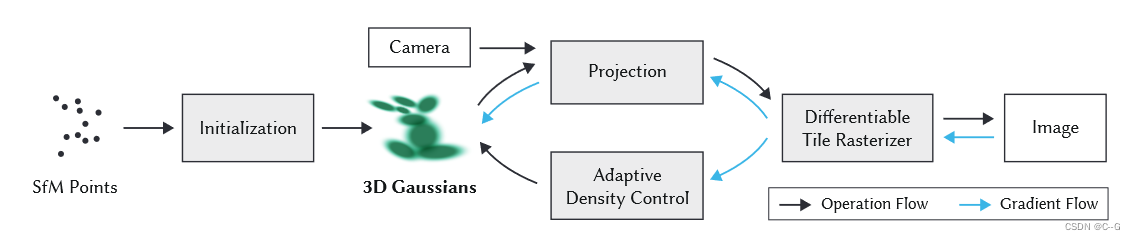
空间点

和particle-based rendering一样，因为点没有体积，所以需要对它进行一个扩展，扩展方式与传统的particle-based rendering 不同，它用3D Gaussian表示

高斯分布由在世界空间中定义的全三维协方差矩阵$\Sigma$定义，以点(mean)为中心

$$\begin{array}{r}G(x)=e^{-\frac{1}{2}(x{)}^T{\Sigma }^{-1}(x)}\end{array}$$

这和前面说的3D Gaussian表示一样，省去了常数项，这种表示具有更强的灵活性，用更少的点表示更复杂的形状

3D 高斯的属性包括：

• 每个点的坐标（中心位置，$\mu$）
• 每个点的高斯表示中的$\Sigma$
• 每个点的颜色
• 每个点的不透明度$\alpha$

$\Sigma$（协方差矩阵）

正定矩阵：
若所有特征值均大于零，则称为正定
A 是 n 阶方阵，如果对任何非零向量 x，都有$x^{T}Ax>0$，$x^T$表示x的转置,则A为正定矩阵。

半正定矩阵：
若所有特征值均不小于零，则称为半正定
A 是 实对称矩阵，如果对任何实非零列向量 x，都有$x^{T}Ax>0$，$x^T$表示x的转置,则A为正定矩阵

这里的$\Sigma$（协方差矩阵）是一个半正定矩阵，要保证这个半正定条件，所以不能对其随机初始化，假定：
$$\begin{array}{rl}\Sigma & =R\Lambda R^T\\ & =R{\Lambda }^{\frac{1}{2}}{\Lambda }^{\frac{1}{2}}{R}^T\\ & =(R{\Lambda }^{\frac{1}{2}})(R{\Lambda }^{\frac{1}{2}}{)}^T\end{array}$$

其中R是一个正交矩阵，可以理解为旋转矩阵，${\Lambda }^{\frac{1}{2}}$是一个全为正数的对角矩阵，可以理解为缩放矩阵，论文的表示为：
$$\begin{array}{r}\Sigma =RS{S}^T{R}^T\end{array}$$

点的颜色 c

为了模拟高光的点，会加入方向向量，使得从不同方向得到不同的颜色，这里使用球谐函数表示。

渲染公式

NeRF体渲染公式

$$\begin{array}{rl}C& =\sum _{i=1}^N{T}_i(1-e^{-{\sigma }_i{\delta }_i})c_{i}with\\ T_i& =e^{-{\sum }_{j=1}^{i-1}{\sigma }_j{\delta }_j}\end{array}$$

同样的这里也使用类似的方式

$$\begin{array}{r}C=\sum _{i\in N}{c}_i{\alpha }_i\prod _{j=1}^{i-1}(1-{\alpha }_i)\end{array}$$

$c_i$是每个点的颜色，${\alpha }_i$是通过对协方差 $\Sigma$乘以每个点不透明度的二维高斯函数进行评估得到

投影（泼溅splatting）

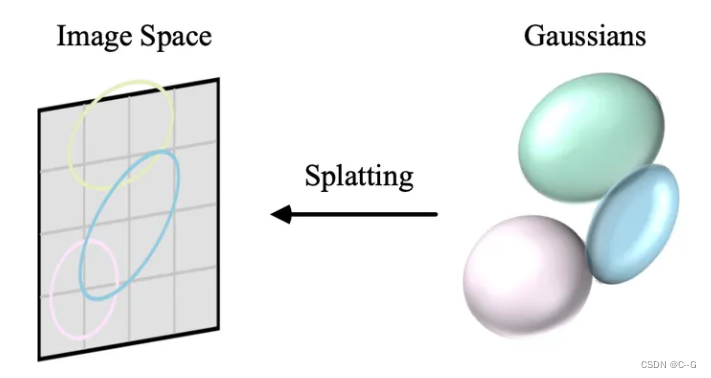
现在，空间点是3D高斯（椭球），携带了中心位置$\mu$、不透明度$\sigma$、3D协方差矩阵$\Sigma$和颜色 c ，渲染方程也如上表述。那么现在就是将3D高斯（椭球）投影到2D图像空间（椭圆）进行渲染。

透视投影
给定视图变化 W ，3D协方差矩阵 $\Sigma$ 从世界坐标转换到相机坐标的公式如下：
$$\begin{array}{r}{\Sigma }_c^{\prime }=W\Sigma W^T\end{array}$$

正交投影
如上述知识补充，我们可以直接用正交投影获得相机平面投影，但是，原始正交头像不考虑z坐标，而渲染公式中需要3D高斯(椭球)的先后顺序（深度），为此，对正交投影进行修改。

假设相机坐标$(t_1,t_2,t_3)$，对其进行压缩到$(x_1,x_2,x_3)$，公式为：
$$\begin{array}{rl}{x}_1& =\frac{t_1}{t_3}\\ x_2& =\frac{t_2}{t_3}\\ x_3& =\sqrt{t_1^2+t_2^2+t_3^2}\end{array}$$

$x_3$的设计是非线性变换，无法通过求解一个变换矩阵求解出来，但是可以用一个线性变换对这个非线性变换进行近似，如泰勒展示式那样：

$$\begin{array}{r}f(x)\approx f(x_0)+f^{\prime }(x_0)(x-x_0)\end{array}$$

$f(x)$的情况就是为 $R\to R$的情况，为了把拓展为高维的 $R^m\to R^n$，使用雅可比矩阵：
$$\begin{array}{r}f(x)\approx f(x_0)+J(x-x_0)\end{array}$$
J是雅可比矩阵，可以看作一阶导的多维形式，假设输入为:$x_1,x_2,\cdots ,x_m$，输出为:$y_1,y_2,\cdots ,y_n$：

$$\begin{array}{r}J=\left[\begin{array}{cccc}\frac{\partial y_1}{x_1}& \frac{\partial y_1}{x_2}& \cdots & \frac{\partial y_1}{x_m}\\ \frac{\partial y_2}{x_1}& \frac{\partial y_2}{x_2}& \cdots & \frac{\partial y_2}{x_m}\\ ⋮& ⋮& \ddots & ⋮\\ \frac{\partial y_n}{x_1}& \frac{\partial y_n}{x_2}& \cdots & \frac{\partial y_n}{x_m}\end{array}\right]\end{array}$$

那么前面的非线性变换可以使用下述公式进行近视，其雅可比矩阵为：
$$\begin{array}{r}\left[\begin{array}{ccc}\frac{1}{t_3}& 0& -\frac{t_1}{t_3}\\ 0& \frac{1}{t_3}& -\frac{t_2}{t_3}\\ \frac{t_1}{\sqrt{t_1^2+t_2^2+t_3^2}}& \frac{t_2}{\sqrt{t_1^2+t_2^2+t_3^2}}& \frac{t_3}{\sqrt{t_1^2+t_2^2+t_3^2}}\end{array}\right]\end{array}$$

对每个高斯在其中心点展开，得到其雅可比矩阵，就可以得到这个高斯的线性变换矩阵。根据高斯分布的性质（高斯分布经仿射变换后仍是高斯分布），如果一个线性变换 $\begin{array}{c}Ax+b\end{array}$，高斯分布经过这个变换之后：

$$\begin{array}{r}{\mu }^{\prime }=A\mu +b\end{array}$$

等同于对线性矩阵$\Sigma$进行下面操作：

$$\begin{array}{r}{\Sigma }^{\prime }=A\Sigma A^T\end{array}$$

给定视图变化W，3D高斯（椭球）从世界坐标到相机坐标再到相机平面的变换公式为：

$$\begin{array}{r}{\Sigma }^{\prime }=JW\Sigma W^T{J}^T\end{array}$$
J为雅可比矩阵，最终就得到了3D高斯投影到相机平面的椭圆

相机平面是2D的，z坐标是用来评估3D高斯先后顺序(深度)的，当丢弃${\Sigma }^{\prime }$的第三行和第三列（z坐标）就是投影到相机平面的协方差矩阵了。

像素点着色

要计算像素点的着色，首先需要知道哪些高斯投影到这个像素点上。投影部分已经知道3D高斯经过仿射变换后投影到平面的高斯，也知道了99%的概率会落在$3{\sigma }_1,3{\sigma }_2$之内，为了简化计算，将范围扩大为$(max(3{\sigma }_1,3{\sigma }_2),max(3{\sigma }_1,3{\sigma }_2))$.

titles(图像块)

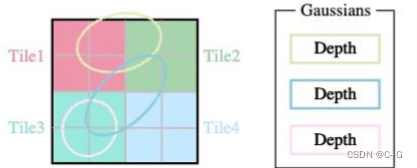
为了避免为每个像素计算有序列表的计算成本，3D GS将精度从像素级别转移到块级别细节。3D GS 将图像划分为多个不重叠的图像块（titles)，每个块包含$16\times 16$像素。进一步确定哪些图像块与投影的高斯（椭圆）相交。

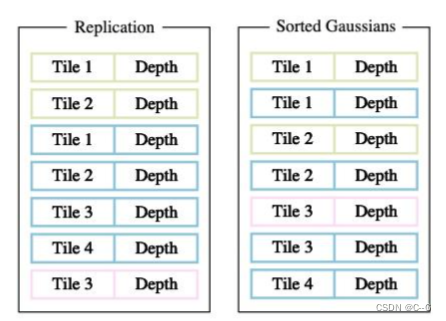
一个投影的高斯可能覆盖多个块，一种合理的方法是复制高斯，为每个副本分配一个标识符（即块ID）

3D GS 会将各自的块 ID 与每个高斯视图变换得到的深度值结合起来。这样就得到了一个未排序的字节列表，其中高位代表块 ID，低位表示深度。这样，使用快速排序后的列表就可以直接用于渲染公式。

每个块和像素的渲染都是独立进行的，因此这一过程非常适合并行计算。另外一个好处是，每个块的像素都可以访问一个公共的共享内存，并保持一个统一的读取序列，从而提高渲染的并行执行效率。在原论文的官方实现中，该框架将块和像素的处理分别视为类似于 CUDA 编程架构中的block和thread。

Adaptive Control

3D GS 是从 structure-from-motion (SfM) 或随机初始化的初始稀疏点集开始的。然后，采用点密集化和剪枝来控制场景中 3D 高斯的密度。

为了稳定，在较低分辨率下“预热”计算。具体来说，使用4倍小的图像分辨率开始优化，并在250次和500次迭代后进行两次上采样。

每100次迭代进行一次密集化，根据当前情况对高斯进行去除或增加

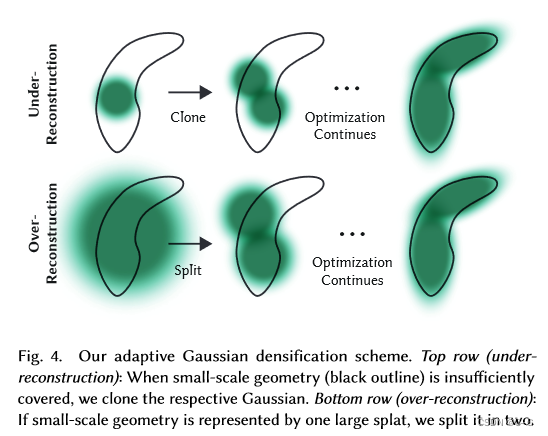
密集化：某些地方的高斯不足。坐标梯度较大（大于阈值 ${\tau }_{pos}$ 0.0002）的地方就表示这里高斯不合适。这涉及到在重建不足的区域克隆小高斯，或者在重建过度的区域拆分大高斯。克隆时，创建一个高斯的副本，并向位置梯度移动。对于分割，则是用两个较小的高斯替换一个较大的高斯，将其比例缩小一个特定的系数。这一步骤旨在优化高斯在三维空间中的分布和表现，从而提高重建的整体质量

剪枝：当透明度非常低 $\alpha$低于某个阈值或者离相机距离非常近（可能是floater）则去掉。这在某种程度上可以看作是一个正则化过程。这样就能有控制地增加必要的高斯密度，同时剔除多余的高斯。这一过程不仅有助于节省计算资源，还能确保模型中的高斯保持精确，从而有效地表现场景。

参数优化

使用sigmoid激活函数将$\alpha$约束在[0−1)范围内并获得平滑梯度，指数激活函数用于协方差的尺度。

3D GS 的损失函数与 NeRF 的略有不同。由于射线步进计算成本高昂，NeRFs通常在像素级别而不是图像级别进行 loss 的计算。

$$\begin{array}{r}\mathcal{L}=(1-\lambda ){\mathcal{L}}_1+\lambda {\mathcal{L}}_{D-SSIM}\end{array}$$

$\lambda =0.2$

SH系数优化对缺乏角度信息很敏感。对于典型的“类似nerf”的捕捉，即通过在其周围的整个半球拍摄的照片来观察中心物体，优化效果很好。然而，如果捕获有角度区域缺失(例如，当捕获场景的角落时，或执行“由内到外”)，则可以通过优化产生SH的零阶分量(即基本色或漫反射色)的完全不正确的值。为了克服这个问题，首先只优化零阶分量，然后在每1000次迭代之后引入SH的一个波段，直到表示所有SH的4个波段。

3D高斯的大多数属性可以通过反向传播直接优化。需要注意的是，直接优化协方差矩阵 $\Sigma$ 可能得到非半正定矩阵，这不符合通常与协方差矩阵相关联的物理解释。为了避免这个问题，3D GS 选择优化一个四元数 q 和一个三维向量 s。q 和 s 分别表示旋转和缩放。这样可以显式的将待优化的参数从9个变为4个。

$$\begin{array}{r}q=q_r+q_i\cdot i+q_j\cdot j+q_k\cdot k\end{array}$$

为了避免自动微分的成本，3D GS 推导了 q 和 s 的梯度，以便在优化过程中直接计算它们。推导过程可参考 3D GS 原论文的附录A