机器学习之决策树现成的模型使用

须知

DecisionTreeClassifier

sklearn.tree.plot_tree

cost_complexity_pruning_path(X_train, y_train)

CART分类树算法

基尼指数

分类树的构建思想

对于离散的数据

对于连续值

剪枝策略

剪枝是什么

剪枝的分类

预剪枝

后剪枝

后剪枝策略体现之威斯康辛州乳腺癌数据集

剪枝策略选用

代码

须知

在代码实现之前，我们先要知道，sklearn里面的tree库中的一些关键模块

DecisionTreeClassifier

sklearn.tree.DecisionTreeClassifier它的作用是创建一个决策树分类器模型

源码：

class sklearn.tree.DecisionTreeClassifier(*, criterion='gini', splitter='best', max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=None, random_state=None, max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None, class_weight=None, presort='deprecated', ccp_alpha=0.0)

我们只需要了解关键参数就好

criterion：这个参数是用来选择使用何种方法度量树的切分质量的，也就是一个选择算法的。

当criterion取值为“gini”时采用基尼不纯度（Gini impurity）算法构造决策树，当criterion取值为 “entropy” 时采用信息增益（ information gain）算法构造决策树，默认为“gini”

splitter：此参数决定了在每个节点上拆分策略的选择。

支持的策略是“best” 选择“最佳拆分策略”， “random” 选择“最佳随机拆分策略”，这个先不做解释，只知道我们默认是“best”就好

max_depth：树的最大深度，取值应当是int类型，如果取值为None,则将所有节点展开，直到所有的叶子都是纯净的或者直到所有叶子都包含少于min_samples_split个样本。

min_samples_split：拆分内部节点所需的最少样本数：
· 如果取值 int , 则将min_samples_split视为最小值。
· 如果为float，则min_samples_split是一个分数，而ceil（min_samples_split * n_samples）是每个拆分的最小样本数。

默认为2
min_samples_leaf：在叶节点（就是我们的树最终的类别）处所需的最小样本数。仅在任何深度的分裂点在左分支和右分支中的每个分支上至少留有min_samples_leaf个训练样本时，才考虑。这可能具有平滑模型的效果，尤其是在回归中。
· 如果为int，则将min_samples_leaf视为最小值
· 如果为float，则min_samples_leaf是一个分数，而ceil（min_samples_leaf * n_samples）是每个节点的最小样本数。
默认为1

ccp_alpha：用于最小化成本复杂性修剪的复杂性参数。将选择在成本复杂度小于ccp_alpha的子树中最大的子树。默认情况下，不执行修剪。有关详细信息，请参见最小成本复杂性修剪。

默认为0.0

了解以上就好了，剩下的可以自行Sklearn 中文社区了解。

sklearn.tree.plot_tree

sklearn.tree.plot_tree(decision_tree, *, max_depth=None, feature_names=None, class_names=None, label='all', filled=False, impurity=True, node_ids=False, proportion=False, rotate='deprecated', rounded=False, precision=3, ax=None, fontsize=None)

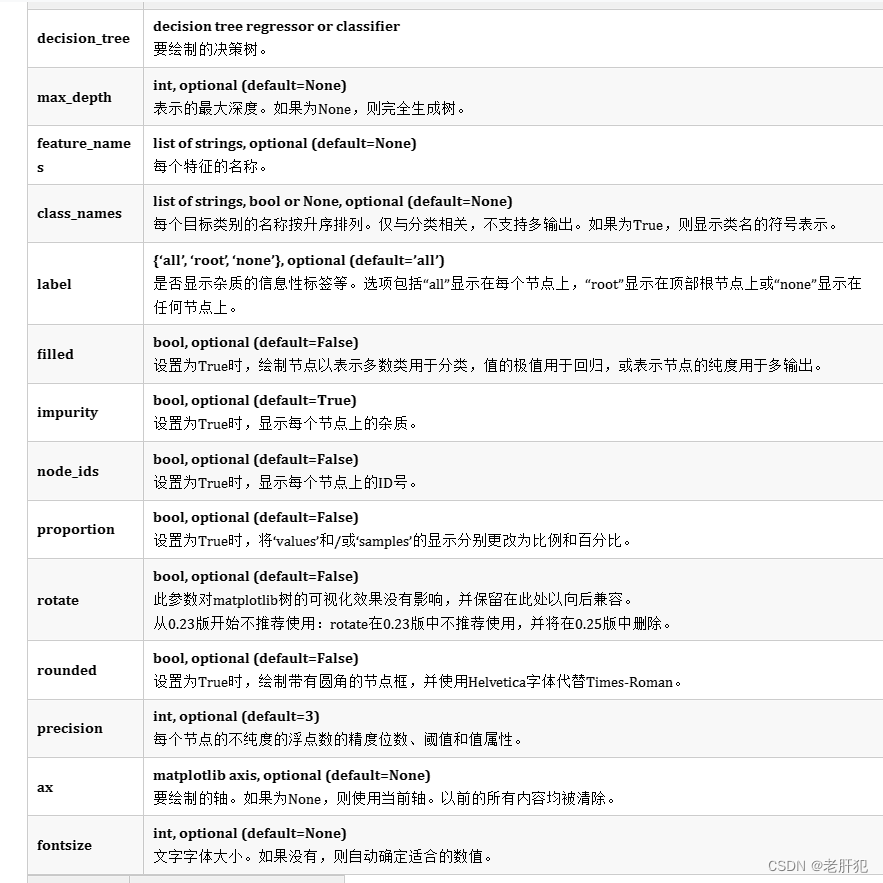（上面图片来自于Sklearn中文社区）

我们只需要记一下常用的就好，比如

feature_names 特征名称的列表，class_names 分类名称的列表（我用列表尝试的是可以的，但是不知道数组或者元组可以不可以，大家可以尝试一下）

另外我们还需要注意：

cost_complexity_pruning_path(X_train, y_train)

他的使用方法如下：

X, y = load_breast_cancer(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)clf = DecisionTreeClassifier(random_state=0)
path = clf.cost_complexity_pruning_path(X_train, y_train)
ccp_alphas, impurities = path.ccp_alphas, path.impurities

官方的解释是：scikit-learn提供了DecisionTreeClassifier.cost_complexity_pruning_path在修剪过程中每一步返回有效的alphas和相应的总叶子不存度。随着alpha的增加，更多的树被修剪，这增加了它的叶子的总不存度。

意思是，cost_complexity_pruning_path(X_train, y_train)是DecisionTreeClassifier(random_state=0)模型里面封装的一个功能模块，我们可以通过这个模型的对象或者说实例化，来调用这个功能，他可以返回在我们这个数据集分类的树，在修剪过程中每一步有效的‘阿尔法’，（没错，alpha就是我们的‘阿尔法’，这是一个参数，用于衡量代价与复杂度之间关系）以及每一步的‘阿尔法’所对应的树的不纯度（用对应不太严谨，应该说每一步最终得到的树的不纯度）。

CART分类树算法

续博客：

决策树算法原理以及ID3、C4.5、CART算法

在上一篇博客中，我们只是提了一下cart分类树的基本算法“基尼算法”，这个算法的核心就是“基尼系数”。

基尼指数

关于基尼系数（基尼指数）：

上面是计算样本的基尼指数。

分类树的构建思想

对于离散的数据

我们一开始选择树的根节点的时候，是把基尼指数最小的特征和该特征的最优切分点给选好的。看“西瓜书”里面的样例。

有些糊但是还可以，我们不需要知道原先的数据集，我们只是看一下，找根节点的思想就好了

就是把每个特征的最小的基尼指数的特征值拉出来，然后比较他们的基尼指数找到最小的特征值，那么这个特征值所属的特征就是根节点，而该特征值就是划分点。

分好根节点之后，我们根据划分点，把是该特征值的分为一类，作为叶子节点。（在叶子节点中，哪个种类的样本多，该叶子节点就是哪一类）

其他的分为另一类，然后接着按照之前的步骤接着分，循环往复，最后得到的其实是一个二叉树。

对于连续值

有的时候我们的特征值是连续的数据，就比如特征“金钱数额”，它对应的特征值是一个个的数值，所以这时候就需要其他的处理方法。（截图内容来自知乎）

简而言之，就是把连续转化为离散，然后其他的就和离散的数据的处理方法一样，最后的到一个二叉树。

剪枝策略

剪枝是什么

剪枝顾名思义就是减去树的多余的“枝叶”，在我们的决策树里体现为，把一些子节点的叶节点去掉，让子节点成为叶节点

剪枝的分类

剪枝主要分为，预剪枝，后剪枝。

后剪枝的方法很多，现在说一些我们常用的：错误率降低剪枝REP（Reduced-Error Pruning）、悲观错误剪枝PEP（Pesimistic-Error Pruning）、代价复杂度剪枝CCP（Cost Complexity Pruning）、最小错误剪枝MEP。

预剪枝

预剪枝就是在我们构建树的每个节点前，都要计算样本的准确度有没有提升，没有提升我们就不构建，换一个划分点，提升了就接着划分。

具体原理推荐大家看一下这位网友在知乎的这篇博客：决策树总结（三）剪枝

（我们主要分析后剪枝）

预剪枝实例思路：先用默认值，让树完整生长，再参考完全生长的决策树的信息，分析树有没有容易过拟合的表现，通过相关参数，对过分生长的节点作出限制，以新参数重新训练决策树。

的确，并没有体现出预剪枝的思想，但是没办法，这个方法其实我们真不常用，现成的模型中基本都是后剪枝。

后剪枝

代价复杂度剪枝CCP：同CART剪枝算法(最常用)。

错误率降低剪枝REP：划分训练集-验证集。训练集用于形成决策树；验证集用来评估修剪决策树。大致流程可描述为：对于训练集上构建的过拟合决策树，自底向上遍历所有子树进行剪枝，直到针对交叉验证数据集无法进一步降低错误率为止。

悲观错误剪枝PEP：悲观错误剪枝也是根据剪枝前后的错误率来决定是否剪枝，和REP不同的是，PEP不需要使用验证样本，并且PEP是自上而下剪枝的。

最小错误剪枝MEP：MEP 希望通过剪枝得到一棵相对于独立数据集来说具有最小期望错误率的决策树。所使用的独立数据集是用来简化对未知样本的错分样本率的估计的,并不意味真正使用了独立的剪枝集 ,实际情况是无论早期版本还是改进版本均只利用了训练集的信息。

CCP算法：为子树Tt定义了代价和复杂度，以及一个衡量代价与复杂度之间关系的参数a。其中代价指的是在剪枝过程中因子树T_t被叶节点替代而增加的错分样本；复杂度表示剪枝后子树Tt减少的叶结点数；a则表示剪枝后树的复杂度降低程度与代价间的关系。在树构建完成后，对树进行剪枝简化，使以下损失函数最小化：损失函数既考虑了代价，又考虑了树的复杂度，所以叫代价复杂度剪枝法，实质就是在树的复杂度与准确性之间取得一个平衡点。备注：在sklearn中，如果criterion设为gini，Li 则是每个叶子节点的gini系数，如果设为entropy，则是熵。

后剪枝策略体现之威斯康辛州乳腺癌数据集

剪枝策略选用

CCP算法

代码

from matplotlib import font_manager
from sklearn import datasets  # 导入数据集
from sklearn import tree
from sklearn.model_selection import \train_test_split  # 导入数据分离包 用法：X_train,X_test, y_train, y_test = train_test_split(train_data, train_target, test_size, random_state, shuffle)
import numpy
import matplotlib.pyplot as pltdata = datasets.load_breast_cancer()
#print(data)
#key=data.keys()
#print(key) #dict_keys(['data', 'target', 'frame', 'target_names', 'DESCR', 'feature_names', 'filename', 'data_module'])
sample=data['data']
#print(sample)
#print(sample.shape)#(569, 30) 一共569行 每行数据都有30个特征
#print(data['target'])
target=data['target']
#print(target)
# [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
#  1 0 0 0 0 0 0 0 0 1 0 1 1 1 1 1 0 0 1 0 0 1 1 1 1 0 1 0 0 1 1 1 1 0 1 0 0
#  1 0 1 0 0 1 1 1 0 0 1 0 0 0 1 1 1 0 1 1 0 0 1 1 1 0 0 1 1 1 1 0 1 1 0 1 1
#  1 1 1 1 1 1 0 0 0 1 0 0 1 1 1 0 0 1 0 1 0 0 1 0 0 1 1 0 1 1 0 1 1 1 1 0 1
#  1 1 1 1 1 1 1 1 0 1 1 1 1 0 0 1 0 1 1 0 0 1 1 0 0 1 1 1 1 0 1 1 0 0 0 1 0
#  1 0 1 1 1 0 1 1 0 0 1 0 0 0 0 1 0 0 0 1 0 1 0 1 1 0 1 0 0 0 0 1 1 0 0 1 1
#  1 0 1 1 1 1 1 0 0 1 1 0 1 1 0 0 1 0 1 1 1 1 0 1 1 1 1 1 0 1 0 0 0 0 0 0 0
#  0 0 0 0 0 0 0 1 1 1 1 1 1 0 1 0 1 1 0 1 1 0 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1
#  1 0 1 1 0 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 0 1 0 1 1 1 1 0 0 0 1 1
#  1 1 0 1 0 1 0 1 1 1 0 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1 1 1 1 1 1 1 0 0 1 0 0
#  0 1 0 0 1 1 1 1 1 0 1 1 1 1 1 0 1 1 1 0 1 1 0 0 1 1 1 1 1 1 0 1 1 1 1 1 1
#  1 0 1 1 1 1 1 0 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 0 1 0 0 1 0 1 1 1 1 1 0 1 1
#  0 1 0 1 1 0 1 0 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 0 1
#  1 1 1 1 1 1 0 1 0 1 1 0 1 1 1 1 1 0 0 1 0 1 0 1 1 1 1 1 0 1 1 0 1 0 1 0 0
#  1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 0 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
#  1 1 1 1 1 1 1 0 0 0 0 0 0 1]
#print(data['target_names'])#['malignant' 'benign']三种类型分别对应：0，1#b=[0.05,0.1,0.15,0.2,0.25,0.3,0.35,0.4,0.45,0.5,0.55,0.6,0.75]
#b = [0.05,0.06,0.07,0.08, 0.1,0.11,0.12,0.13,0.14, 0.15,0.16,0.17,0.18,0.19,0.2, 0.21, 0.22,0.25,0.27,0.29 ,0.3,0.33, 0.35,0.37, 0.4,0.45,0.5]
# b = [0.01,0.02,0.03,0.05,0.06,0.07,0.08,0.09, 0.1]
# a = []
# for x in b:
#     train_data,test_data,train_target,test_target=train_test_split(sample,target,test_size=x,random_state=2020)
#     tree_= tree.DecisionTreeClassifier()
#     tree_.fit(train_data,train_target)
#     print('模型的准确度:',tree_.score(test_data,test_target))
#     a.append(tree_.score(test_data,test_target))
# plt.plot(b,a)
# plt.show()
#测试集尺寸选择0.03比较合适
#开始创建模型
train_data, test_data, train_target, test_target = train_test_split(sample, target, test_size=0.03, random_state=2020)
tree_ = tree.DecisionTreeClassifier()
tree_.fit(train_data, train_target)
print('模型准确度：',tree_.score(test_data, test_target))
tree.plot_tree(tree_,filled=True,feature_names=data['feature_names'],class_names=data['target_names'])
plt.show()
print('在叶子节点对应的索引---------------------')
print(tree_.apply(sample))
print( '预测-----------------------')
# [1.799e+01 1.038e+01 1.228e+02 1.001e+03 1.184e-01 2.776e-01 3.001e-01
#  1.471e-01 2.419e-01 7.871e-02 1.095e+00 9.053e-01 8.589e+00 1.534e+02
#  6.399e-03 4.904e-02 5.373e-02 1.587e-02 3.003e-02 6.193e-03 2.538e+01
#  1.733e+01 1.846e+02 2.019e+03 1.622e-01 6.656e-01 7.119e-01 2.654e-01
#  4.601e-01 1.189e-01],0
b = [sample[0]]
b_target = tree_.predict(b)
print(b_target)
# # 优化：
# #优化方式一：从整个树开始处理一些枝节
print('从整个树开始处理一些枝节--------------------------------')
tree_ = tree.DecisionTreeClassifier(min_samples_leaf=15,random_state=0)
tree_.fit(train_data, train_target)
tree.plot_tree(tree_,filled=True,feature_names=data['feature_names'],class_names=data['target_names'])
plt.show()
print('模型准确度：',tree_.score(test_data, test_target))
print('在叶子节点对应的索引---------------------')
print(tree_.apply(sample))
# print( '预测-----------------------')
# [1.799e+01 1.038e+01 1.228e+02 1.001e+03 1.184e-01 2.776e-01 3.001e-01
#  1.471e-01 2.419e-01 7.871e-02 1.095e+00 9.053e-01 8.589e+00 1.534e+02
#  6.399e-03 4.904e-02 5.373e-02 1.587e-02 3.003e-02 6.193e-03 2.538e+01
#  1.733e+01 1.846e+02 2.019e+03 1.622e-01 6.656e-01 7.119e-01 2.654e-01
#  4.601e-01 1.189e-01],0
b = [sample[0]]
b_target = tree_.predict(b)
print(b_target)
# #优化方式二：后剪枝cpp
print('后剪枝cpp------------------')
tree_ = tree.DecisionTreeClassifier(min_samples_leaf=15,random_state=0)
tree_.fit(train_data, train_target)
impuritiesandalphas=tree_.cost_complexity_pruning_path(train_data,train_target)
impurities=impuritiesandalphas.impurities
alphas=impuritiesandalphas.ccp_alphas
print('impurities',impurities)
print('alphas',alphas)
print('开始后剪枝训练------------------')
# test_=[0.       ,  0.00046032 ,0.000881  , 0.00194334, 0.01499473, 0.0181062,0.04895626 ,0.32369286]
# test_=[0.       ,  0.00046032 ,0.000881  , 0.00194334, 0.01499473, 0.0181062,0.04895626]
# test_=[0.       ,  0.00046032 ,0.000881  , 0.00194334, 0.01499473, 0.0181062,0.02]
# scor_=[]
# for x in test_:
#     tree_ = tree.DecisionTreeClassifier(min_samples_leaf=5,random_state=0,ccp_alpha=x)
#     tree_.fit(train_data, train_target)
#     print('模型准确度：',tree_.score(test_data, test_target))
#     scor_.append(tree_.score(test_data, test_target))
# font = font_manager.FontProperties(fname="C:\\Users\\ASUS\\Desktop\\Fonts\\STZHONGS.TTF")
# plt.plot(test_, scor_, "r", label='模型精准度')
# plt.title('参数alpha和模型精准度的关系', fontproperties=font, fontsize=18)
# plt.legend(prop=font)
# plt.show()
#alpha=0.02
al=0.02
tree_ = tree.DecisionTreeClassifier(min_samples_leaf=15,random_state=0,ccp_alpha=al)
tree_.fit(train_data, train_target)
tree.plot_tree(tree_,filled=True,feature_names=data['feature_names'],class_names=data['target_names'])
plt.show()
print('模型准确度：',tree_.score(test_data, test_target))
print('在叶子节点对应的索引---------------------')
print(tree_.apply(sample))
print(f'alpha={al}时树的纯度：')
is_leaf =tree_.tree_.children_left ==-1
tree_impurities = (tree_.tree_.impurity[is_leaf]* tree_.tree_.n_node_samples[is_leaf]/len(train_target)).sum()
print(tree_impurities)
print( '预测-----------------------')
# [1.799e+01 1.038e+01 1.228e+02 1.001e+03 1.184e-01 2.776e-01 3.001e-01
#  1.471e-01 2.419e-01 7.871e-02 1.095e+00 9.053e-01 8.589e+00 1.534e+02
#  6.399e-03 4.904e-02 5.373e-02 1.587e-02 3.003e-02 6.193e-03 2.538e+01
#  1.733e+01 1.846e+02 2.019e+03 1.622e-01 6.656e-01 7.119e-01 2.654e-01
#  4.601e-01 1.189e-01],0
b = [sample[0]]
b_target = tree_.predict(b)
print(b_target)

总之我们要根据模型生成的树来进行剪枝判断，从而更改模型参数。