这题没做出来，查了一些博客，下面是我比较能接受的理解和书写方式。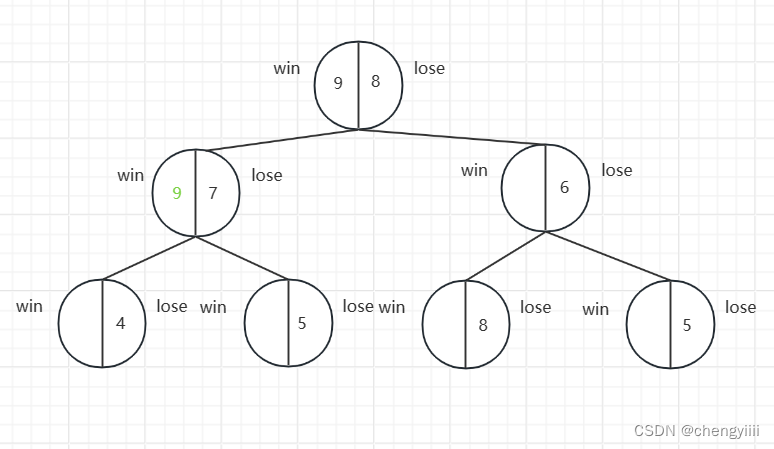

读完题可以发现这是一个满二叉树，并且可以得到每场比赛失败者的信息（决赛是胜利者和失败者都可以得到）
对于一场比赛，它的胜利者要么是左孩子中的胜利者，要么是右孩子中的胜利者，那我们就可以先假设是左孩子的胜利者，如果不行就交换（是右孩子的胜利者），如果都不无法满足
条件，说明根本无解。
也就是说这个9可能是左边这个结点的win,也可能是右边的win,只要有一次试探成功就能返回true。

写代码：

#include <bits/stdc++.h>
using namespace std;
const int N = 1 << 20;
struct node {int win;int lose;
}tree[N];
bool dfs(int n,int ssize) {if (n > ssize) return true;if (tree[n].win < tree[n].lose) {return false;}tree[2 * n].win = tree[n].win;//做出假设tree[2 * n + 1].win = tree[n].lose;if (dfs(2 * n, ssize) && dfs(2 * n + 1, ssize)) {return true;}swap(tree[2 * n].win, tree[2 * n + 1].win);if (dfs(2 * n, ssize) && dfs(2 * n + 1, ssize)) {return true;}return false;
}
int main() {int k;//层数cin >> k;for (int i = k; i >= 1; i--) {for (int j = 1 << (i - 1); j < 1 << i; j++) {cin >> tree[j].lose;}}//输入最后一轮的赢者cin >> tree[1].win;int ssize = (1 << k) - 1;int flag = 0;if (dfs(1,ssize)) {for (int j = 1 << (k - 1); j < 1 << k; j++) {if (flag == 0) {cout << tree[j].win << " " << tree[j].lose;flag = 1;}else {cout << " " << tree[j].win << " " << tree[j].lose;}}}else {cout << "No Solution" << '\n';}return 0;
}