算法学习——LeetCode力扣动态规划篇2

343. 整数拆分
343. 整数拆分 - 力扣(LeetCode)
描述
给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k >= 2 ),并使这些整数的乘积最大化。
返回 你可以获得的最大乘积 。
示例
示例 1:
输入: n = 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。
示例 2:
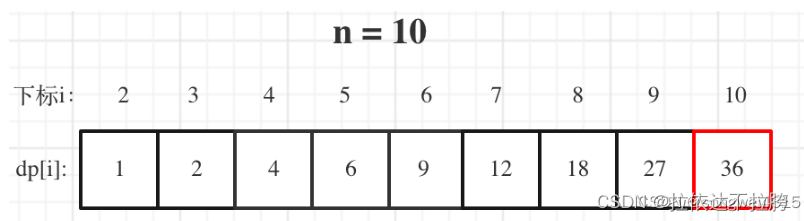
输入: n = 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
提示
2 <= n <= 58
代码解析
dp[i]:分拆数字i,可以得到的最大乘积为dp[i]。
确定递推公式
可以想 dp[i]最大乘积是怎么得到的呢?
其实可以从1遍历j,然后有两种渠道得到dp[i].
一个是j * (i - j) 直接相乘。
一个是j * dp[i - j],相当于是拆分(i - j),对这个拆分不理解的话,可以回想dp数组的定义。
也可以这么理解,j * (i - j) 是单纯的把整数拆分为两个数相乘,而j * dp[i - j]是拆分成两个以及两个以上的个数相乘。
所以递推公式:dp[i] = max({dp[i], (i - j) * j, dp[i - j] * j});
那么在取最大值的时候,为什么还要比较dp[i]呢?
因为在递推公式推导的过程中,每次计算dp[i],取最大的而已。
class Solution {
public:int integerBreak(int n) {vector<int> dp(n+1,0);dp[2] = 1 ; for(int i=3 ; i<=n;i++){//计算i的分割点,j从1开始分割到i-1for(int j=1 ; j<i ;j++){//找到最大乘积的时候dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));cout<<"i:"<<i<<" dp:"<<dp[i]<<endl;}}return dp[n];}
};96. 不同的二叉搜索树
96. 不同的二叉搜索树 - 力扣(LeetCode)
描述
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
示例
示例 1:
输入:n = 3
输出:5
示例 2:
输入:n = 1
输出:1
提示
1 <= n <= 19
代码描述
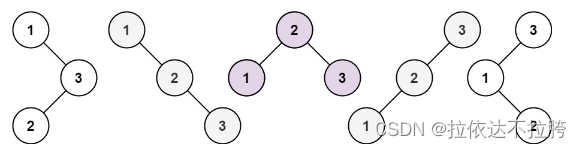
当3为头结点的时候,其左子树有两个节点,看这两个节点的布局,是不是和n为2的时候两棵树的布局也是一样的啊!
当2为头结点的时候,其左右子树都只有一个节点,布局是不是和n为1的时候只有一棵树的布局也是一样的啊!
dp[3],就是 元素1为头结点搜索树的数量 + 元素2为头结点搜索树的数量 + 元素3为头结点搜索树的数量
元素1为头结点搜索树的数量 = 右子树有2个元素的搜索树数量 * 左子树有0个元素的搜索树数量
元素2为头结点搜索树的数量 = 右子树有1个元素的搜索树数量 * 左子树有1个元素的搜索树数量
元素3为头结点搜索树的数量 = 右子树有0个元素的搜索树数量 * 左子树有2个元素的搜索树数量
所以dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2]
动态规划
确定递推公式
dp[i] += dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量]
j相当于是头结点的元素,从1遍历到i为止。
所以递推公式:dp[i] += dp[j - 1] * dp[i - j];
j-1 为j为头结点左子树节点数量,i-j 为以j为头结点右子树节点数量
dp数组如何初始化
从定义上来讲,空节点也是一棵二叉树,也是一棵二叉搜索树,这是可以说得通的。
j为头结点左子树节点数量为0,也需要dp[以j为头结点左子树节点数量] = 1, 否则乘法的结果就都变成0了。
所以初始化dp[0] = 1
class Solution {
public:int numTrees(int n) {if(n<=2) return n;vector<int> dp(n+1,0);dp[0] = 1;dp[1] = 1;dp[2] = 2;for(int i=3 ; i<=n ;i++){for(int j=1 ; j<=i ;j++){dp[i] += dp[j-1] * dp[i-j];}}return dp[n];}
};416. 分割等和子集
416. 分割等和子集 - 力扣(LeetCode)
描述
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
示例
示例 1:
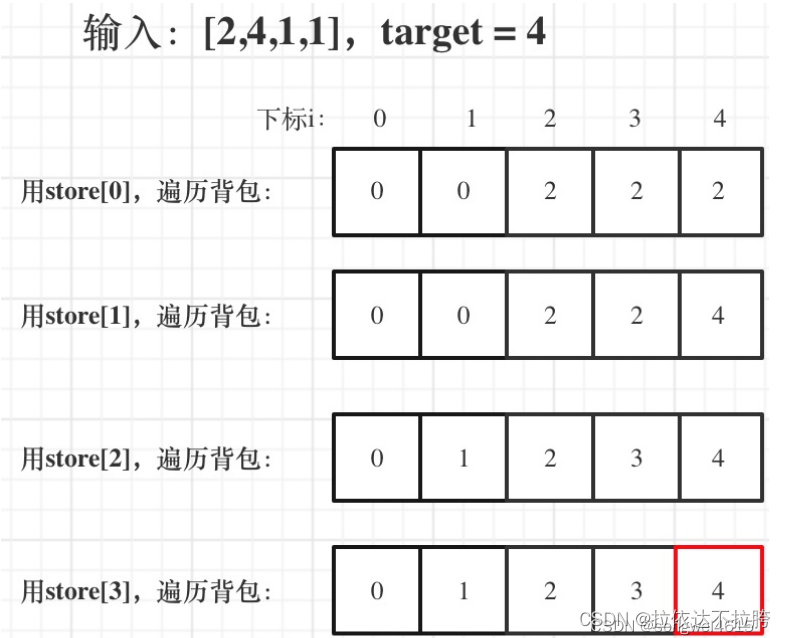
输入:nums = [1,5,11,5]
输出:true
解释:数组可以分割成 [1, 5, 5] 和 [11] 。
示例 2:
输入:nums = [1,2,3,5]
输出:false
解释:数组不能分割成两个元素和相等的子集。
提示
1 <= nums.length <= 200
1 <= nums[i] <= 100
代码解析
一个商品如果可以重复多次放入是完全背包,而只能放入一次是01背包,写法还是不一样的。
本题中使用的是01背包,因为元素我们只能用一次。
- 背包的体积为sum / 2
- 背包要放入的商品(集合里的元素)重量为元素的数值,价值也为元素的数值
- 背包如果正好装满,说明找到了总和为 sum / 2 的子集。
- 背包中每一个元素是不可重复放入。
动态背包(二维背包)
dp[ i ][ j ] 中
- i 是放入背包中元素的范围,从0 - i 中取元素,每个元素取一次。
- j 是当前背包的容量上限
本题的核心是找到刚好背包容量是sum/2装满的时候。
class Solution {
public:bool canPartition(vector<int>& nums) {int sum = 0 , target = 0;for(auto it:nums) sum += it;//如果和是奇数,就不能分成两个相等的子集if(sum%2 == 1) return false; //目标是找到sum/2target = sum/2;vector<vector<int>> dp(nums.size() , vector<int>(target+1 , 0));//背包初始化第一行的值,第一行是只能放第一个元素//检查背包的大小能否放进去,能就放进去第一个元素,不能就空着//第一列是背包容量是0的时候,dp[i][0]也都是0,不用额外初始化for(int j = 1 ; j<=target ;j++ )if(j>=nums[0]) dp[0][j] = nums[0];//开始遍历for(int i=1 ; i<nums.size() ;i++){for(int j = 1 ; j<=target ;j++){//如果当前值大于背包的容量,就不放进去if(j < nums[i]) dp[i][j] = dp[i-1][j];//如果可以放进去,就找放进去和不放进去大的一个else dp[i][j] = max(dp[i-1][j],dp[i-1][j-nums[i]] + nums[i]);}}//最后在背包大小是sum/2的一列里找,刚好背包装满的for(int i=0; i<nums.size();i++)if(dp[i][target]==target) return true;return false;}
};1049. 最后一块石头的重量 II
1049. 最后一块石头的重量 II - 力扣(LeetCode)
描述
有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。
每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x <= y。那么粉碎的可能结果如下:
如果 x == y,那么两块石头都会被完全粉碎;
如果 x != y,那么重量为 x 的石头将会完全粉碎,而重量为 y 的石头新重量为 y-x。
最后,最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下,就返回 0。
示例
示例 1:
输入:stones = [2,7,4,1,8,1]
输出:1
解释:
组合 2 和 4,得到 2,所以数组转化为 [2,7,1,8,1],
组合 7 和 8,得到 1,所以数组转化为 [2,1,1,1],
组合 2 和 1,得到 1,所以数组转化为 [1,1,1],
组合 1 和 1,得到 0,所以数组转化为 [1],这就是最优值。
示例 2:
输入:stones = [31,26,33,21,40]
输出:5
提示
1 <= stones.length <= 30
1 <= stones[i] <= 100
代码解析
本题其实就是尽量让石头分成重量相同的两堆,相撞之后剩下的石头最小,这样就化解成01背包问题了。
本题物品的重量为store[i],物品的价值也为store[i]。
动态规划(二维数组)
找到总重量最接近sum/2 的背包,这是一个石头堆。
和另一个堆相减,就是剩下的
class Solution {
public:int lastStoneWeightII(vector<int>& stones) {if(stones.size() == 1 ) return stones[0];int sum = 0;for(auto it:stones) sum += it;vector<vector<int>> dp (stones.size() , vector<int>( sum /2 + 1 , 0) ) ;for(int j=1 ; j<=sum/2 ;j++)if(j>=stones[0]) dp[0][j] = stones[0];//找到背包为sum/2以内最大的种类for(int i=1 ;i<stones.size() ;i++){for(int j=1 ; j<=sum/2 ;j++){if(j>=stones[i]) dp[i][j] = max( dp[i-1][j] , dp[i-1][j-stones[i]] + stones[i]);else dp[i][j] = dp[i-1][j];}}//找到最接近sum/2的背包int bag_max = 0;for(int i=0 ;i<stones.size() ;i++ ){if(dp[i][sum/2] > bag_max) bag_max = dp[i][sum/2];}//计算石头堆的差return (sum - bag_max) - bag_max;}
};动态规划(滚动数组)
class Solution {
public:int lastStoneWeightII(vector<int>& stones) {if(stones.size() == 1 ) return stones[0];int sum = 0;for(auto it:stones) sum += it;vector<int> dp (sum /2 + 1 , 0);for(int i=0 ;i<stones.size() ;i++){for(int j=sum/2 ; j>=0 ;j--){if(j>=stones[i]) dp[j] = max( dp[j] , dp[j-stones[i]] + stones[i]);else dp[j] = dp[j];}}return (sum - dp[sum/2]) - dp[sum/2];}
};