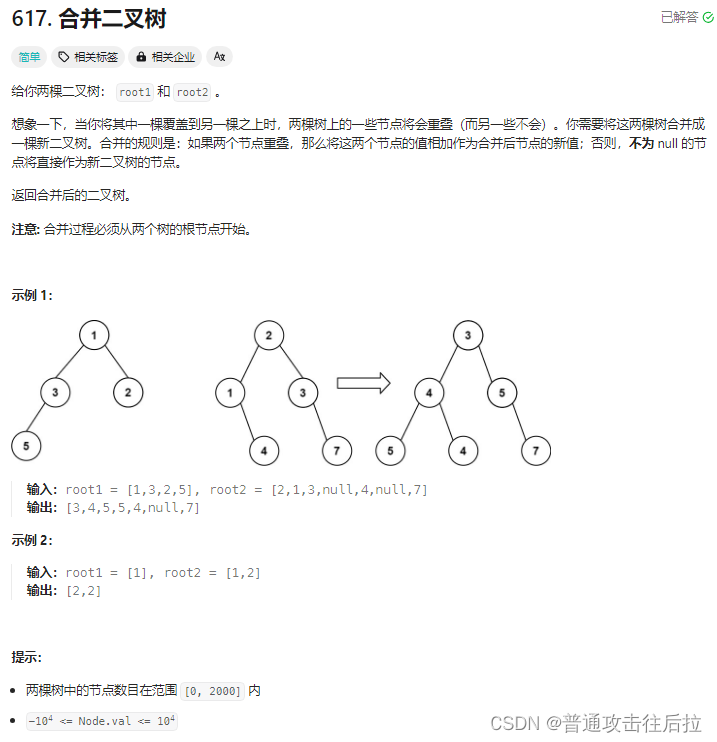
心路历程:
看到两颗二叉树的问题,第一反应想到了同频遍历,然后每一步创建新的结点,虽然也写出来了但是代码比较长,而且空间复杂度比较高,好处是没有修改原始的两个二叉树的结果。
后来看了网上的解答,发现可以直接按照修改其中一个二叉树来做,这样代码量会少很多,并且空间复杂度会低,但是这样会导致原来的二叉树被修改。
注意的点:
1、每当调用node.left时都需要保证node不是None
2、当想不明白应该在循环哪一步新建变量时,可以按照循环不变量的角度去思考
3、递归函数return值时,边界return,非边界也要return,是统一的
解法一:同频遍历+创建新的二叉树
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def mergeTrees(self, root1: Optional[TreeNode], root2: Optional[TreeNode]) -> Optional[TreeNode]:if not root1 and not root2:return Nonenew_root = TreeNode()# 二叉树同频深度遍历def dfs(node1, node2, new_node):if not node1 and not node2: returnif node1 and not node2:new_node.val = node1.valelif not node1 and node2: new_node.val = node2.valelse:new_node.val = node1.val + node2.valif (node1 and node1.left) or (node2 and node2.left):new_node_left = TreeNode()new_node.left = new_node_leftif node1 and node2:dfs(node1.left, node2.left, new_node.left)elif node1 and not node2:dfs(node1.left, None, new_node.left)elif not node1 and node2:dfs(None, node2.left, new_node.left)if (node1 and node1.right) or (node2 and node2.right):new_node_right = TreeNode()new_node.right = new_node_rightif node1 and node2:dfs(node1.right, node2.right, new_node.right)elif node1 and not node2:dfs(node1.right, None, new_node.right)elif not node1 and node2:dfs(None, node2.right, new_node.right)dfs(root1, root2, new_root)return new_root
解法二:修改其中一颗二叉树,递归函数直接返回合并后的一个结点
def mergeTrees(self, root1: Optional[TreeNode], root2: Optional[TreeNode]) -> Optional[TreeNode]:def dfs(node1, node2): # 将node2结点合并到node1,返回合并后的node1结点if not node1: return node2if not node2: return node1node1.val += node2.valnode1.left = dfs(node1.left, node2.left)node1.right = dfs(node1.right, node2.right)return node1return dfs(root1, root2)