背景
首先带大家了解一下汉诺塔问题
汉诺塔是一个典型的函数递归问题,汉诺塔描述了这样的场景,有三个柱子,A,B,C,A柱为起始柱,在A柱上面有若干大小不同的盘子,最下面的最大,最上面的最小,从下往上依次递减,我们将通过一些方式将这些盘子移动到C柱上,在移动的过程中,我们可以借助B柱,也就是辅助我们完成A->C柱的移动。在移动盘子的时候有些规则需要我们遵守。
1.每次只能移动一个盘子。
2.大盘子永远不能放在小盘子上面。

递归的概念
什么是递归?
程序调用自身的编程技巧称为递归,递归作为一种算法在程序设计中广泛应用。一个过程或者函数在其他定义或说明中有直接或间接调用自身的一种方法被称之为递归。
递归通常把一个大的复杂的问题层层转化成一个与原问题相似的规模较小的问题来求解。
递归算法只需要少量的程序就可以描述出解题过程所需要的多次重复计算,大大减少了程序的代码量。
但是想要使用递归有两个必要的条件
1.递归必须存在限制条件,当满足这个限制条件的时候,递归不再继续。
2.每次的递归调用之后会越来越接近这个限制条件。
在我们今天的汉诺塔问题中,限制条件就是n=1
汉诺塔问题图解
我们来简单模拟一下三个盘子的移动,体会一下汉诺塔问题。
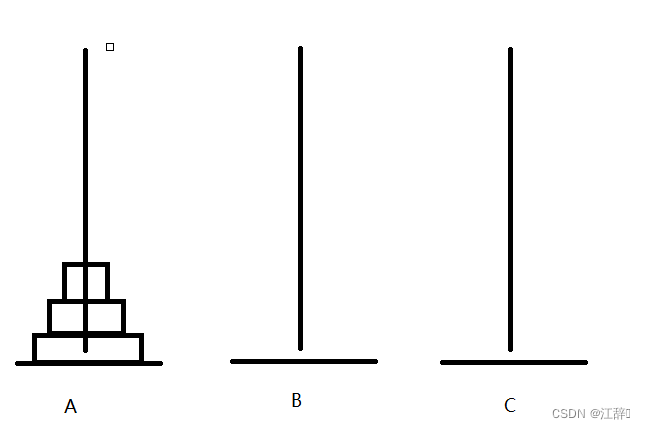
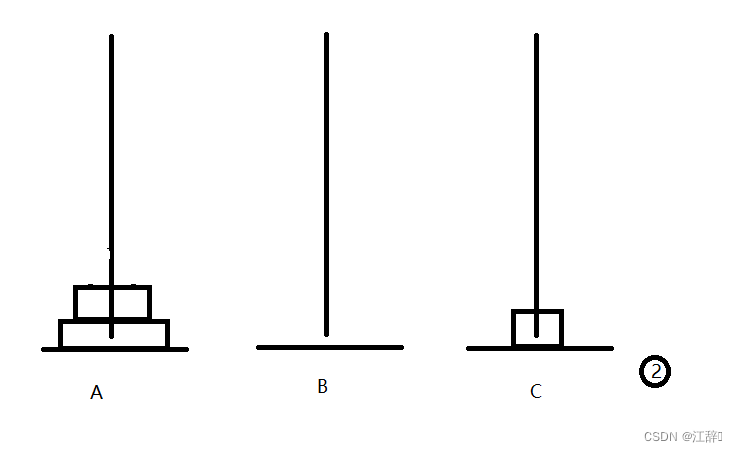

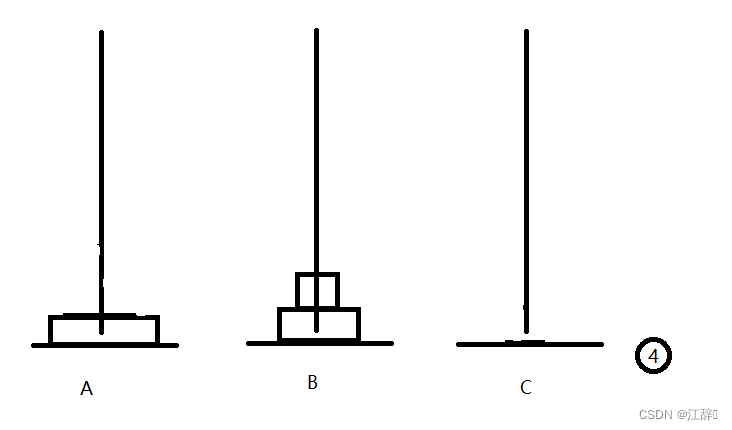
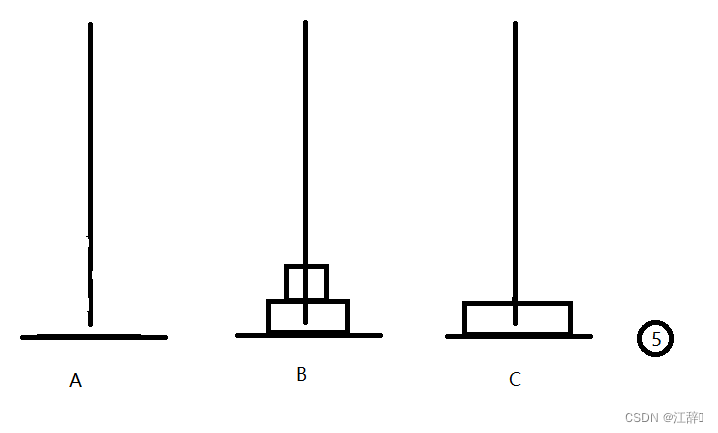
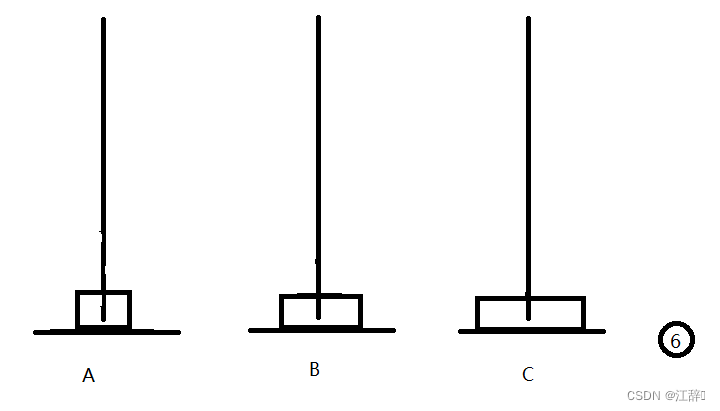
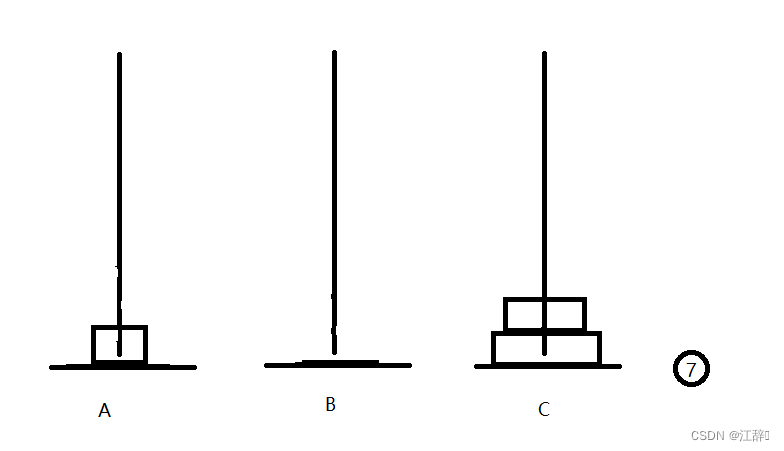
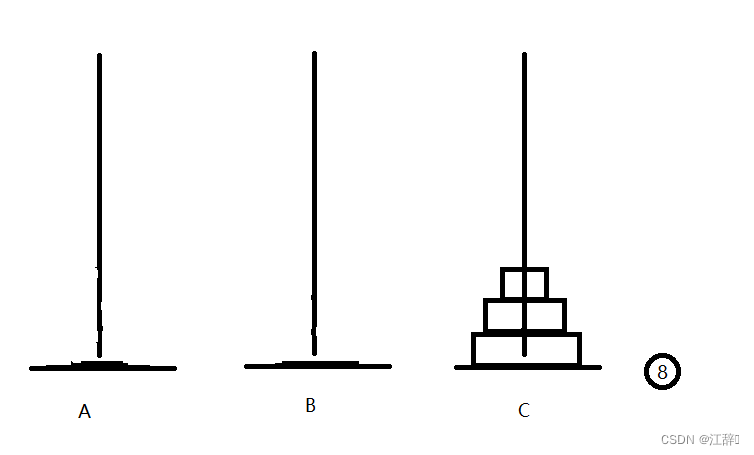
好啦,我们在汉诺塔的n等于3的时候,是这样移动盘子的,我们通过中间的中转盘b来解决我们汉诺塔问题。具体步骤如下。
我们首先以C柱为中转柱,将最上面的两个盘子移动到B柱上,之后我们将B柱作为起始柱,将一个大的汉诺塔问题化为一个小的汉诺塔问题,以A柱为中转柱重复操作。在这个过程中,n是逐渐变小的,所以我们这里可以理解为逐级的n-1。
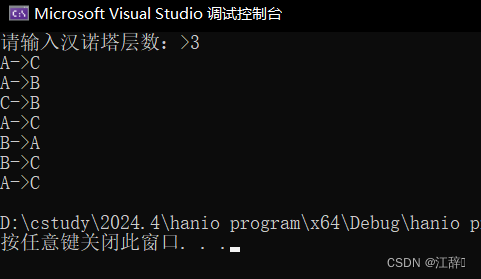
我们通过7步可以解决。
A->C
A->B
C->B
A->C
B->A
B->C
A->C
代码实现
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
//定义一个函数
void hanio(int n, char A, char B, char C)
{//设置限制条件if (n == 1){printf("%c->%c\n", A, C);}else{
//将n-1个盘子从源柱移动到辅助柱hanio(n - 1, A, C, B);printf("%c->%c\n", A, C);
//将n-1个柱子从辅助柱移动到目标柱hanio(n - 1, B, A, C);}
}
int main()
{int n;printf("请输入汉诺塔层数:>");scanf("%d", &n);hanio(n, 'A', 'B', 'C');
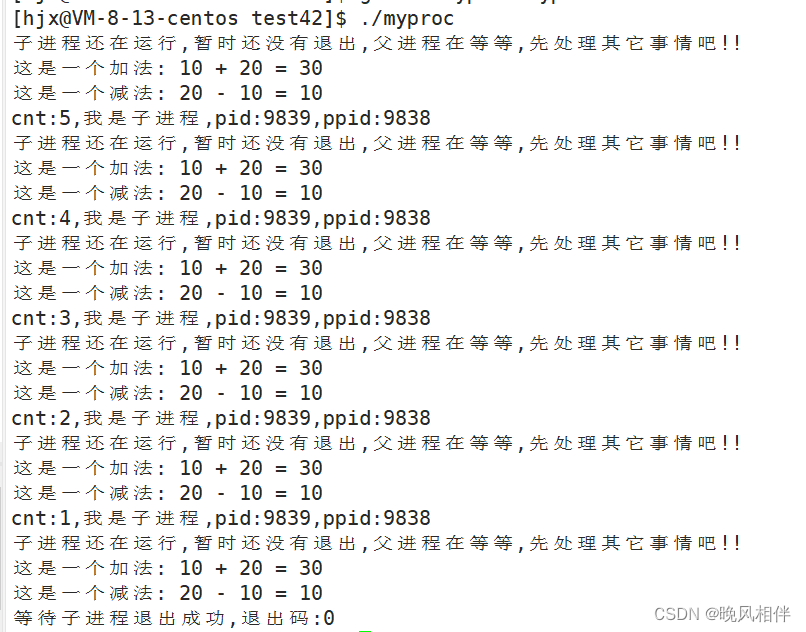
}运行结果
以3个盘子为例