机器学习(算法篇)完整教程(附代码资料)主要内容讲述:机器学习算法课程定位、目标,K-近邻算法定位,目标,学习目标,1 什么是K-近邻算法,1 Scikit-learn工具介绍,2 K-近邻算法API。K-近邻算法,1.4 k值的选择学习目标,学习目标,1 kd树简介,2 构造方法,3 案例分析,4 总结。K-近邻算法,1.6 案例:鸢尾花种类预测--数据集介绍学习目标,1 案例:鸢尾花种类预测,2 scikit-learn中数据集介绍,1 什么是特征预处理,2 归一化,3 标准化。K-近邻算法,1.8 案例:鸢尾花种类预测—流程实现学习目标,1 再识K-近邻算法API,2 案例:鸢尾花种类预测,总结,1 什么是交叉验证(cross validation),2 什么是网格搜索(Grid Search)。线性回归,2.1 线性回归简介学习目标,1 线性回归应用场景,2 什么是线性回归,1 线性回归API,2 举例,1 常见函数的导数。线性回归,2.6 梯度下降法介绍学习目标,1 全梯度下降算法(FG),2 随机梯度下降算法(SG),3 小批量梯度下降算法(mini-bantch),4 随机平均梯度下降算法(SAG),5 算法比较。线性回归,2.8 欠拟合和过拟合学习目标,1 定义,2 原因以及解决办法,3 正则化,4 维灾难【拓展知识】。线性回归,2.9 正则化线性模型学习目标,1 Ridge Regression (岭回归,又名 Tikhonov regularization),2 Lasso Regression(Lasso 回归),3 Elastic Net (弹性网络),4 Early Stopping [了解],1 API。逻辑回归,3.4 分类评估方法学习目标,1.分类评估方法,2 ROC曲线与AUC指标,3 总结,1 曲线绘制,2 意义解释。决策树算法,4.4 特征工程-特征提取学习目标,1 特征提取,2 字典特征提取,3 文本特征提取。决策树算法,4.5 决策树算法api学习目标,1 泰坦尼克号数据,2 步骤分析,3 代码过程,3 决策树可视化,学习目标。集成学习,5.3 Boosting学习目标,1.boosting集成原理,2 GBDT(了解),3.XGBoost【了解】,4 什么是泰勒展开式【拓展】,学习目标。聚类算法,6.4 模型评估学习目标,1 误差平方和(SSE \The sum of squares due to error):,2 “肘”方法 (Elbow method) — K值确定,3 轮廓系数法(Silhouette Coefficient),4 CH系数(Calinski-Harabasz Index),5 总结。聚类算法,6.6 特征降维学习目标,1 降维,2 特征选择,3 主成分分析,1 需求,2 分析。
全套笔记资料代码移步: 前往gitee仓库查看
感兴趣的小伙伴可以自取哦,欢迎大家点赞转发~
全套教程部分目录:


部分文件图片:

线性回归
学习目标
- 掌握线性回归的实现过程
- 应用LinearRegression或SGDRegressor实现回归预测
- 知道回归算法的评估标准及其公式
- 知道过拟合与欠拟合的原因以及解决方法
- 知道岭回归的原理及与线性回归的不同之处
- 应用Ridge实现回归预测
- 应用joblib实现模型的保存与加载
2.1 线性回归简介
1 线性回归应用场景
-
房价预测
-
销售额度预测
-
贷款额度预测
举例:

2 什么是线性回归
2.1 定义与公式
线性回归(Linear regression)是利用回归方程(函数)对一个或多个自变量(特征值)和因变量(目标值)之间关系进行建模的一种分析方式。
- 特点:只有一个自变量的情况称为单变量回归,多于一个自变量情况的叫做多元回归
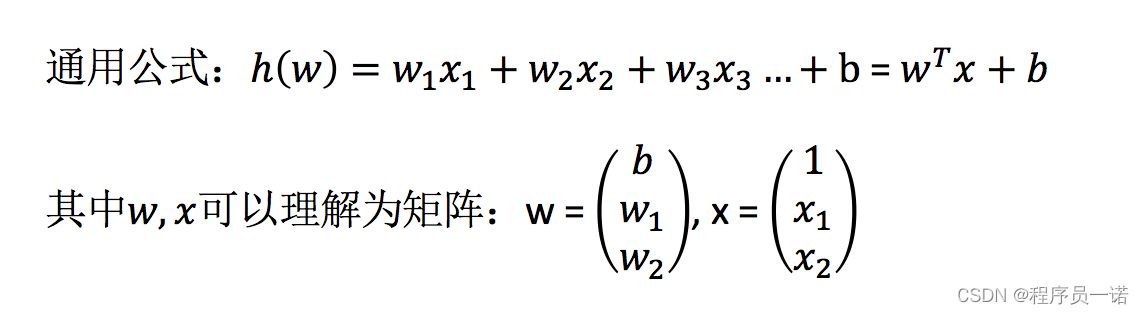
- 线性回归用矩阵表示举例

那么怎么理解呢?我们来看几个例子
- 期末成绩:0.7×考试成绩+0.3×平时成绩
- 房子价格 = 0.02×中心区域的距离 + 0.04×城市一氧化氮浓度 + (-0.12×自住房平均房价) + 0.254×城镇犯罪率
上面两个例子,我们看到特征值与目标值之间建立了一个关系,这个关系可以理解为线性模型。
2.2 线性回归的特征与目标的关系分析
线性回归当中主要有两种模型,一种是线性关系,另一种是非线性关系。在这里我们只能画一个平面更好去理解,所以都用单个特征或两个特征举例子。
-
线性关系
-
单变量线性关系:
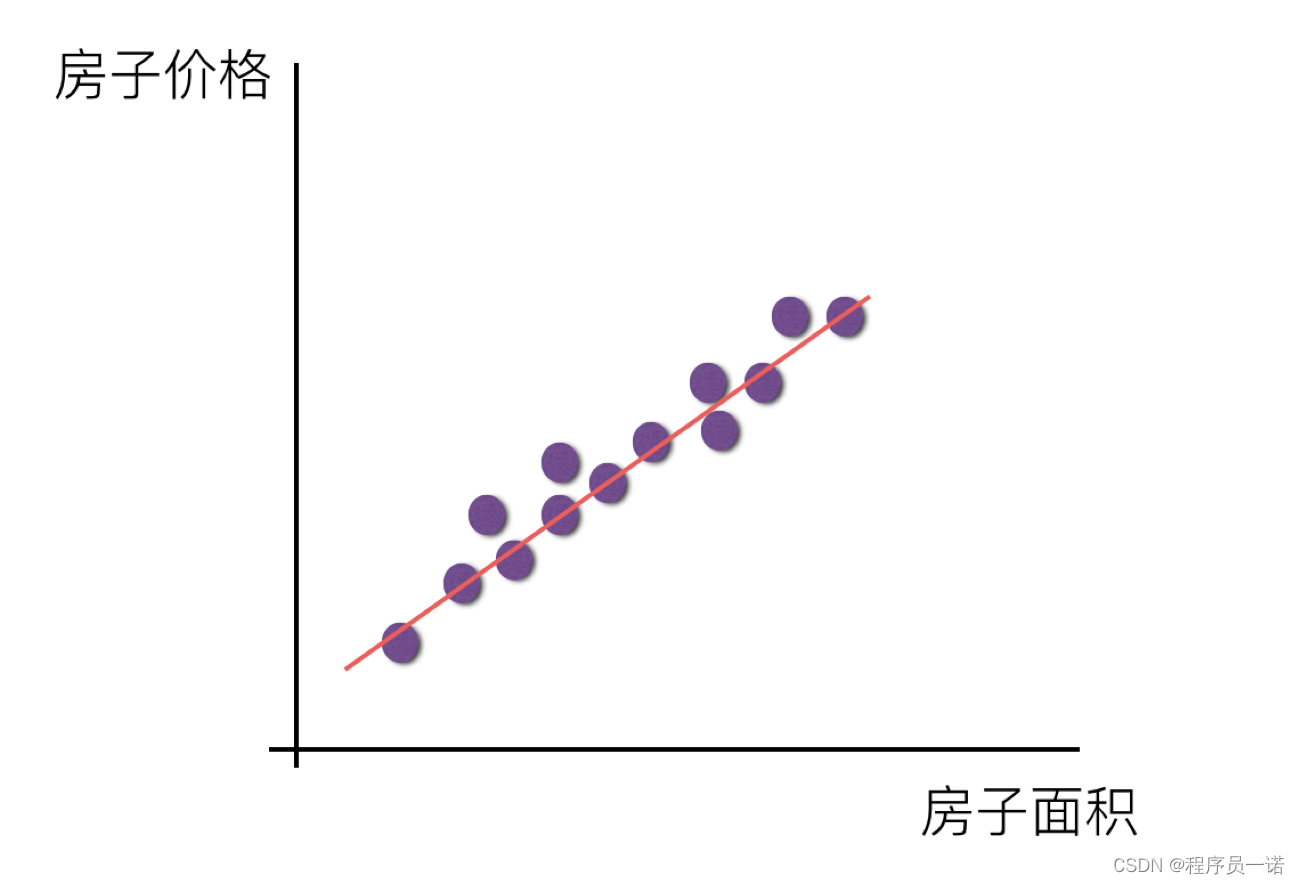
- 多变量线性关系
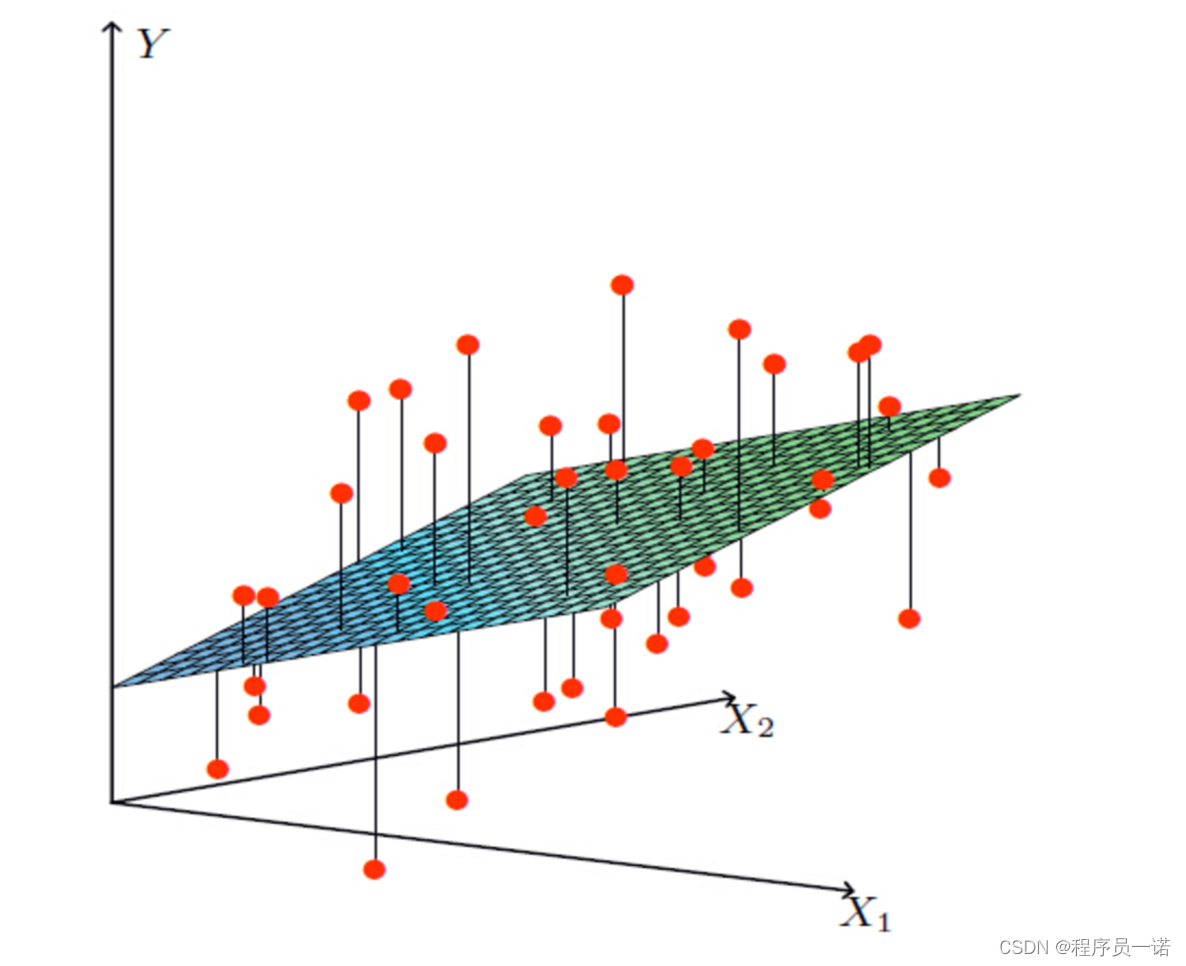
注释:单特征与目标值的关系呈直线关系,或者两个特征与目标值呈现平面的关系
更高维度的我们不用自己去想,记住这种关系即可
- 非线性关系
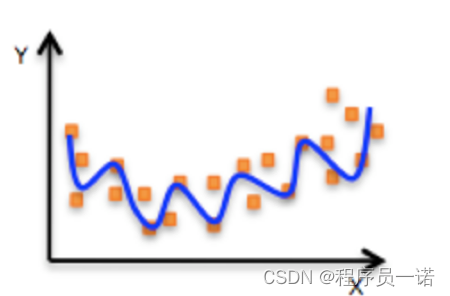
注释:为什么会这样的关系呢?原因是什么?
如果是非线性关系,那么回归方程可以理解为:w1x1+w2x2^2+w3x3^2
2.2 线性回归api初步使用
1 线性回归API
-
sklearn.linear_model.LinearRegression()
-
LinearRegression.coef_:回归系数
2 举例

2.1 步骤分析
- 1.获取数据集
- 2.数据基本处理(该案例中省略)
- 3.特征工程(该案例中省略)
- 4.机器学习
- 5.模型评估(该案例中省略)
2.2 代码过程
- 导入模块
from sklearn.linear_model import LinearRegression
- 构造数据集
x = [[80, 86],
[82, 80],
[85, 78],
[90, 90],
[86, 82],
[82, 90],
[78, 80],
[92, 94]]
y = [84.2, 80.6, 80.1, 90, 83.2, 87.6, 79.4, 93.4]
- 机器学习-- 模型训练
# 实例化APIestimator = LinearRegression()# 使用fit方法进行训练estimator.fit(x,y)estimator.coef_estimator.predict([[100, 80]])
2.3 数学:求导
1 常见函数的导数

2 导数的四则运算
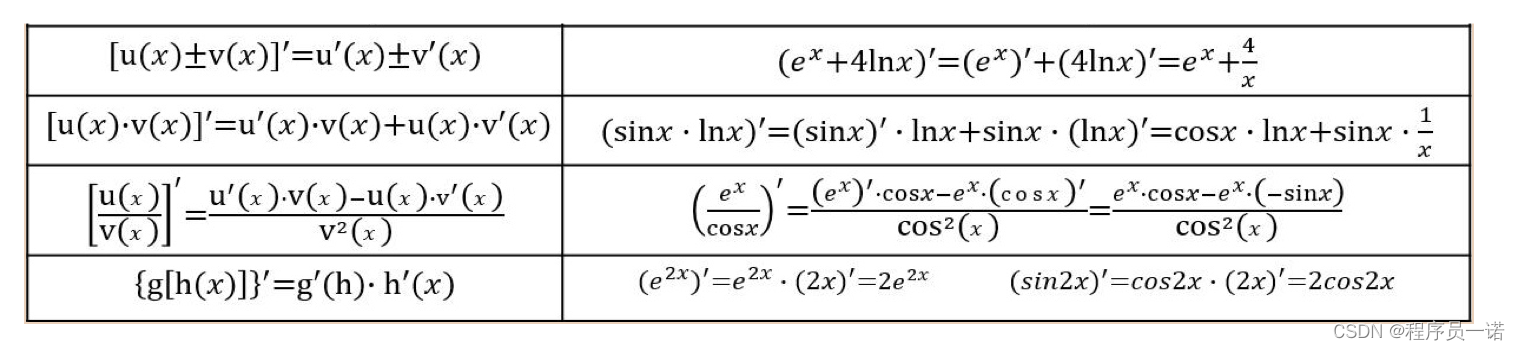
3 练习
-
3.1 y = x^3-2x^2+sinx,求f`(x)

-
3.2 y=ln(sinx), 求dy/dx
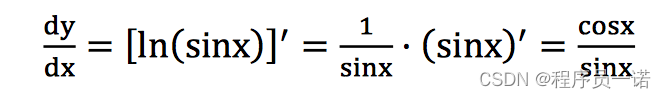
4 矩阵(向量)求导 [了解]
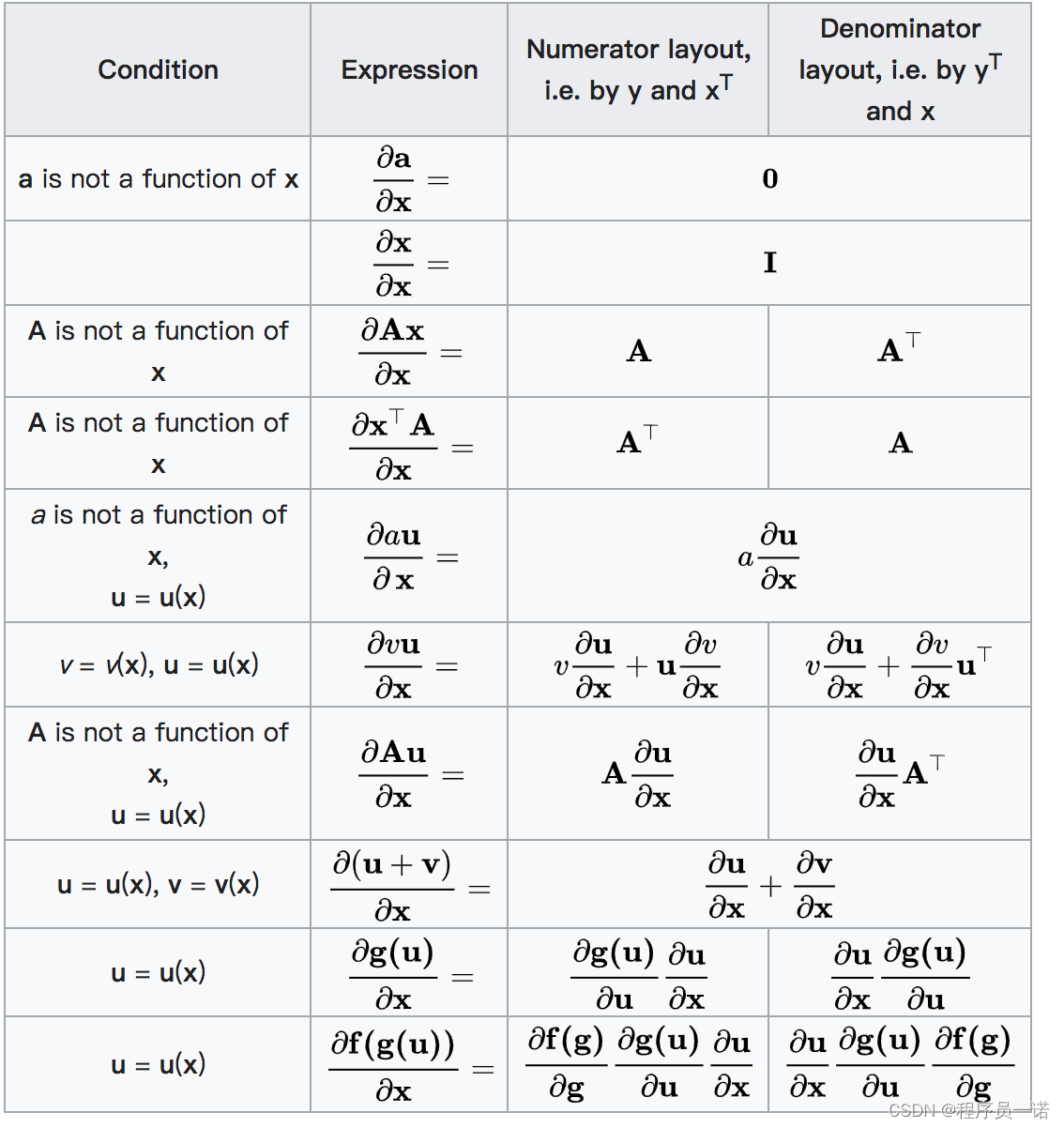
参考链接:[
线性回归
学习目标
- 掌握线性回归的实现过程
- 应用LinearRegression或SGDRegressor实现回归预测
- 知道回归算法的评估标准及其公式
- 知道过拟合与欠拟合的原因以及解决方法
- 知道岭回归的原理及与线性回归的不同之处
- 应用Ridge实现回归预测
- 应用joblib实现模型的保存与加载
2.4 线性回归的损失和优化
假设刚才的房子例子,真实的数据之间存在这样的关系
真实关系:真实房子价格 = 0.02×中心区域的距离 + 0.04×城市一氧化氮浓度 + (-0.12×自住房平均房价) + 0.254×城镇犯罪率
那么现在呢,我们随意指定一个关系(猜测)
随机指定关系:预测房子价格 = 0.25×中心区域的距离 + 0.14×城市一氧化氮浓度 + 0.42×自住房平均房价 + 0.34×城镇犯罪率
请问这样的话,会发生什么?真实结果与我们预测的结果之间是不是存在一定的误差呢?类似这样样子
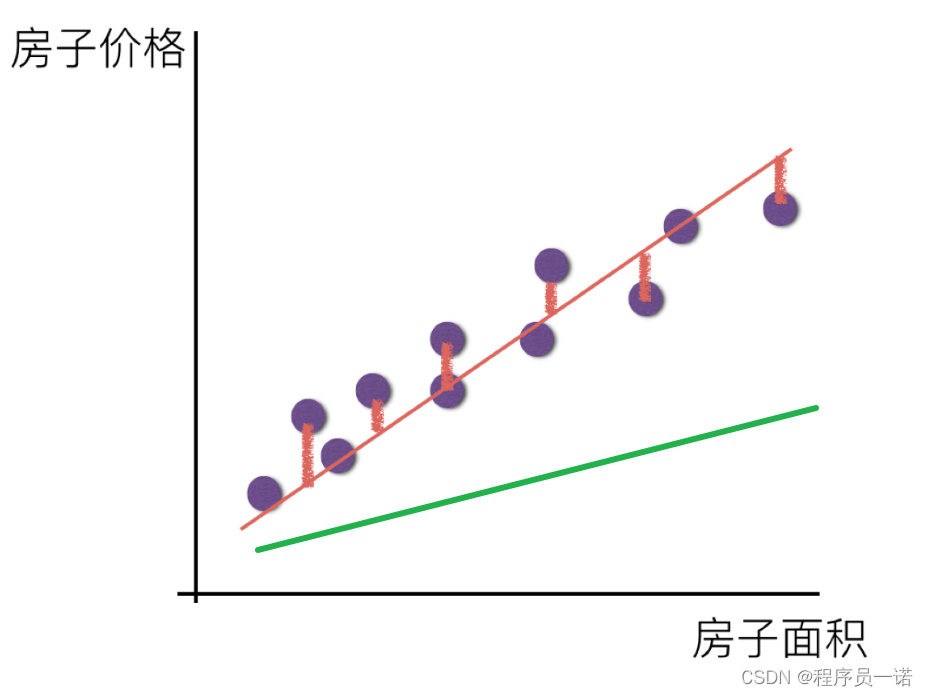
既然存在这个误差,那我们就将这个误差给衡量出来
1 损失函数
总损失定义为:
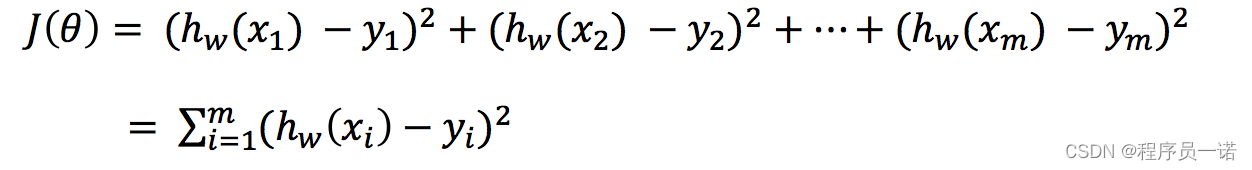
- yi为第i个训练样本的真实值
- h(xi)为第i个训练样本特征值组合预测函数
- 又称最小二乘法
如何去减少这个损失,使我们预测的更加准确些?既然存在了这个损失,我们一直说机器学习有自动学习的功能,在线性回归这里更是能够体现。这里可以通过一些优化方法去优化(其实是数学当中的求导功能)回归的总损失!!!
2 优化算法
如何去求模型当中的W,使得损失最小?(目的是找到最小损失对应的W值)
线性回归经常使用的两种优化算法
2.1 正规方程
2.1.1 什么是正规方程
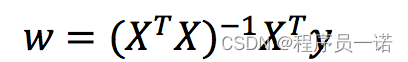
理解:X为特征值矩阵,y为目标值矩阵。直接求到最好的结果
缺点:当特征过多过复杂时,求解速度太慢并且得不到结果

2.1.2 正规方程求解举例
以下表示数据为例:

即:

运用正规方程方法求解参数:
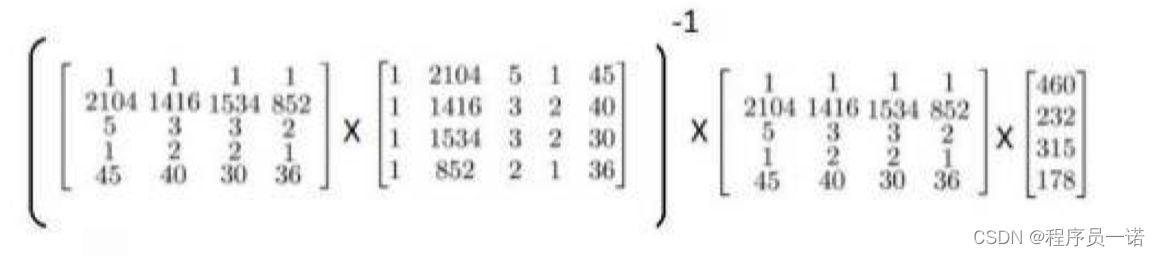
2.1.3 正规方程的推导
- 推导方式一:
把该损失函数转换成矩阵写法:

其中y是真实值矩阵,X是特征值矩阵,w是权重矩阵
对其求解关于w的最小值,起止y,X 均已知二次函数直接求导,导数为零的位置,即为最小值。
求导:

注:式(1)到式(2)推导过程中, X是一个m行n列的矩阵,并不能保证其有逆矩阵,但是右乘XT把其变成一个方阵,保证其有逆矩阵。
式(5)到式(6)推导过程中,和上类似。
- 推导方式二【拓展】:
[
2.2 梯度下降(Gradient Descent)
2.2.1 什么是梯度下降
梯度下降法的基本思想可以类比为一个下山的过程。
假设这样一个场景:一个人被困在山上,需要从山上下来(i.e. 找到山的最低点,也就是山谷)。但此时山上的浓雾很大,导致可视度很低。因此,下山的路径就无法确定,他必须利用自己周围的信息去找到下山的路径。这个时候,他就可以利用梯度下降算法来帮助自己下山。具体来说就是,以他当前的所处的位置为基准,寻找这个位置最陡峭的地方,然后朝着山的高度下降的地方走,(同理,如果我们的目标是上山,也就是爬到山顶,那么此时应该是朝着最陡峭的方向往上走)。然后每走一段距离,都反复采用同一个方法,最后就能成功的抵达山谷。
梯度下降的基本过程就和下山的场景很类似。
首先,我们有一个可微分的函数。这个函数就代表着一座山。
我们的目标就是找到这个函数的最小值,也就是山底。
根据之前的场景假设,最快的下山的方式就是找到当前位置最陡峭的方向,然后沿着此方向向下走,对应到函数中,就是找到给定点的梯度 ,然后朝着梯度相反的方向,就能让函数值下降的最快!因为梯度的方向就是函数之变化最快的方向。 所以,我们重复利用这个方法,反复求取梯度,最后就能到达局部的最小值,这就类似于我们下山的过程。而求取梯度就确定了最陡峭的方向,也就是场景中测量方向的手段。
2.2.2 梯度的概念
梯度是微积分中一个很重要的概念
在单变量的函数中,梯度其实就是函数的微分,代表着函数在某个给定点的切线的斜率
在多变量函数中,梯度是一个向量,向量有方向,梯度的方向就指出了函数在给定点的上升最快的方向
这也就说明了为什么我们需要千方百计的求取梯度!我们需要到达山底,就需要在每一步观测到此时最陡峭的地方,梯度就恰巧告诉了我们这个方向。梯度的方向是函数在给定点上升最快的方向,那么梯度的反方向就是函数在给定点下降最快的方向,这正是我们所需要的。所以我们只要沿着梯度的反方向一直走,就能走到局部的最低点!
2.2.3 梯度下降举例
- 1. 单变量函数的梯度下降**
我们假设有一个单变量的函数 :J(θ) = θ2
函数的微分:J、(θ) = 2θ
初始化,起点为: θ0= 1
学习率:α = 0.4
我们开始进行梯度下降的迭代计算过程:

如图,经过四次的运算,也就是走了四步,基本就抵达了函数的最低点,也就是山底

- 2.多变量函数的梯度下降
我们假设有一个目标函数 ::J(θ) = θ12+ θ22
现在要通过梯度下降法计算这个函数的最小值。我们通过观察就能发现最小值其实就是 (0,0)点。但是接下 来,我们会从梯度下降算法开始一步步计算到这个最小值! 我们假设初始的起点为: θ0= (1, 3)
初始的学习率为:α = 0.1
函数的梯度为:▽:J(θ) =< 2θ1,2θ2>
进行多次迭代:

我们发现,已经基本靠近函数的最小值点
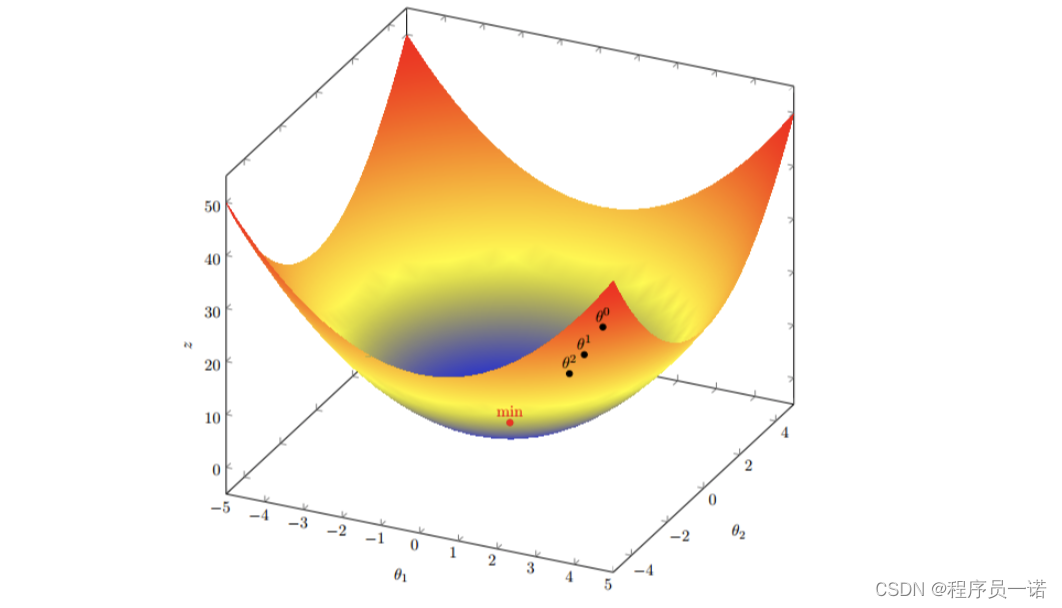
2.2.4 梯度下降(Gradient Descent)公式

- 1) α是什么含义?
α在梯度下降算法中被称作为学习率或者步长,意味着我们可以通过α来控制每一步走的距离,以保证不要步子跨的太大扯着蛋,哈哈,其实就是不要走太快,错过了最低点。同时也要保证不要走的太慢,导致太阳下山了,还没有走到山下。所以α的选择在梯度下降法中往往是很重要的!α不能太大也不能太小,太小的话,可能导致迟迟走不到最低点,太大的话,会导致错过最低点!

- 2) 为什么梯度要乘以一个负号?
梯度前加一个负号,就意味着朝着梯度相反的方向前进!我们在前文提到,梯度的方向实际就是函数在此点上升最快的方向!而我们需要朝着下降最快的方向走,自然就是负的梯度的方向,所以此处需要加上负号
我们通过两个图更好理解梯度下降的过程

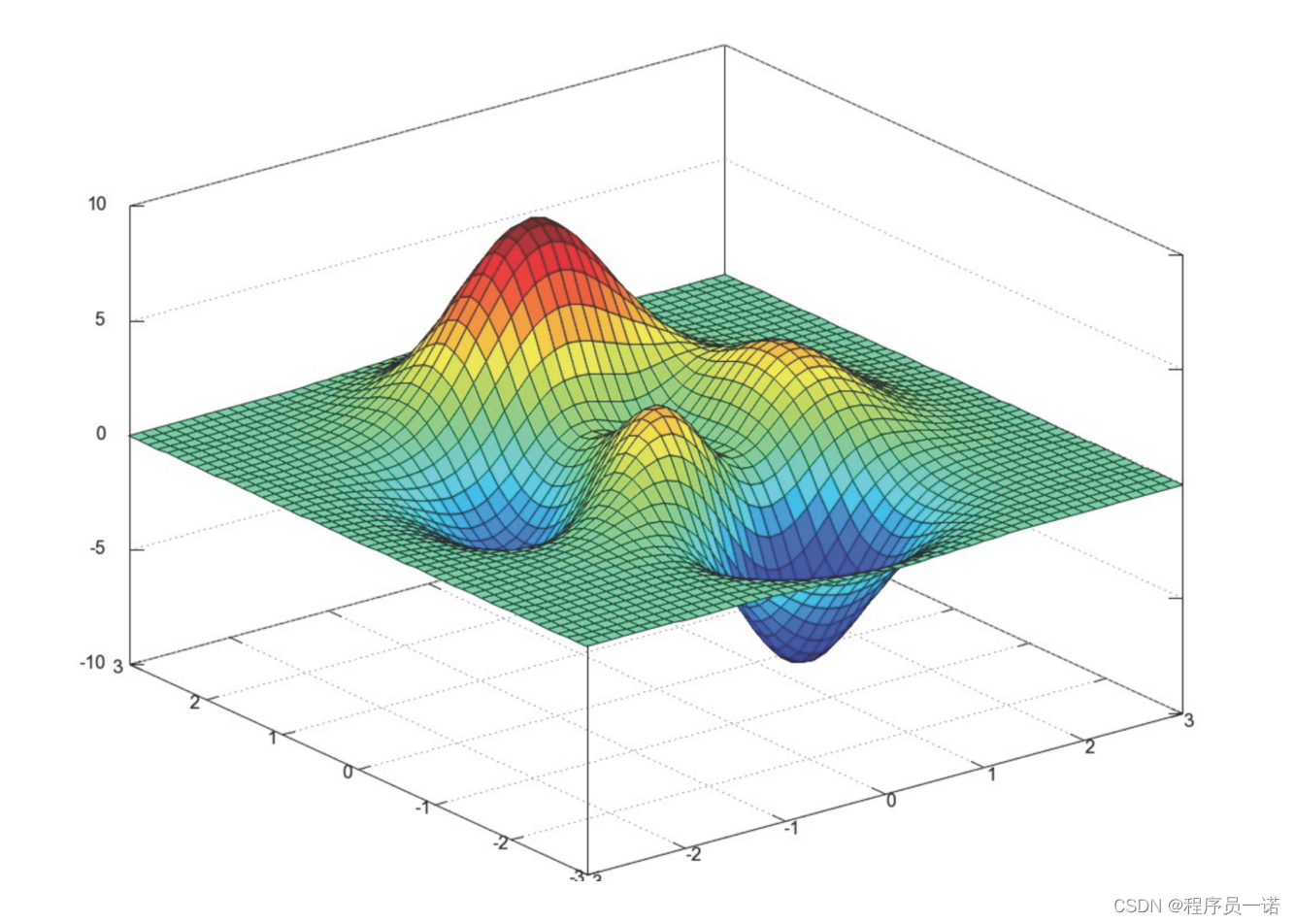
所以有了梯度下降这样一个优化算法,回归就有了"自动学习"的能力
-
优化动态图演示

- 梯度下降和正规方程的对比
| 梯度下降 | 正规方程 |
|---|---|
| 需要选择学习率 | 不需要 |
| 需要迭代求解 | 一次运算得出 |
| 特征数量较大可以使用 | 需要计算方程,时间复杂度高O(n3) |
-
选择:
-
小规模数据:
- LinearRegression(不能解决拟合问题)
- 岭回归
-
大规模数据:SGDRegressor