给定一个链表的头节点  head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改 链表。

示例 1：

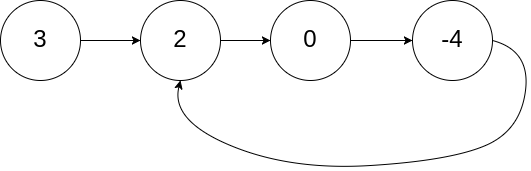
输入：head = [3,2,0,-4], pos = 1
输出：返回索引为 1 的链表节点
解释：链表中有一个环，其尾部连接到第二个节点。

示例 2：

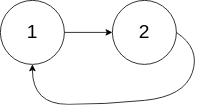
输入：head = [1,2], pos = 0
输出：返回索引为 0 的链表节点
解释：链表中有一个环，其尾部连接到第一个节点。

示例 3：

输入：head = [1], pos = -1
输出：返回 null
解释：链表中没有环。

提示：

• 链表中节点的数目范围在范围 [0, 104] 内
• -105 <= Node.val <= 105
• pos 的值为 -1 或者链表中的一个有效索引

进阶：你是否可以使用 O(1) 空间解决此题？

解题思路：

主要得出结论：

1.slow指针和fast指针都向后移动，当slow指针和fast指针相遇时，表示链表中有环。

2.当相遇时，定义index1指针指向头结点，index2结点指向相遇时的结点，index1和index2同时向后移动，当index1和index2指针相遇时，表示找了环形入口的起点。

动画如下：

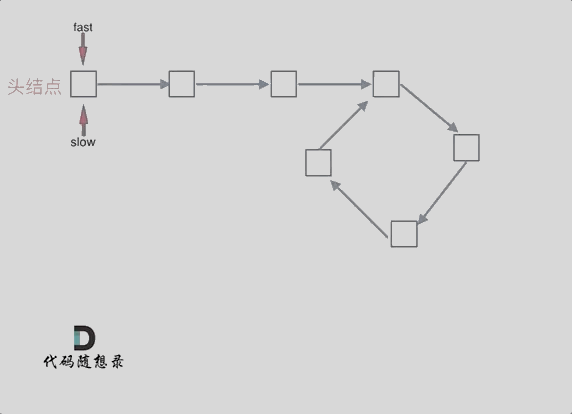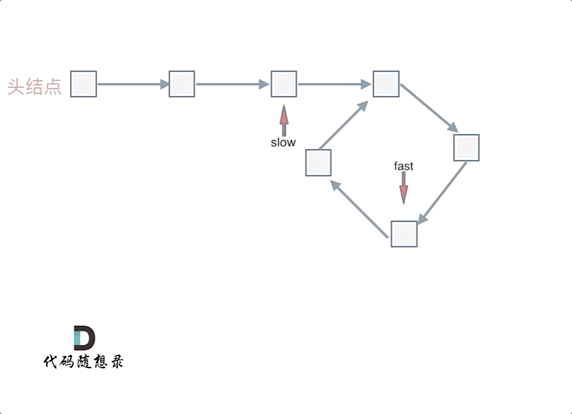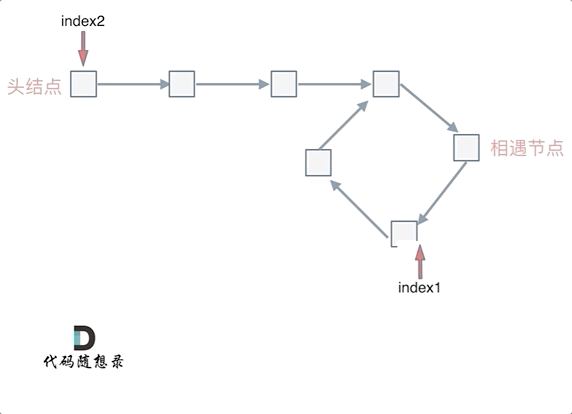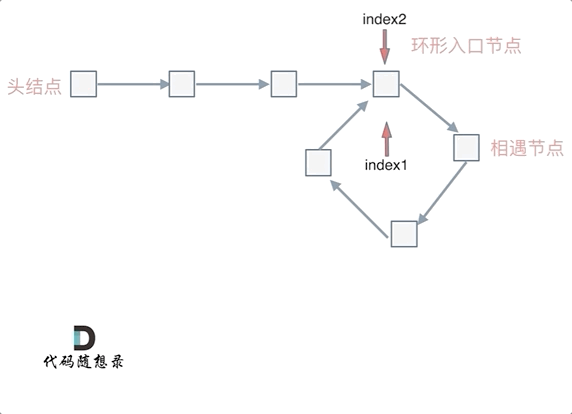
推导过程如下：

（From：代码随想录）

这道题目，不仅考察对链表的操作，而且还需要一些数学运算。

主要考察两知识点：

• 判断链表是否环
• 如果有环，如何找到这个环的入口

#判断链表是否有环

可以使用快慢指针法，分别定义 fast 和 slow 指针，从头结点出发，fast指针每次移动两个节点，slow指针每次移动一个节点，如果 fast 和 slow指针在途中相遇 ，说明这个链表有环。

为什么fast 走两个节点，slow走一个节点，有环的话，一定会在环内相遇呢，而不是永远的错开呢

首先第一点：fast指针一定先进入环中，如果fast指针和slow指针相遇的话，一定是在环中相遇，这是毋庸置疑的。

那么来看一下，为什么fast指针和slow指针一定会相遇呢？

可以画一个环，然后让 fast指针在任意一个节点开始追赶slow指针。

会发现最终都是这种情况， 如下图：

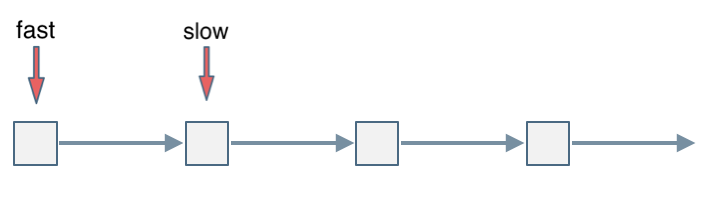
fast和slow各自再走一步， fast和slow就相遇了

这是因为fast是走两步，slow是走一步，其实相对于slow来说，fast是一个节点一个节点的靠近slow的，所以fast一定可以和slow重合。

动画如下：

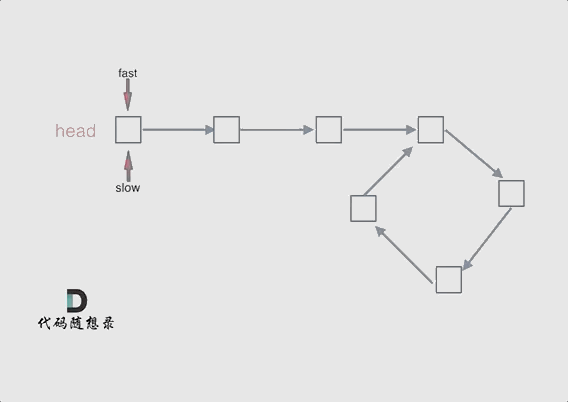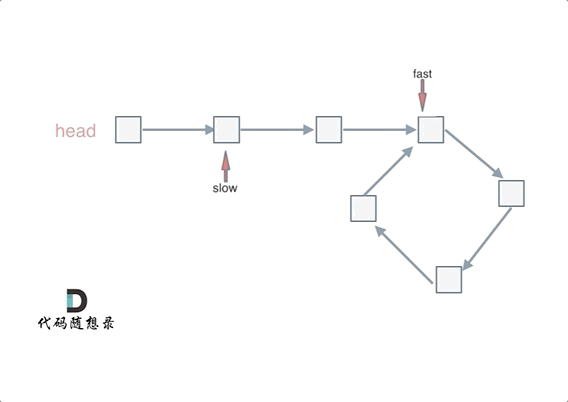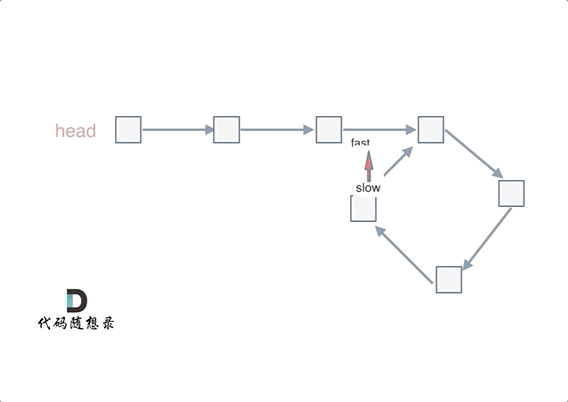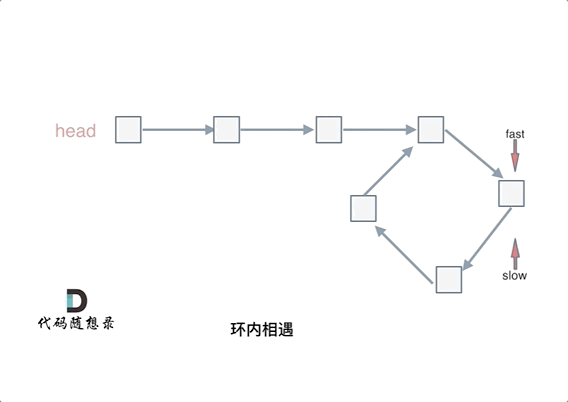
#如果有环，如何找到这个环的入口

此时已经可以判断链表是否有环了，那么接下来要找这个环的入口了。

假设从头结点到环形入口节点 的节点数为x。 环形入口节点到 fast指针与slow指针相遇节点 节点数为y。 从相遇节点 再到环形入口节点节点数为 z。 如图所示：

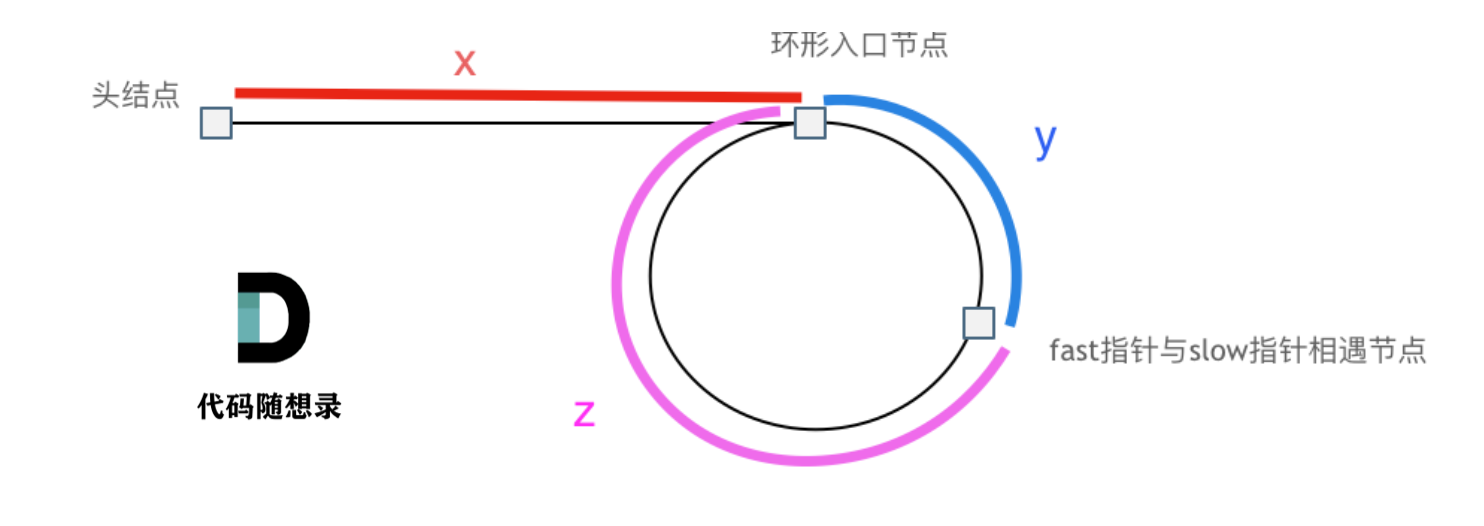
那么相遇时： slow指针走过的节点数为: x + y， fast指针走过的节点数：x + y + n (y + z)，n为fast指针在环内走了n圈才遇到slow指针， （y+z）为 一圈内节点的个数A。

因为fast指针是一步走两个节点，slow指针一步走一个节点， 所以 fast指针走过的节点数 = slow指针走过的节点数 * 2：

(x + y) * 2 = x + y + n (y + z)

两边消掉一个（x+y）: x + y = n (y + z)

因为要找环形的入口，那么要求的是x，因为x表示 头结点到 环形入口节点的的距离。

所以要求x ，将x单独放在左面：x = n (y + z) - y ,

再从n(y+z)中提出一个 （y+z）来，整理公式之后为如下公式：x = (n - 1) (y + z) + z 注意这里n一定是大于等于1的，因为 fast指针至少要多走一圈才能相遇slow指针。

这个公式说明什么呢？

先拿n为1的情况来举例，意味着fast指针在环形里转了一圈之后，就遇到了 slow指针了。

当 n为1的时候，公式就化解为 x = z，

这就意味着，从头结点出发一个指针，从相遇节点 也出发一个指针，这两个指针每次只走一个节点， 那么当这两个指针相遇的时候就是 环形入口的节点。

也就是在相遇节点处，定义一个指针index1，在头结点处定一个指针index2。

让index1和index2同时移动，每次移动一个节点， 那么他们相遇的地方就是 环形入口的节点。

动画如下：

那么 n如果大于1是什么情况呢，就是fast指针在环形转n圈之后才遇到 slow指针。

其实这种情况和n为1的时候 效果是一样的，一样可以通过这个方法找到 环形的入口节点，只不过，index1 指针在环里 多转了(n-1)圈，然后再遇到index2，相遇点依然是环形的入口节点。

代码如下：

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     ListNode *next;*     ListNode(int x) : val(x), next(NULL) {}* };*/
class Solution {
public:ListNode *detectCycle(ListNode *head) {ListNode* fast = head;ListNode* slow = head;while(fast != NULL && fast->next != NULL) {slow = slow->next;fast = fast->next->next;// 快慢指针相遇，此时从head 和 相遇点，同时查找直至相遇if (slow == fast) {ListNode* index1 = fast;ListNode* index2 = head;while (index1 != index2) {index1 = index1->next;index2 = index2->next;}return index2; // 返回环的入口}}return NULL;}
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

• 时间复杂度: O(n)，快慢指针相遇前，指针走的次数小于链表长度，快慢指针相遇后，两个index指针走的次数也小于链表长度，总体为走的次数小于 2n
• 空间复杂度: O(1)

#补充

在推理过程中，大家可能有一个疑问就是：为什么第一次在环中相遇，slow的 步数 是 x+y 而不是 x + 若干环的长度 + y 呢？

即文章链表：环找到了，那入口呢？ (opens new window)中如下的地方：

首先slow进环的时候，fast一定是先进环来了。

如果slow进环入口，fast也在环入口，那么把这个环展开成直线，就是如下图的样子：

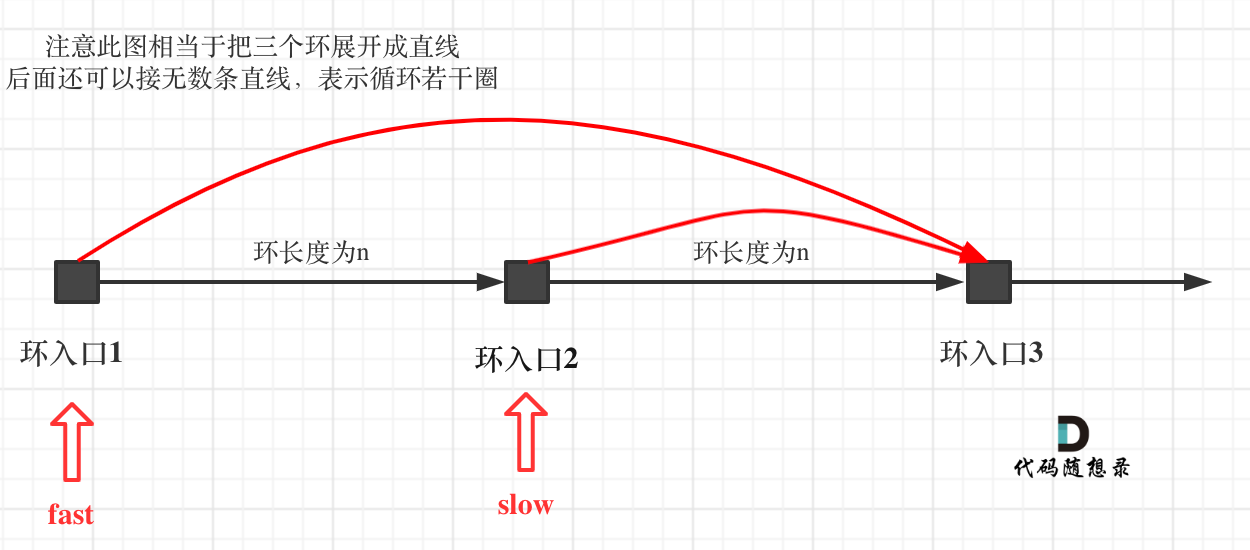
可以看出如果slow 和 fast同时在环入口开始走，一定会在环入口3相遇，slow走了一圈，fast走了两圈。

重点来了，slow进环的时候，fast一定是在环的任意一个位置，如图：

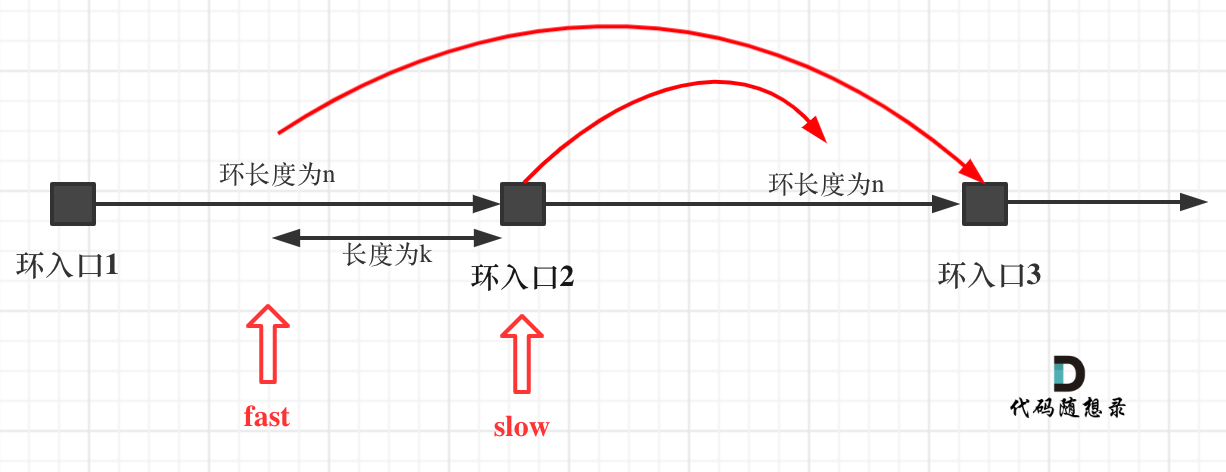
那么fast指针走到环入口3的时候，已经走了k + n 个节点，slow相应的应该走了(k + n) / 2 个节点。

因为k是小于n的（图中可以看出），所以(k + n) / 2 一定小于n。

也就是说slow一定没有走到环入口3，而fast已经到环入口3了。

这说明什么呢？

在slow开始走的那一环已经和fast相遇了。

那有同学又说了，为什么fast不能跳过去呢？ 在刚刚已经说过一次了，fast相对于slow是一次移动一个节点，所以不可能跳过去。

好了，这次把为什么第一次在环中相遇，slow的 步数 是 x+y 而不是 x + 若干环的长度 + y ，用数学推理了一下，算是对链表：环找到了，那入口呢？ (opens new window)的补充。

代码如下：

/*** Definition for singly-linked list.* class ListNode {*     int val;*     ListNode next;*     ListNode(int x) {*         val = x;*         next = null;*     }* }*/
public class Solution {public ListNode detectCycle(ListNode head) {ListNode slow = head;ListNode fast = head;while(fast != null && fast.next != null) {slow = slow.next;fast = fast.next.next;if(slow == fast) {ListNode index1 = fast;ListNode index2 = head;while(index1 != index2) {index1 = index1.next;index2 = index2.next;}return index1;}}return null;}
}