[python] Numpy库用法（持续更新）

先导入一下

import numpy as np

一、np.random用法

生成随机整数：np.random.randint(low, high, size)
- low: 最小值
- high: 最大值
- size: 生成的数组大小（可以是多维，下面同理）
生成随机浮点数：np.random.uniform(low, high, size)
- low: 最小值
- high: 最大值
- size: 生成的数组大小

在NumPy中，np.random.uniform这个函数的名称中的"uniform"指的是均匀分布（Uniform Distribution）。这种分布中，所有数值在一定范围内出现的概率是均等的，也就是说，这个范围内的任何一个数被选中的机会都是一样的。这和其他一些分布不同，比如正态分布，其中某些数值出现的机率比其他数值高。

具体来说，当你使用np.random.uniform(low, high, size)时：

low和high参数定义了数值的范围，其中low是下限（包含），high是上限（不包含）。
size参数决定了生成多少个这样的随机数。

举个例子，如果你调用np.random.uniform(1, 5, 3)，NumPy将会生成一个数组，包含3个在1（包含）到5（不包含）之间均匀分布的随机浮点数。

因此，这个函数被命名为"uniform"，正是因为它生成的是遵循均匀分布规律的随机数。

生成服从正态分布的随机数：np.random.normal(loc, scale, size)
- loc: 均值
- scale: 标准差
- size: 生成的数组大小
生成一个随机排列：np.random.permutation(x)
- x: 输入的数组或整数
生成一个随机样本：np.random.sample(size)
- size: 生成的数组大小
生成一个随机种子：np.random.seed(seed)
- seed: 种子值
生成一个符合指定概率分布的随机数：np.random.choice(a, size, replace, p)
- a: 输入的数组
- size: 生成的数组大小
- replace: 是否可以重复抽样
- p: 每个元素被抽样的概率
生成一个随机数组成的矩阵：np.random.rand(d0, d1, ..., dn)
- d0, d1, ..., dn: 矩阵的维度
生成一个随机整数矩阵：np.random.randint(low, high, size)
- low: 最小值
- high: 最大值
- size: 生成的矩阵大小

import numpy as np# 生成一个随机整数
random_int = np.random.randint(1, 10, 5)
print(random_int)# 生成一个随机浮点数
random_float = np.random.uniform(1.0, 5.0, 5)
print(random_float)# 生成一个服从正态分布的随机数
random_normal = np.random.normal(0, 1, 5)
print(random_normal)# 生成一个随机排列
random_permutation = np.random.permutation([1, 2, 3, 4, 5])
print(random_permutation)# 生成一个随机样本
random_sample = np.random.sample(5)
print(random_sample)# 生成一个随机种子
np.random.seed(0)
random_seed = np.random.rand(3)
print(random_seed)# 生成一个符合指定概率分布的随机数
random_choice = np.random.choice([1, 2, 3, 4, 5], 3, replace=False, p=[0.1, 0.2, 0.3, 0.2, 0.2])
print(random_choice)# 生成一个随机矩阵
random_matrix = np.random.rand(2, 3)
print(random_matrix)# 生成一个随机整数矩阵
random_int_matrix = np.random.randint(1, 10, (2, 3))
print(random_int_matrix)# 生成一个服从均匀分布的随机数
random_uniform = np.random.rand(2, 3)
print(random_uniform)

输出结果

[9 6 4 8 5]
[1.87678294 4.17125097 4.34816045 4.56395443 1.99147984]
[-0.27015379 -1.82642694  0.96417976  1.38643896  0.23534789]
[5 1 3 2 4]
[0.73823778 0.70459439 0.67601929 0.45422436 0.67000757]
[0.5488135  0.71518937 0.60276338]
[3 4 2]
[[0.891773   0.96366276 0.38344152][0.79172504 0.52889492 0.56804456]]
[[6 9 5][4 1 4]]
[[0.95715516 0.14035078 0.87008726][0.47360805 0.80091075 0.52047748]]

二.一些数据处理函数

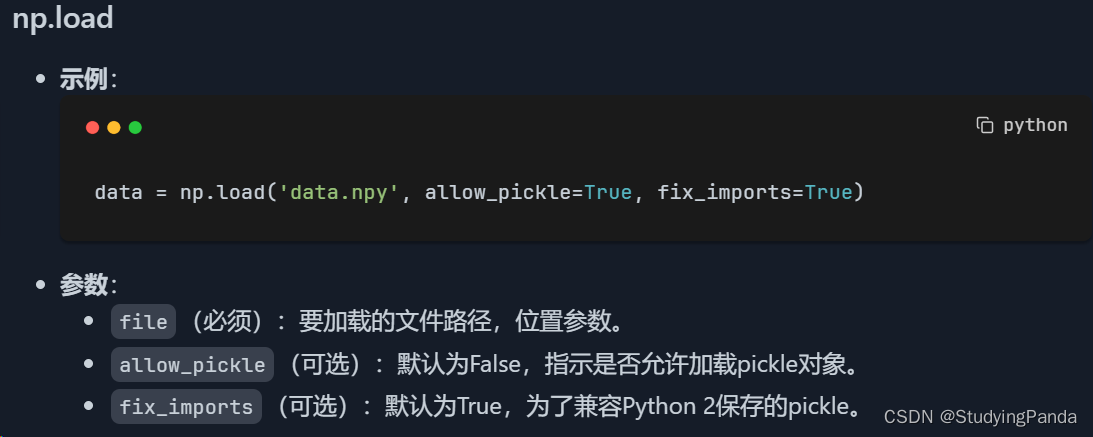
np.load

用途：这个函数用于加载存储在.npy文件中的NumPy数组。这是一种高效存储和读取NumPy数组数据的方式，特别适用于持久化大型数组。

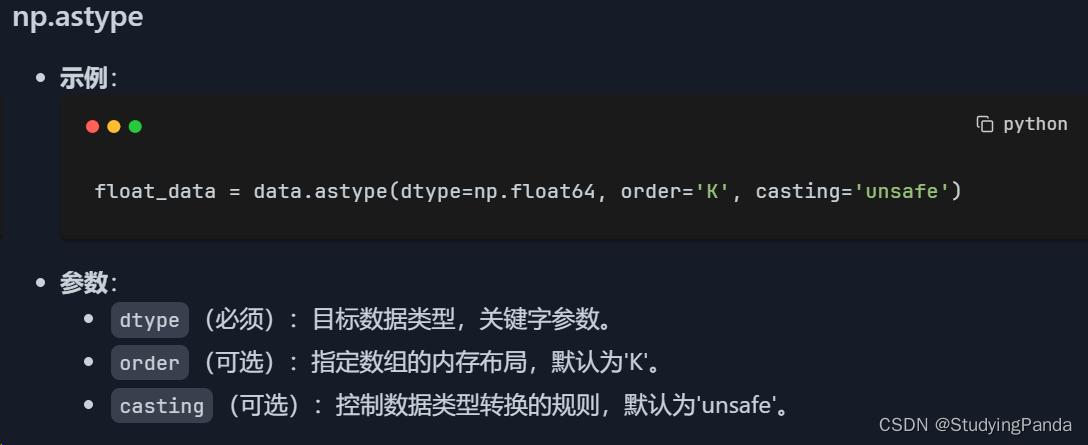
np.astype

用途：astype方法允许你复制数组并将其元素转换为一个指定的类型。这在数据处理中非常常见，比如将整数数组转换为浮点数数组，或者将浮点数数组转换为整数数组。类型转换是数据预处理的一个重要步骤。

np.shape 和 .shape

用途：这些用法提供了一种获取NumPy数组维度的方法。np.shape是一个函数，而.shape是数组对象的一个属性。了解数组的形状对于进行数组操作（如重塑或切片）是非常重要的。

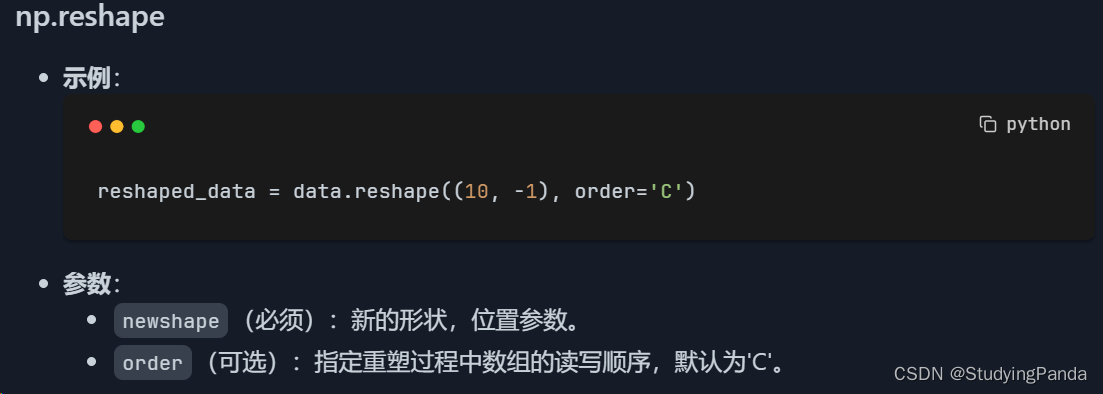
np.reshape

用途：reshape方法允许在不更改数组数据的前提下，给数组一个新的形状。这在将数据准备为特定格式进行机器学习模型训练时尤其有用。

np.std

用途：这个函数计算沿指定轴的标准差，是度量数据分散程度的一个重要统计量。在数据分析和科学研究中，标准差用于衡量数值的波动程度。

np.mean

用途：mean函数计算沿指定轴的平均值。平均值是最常用的统计量之一，用于描述数据集中趋势的中心位置。

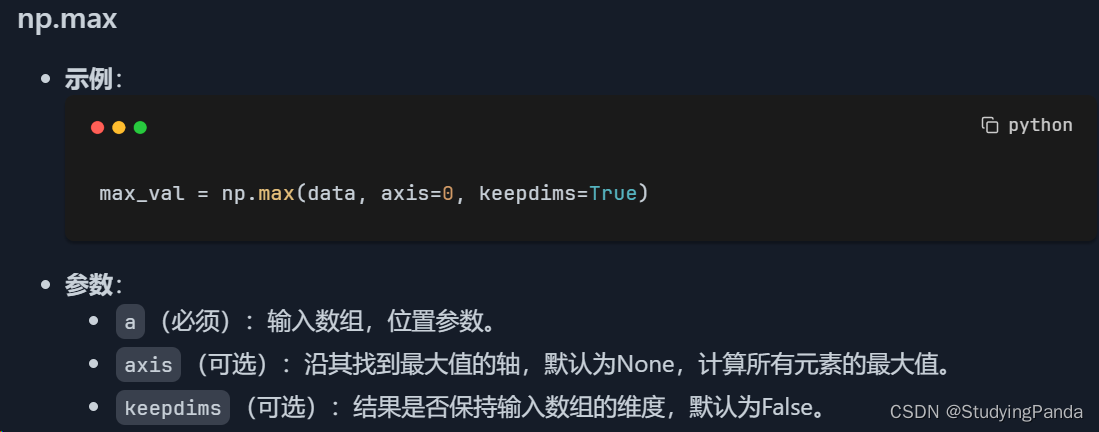
np.max

用途：这个函数计算沿指定轴的最大值。在数据分析中，了解数据的范围（最大值和最小值）对于评估数据的分布和极值非常重要。

np.arange

用途：arange函数返回一个有等差数列构成的数组。这个函数非常适用于生成序列数据，例如生成连续的时间点序列。它是Python内置range函数的NumPy版本，但可以生成浮点序列并具有更多的灵活性。

val_X.reshape(val_X.shape[0], -1)的操作并不是将数组重塑为一维数组，而是重塑为二维数组，其中第一维度保持不变，第二维度自动计算以包含剩余的所有元素。

具体来说：

val_X.shape[0]：这是val_X数组的第一个维度的大小，即行数。
-1：这个参数告诉NumPy自动计算第二个维度的大小，以便保持所有数据元素的总数不变。

例如，如果val_X原来的形状是(100, 2, 3)，这表示有100个2x3的矩阵。执行val_X.reshape(val_X.shape[0], -1)后，形状将变为(100, 6)，这意味着每个原始的2x3矩阵现在被展平成一个包含6个元素的一维数组，但在更大框架下，它们作为100行的二维数组存在。

因此，reshape操作并没有创建一个真正的一维数组，而是创建了一个二维数组，其第一维保持为原数组的行数，第二维展平了原有的每个子矩阵。

假设我们有一个数组test_Y，它表示某种测试数据的标签，如下所示：

test_Y = np.array([1, 2, 1, 3, 2, 1, 3])

我们想要找出所有标签等于1的数据的索引。在这个例子中，y的值设为1。

首先，np.arange(num_data)生成一个从0开始的等差数列。假设num_data等于test_Y的长度，即7，那么生成的数组就是[0, 1, 2, 3, 4, 5, 6]。
接下来，test_Y == 1生成一个布尔数组，表示test_Y中每个位置的值是否等于1。对于我们的test_Y，结果是：

[True, False, True, False, False, True, False]

这意味着在位置0、2和5的值等于1。
最后，通过使用上一步生成的布尔数组作为索引，我们从步骤1生成的等差数列中选择索引。因此，np.arange(num_data)[test_Y == 1]的结果将是：

[0, 2, 5]

这个结果告诉我们，在test_Y数组中，值等于1的元素位于原数组的第0、第2和第5个位置。