文章目录
- 1 转动坐标系
- 2 运动坐标系
- 3 刚体运动参数
• 拉格朗日建立机器人动力学方程需用齐次变换矩阵,计算效率低。优点是可以写成状态方程的形式,便于运用控制方法。
• 牛顿—欧拉动力学方程可得到一组正向和反向递推方程,显著优点是可把驱动力矩的计算时间缩短到可实时控制的程度。
1 转动坐标系
设有两个坐标系, O X Y Z OXYZ OXYZ—惯性系, O X ∗ Y ∗ Z ∗ OX^{*}Y^{*}Z^{*} OX∗Y∗Z∗—转动系,O点重合,OX*、OY*、OZ* 相对于OX、OY、OZ旋转( O X ∗ Y ∗ Z ∗ OX^{*}Y^{*}Z^{*} OX∗Y∗Z∗相对于OXYZ 旋转)。
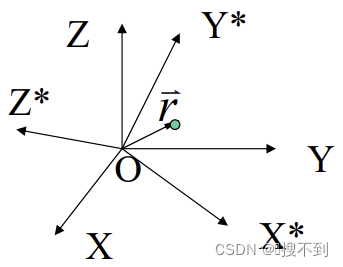
矢量 r ⃗ \vec{r} r,在 O X Y Z OXYZ OXYZ中有:
r ⃗ = x i ⃗ + y j ⃗ + z k ⃗ ( 1 ) \vec{r}=x\vec{i}+y\vec{j}+z\vec{k} \qquad(1) r=xi+yj+zk(1)
在 O X ∗ Y ∗ Z ∗ OX^{*}Y^{*}Z^{*} OX∗Y∗Z∗中有:
r ⃗ = x ∗ i ⃗ ∗ + y ∗ j ⃗ ∗ + z ∗ k ⃗ ∗ ( 2 ) \vec{r}=x^*\vec{i}^*+y^*\vec{j}^*+z^*\vec{k}^* \qquad(2) r=x∗i∗+y∗j∗+z∗k∗(2)
式(1)对时间t求导数:
d r ⃗ d t = x ˙ i ⃗ + y ˙ j ⃗ + z ˙ k ⃗ + x d i ⃗ d t + y d j ⃗ d t + z d k ⃗ d t ( 3 ) \frac{d\vec{r}}{dt}=\dot{x}\vec{i}+\dot{y}\vec{j}+\dot{z}\vec{k}+x\frac{d\vec{i}}{dt}+y\frac{d\vec{j}}{dt}+z\frac{d\vec{k}}{dt} \qquad(3) dtdr=x˙i+y˙j+z˙k+xdtdi+ydtdj+zdtdk(3)
式(2)在 O X ∗ Y ∗ Z ∗ OX^{*}Y^{*}Z^{*} OX∗Y∗Z∗中对时间t求导数:
d ∗ r ˉ d t = x ˙ ∗ i ⃗ ∗ + y ˙ ∗ j ⃗ ∗ + z ˙ ∗ k ⃗ ∗ + x ∗ d ∗ i ⃗ ∗ d t + y ∗ d ∗ j ⃗ ∗ d t + z ∗ d ∗ k ⃗ ∗ d t = x ˙ ∗ i ˉ ∗ + y ˙ ∗ j ˉ ∗ + z ˙ ∗ k ˉ ∗ ( 4 ) \begin{aligned}\frac{d^*\bar{r}}{dt}&=\dot{x}^*\vec{i}^*+\dot{y}^*\vec{j}^*+\dot{z}^*\vec{k}^*+x^*\frac{d^*\vec{i}^*}{dt}+y^*\frac{d^*\vec{j}^*}{dt}+z^*\frac{d^*\vec{k}^*}{dt}\\&=\dot{x}^*\bar{i}^*+\dot{y}^*\bar{j}^*+\dot{z}^*\bar{k}^*\end{aligned} \qquad(4) dtd∗rˉ=x˙∗i∗+y˙∗j∗+z˙∗k∗+x∗dtd∗i∗+y∗dtd∗j∗+z∗dtd∗k∗=x˙∗iˉ∗+y˙∗jˉ∗+z˙∗kˉ∗(4)
式(2)在 O X Y Z OXYZ OXYZ中对时间t求导数,并将式(4)代入:
d r ⃗ d t = x ˙ ∗ i ⃗ ∗ + y ˙ ∗ j ⃗ ∗ + z ˙ ∗ k ⃗ ∗ + x ∗ d i ⃗ ∗ d t + y ∗ d j ⃗ ∗ d t + z ∗ d k ⃗ ∗ d t = d ∗ r ⃗ d t + x ∗ d i ⃗ ∗ d t + y ∗ d j ⃗ ∗ d t + z ∗ d k ⃗ ∗ d t ( 5 ) \begin{aligned}\frac{d\vec{r}}{dt}&=\dot{x}^*\vec{i}^*+\dot{y}^*\vec{j}^*+\dot{z}^*\vec{k}^*+x^*\frac{d\vec{i}^*}{dt}+y^*\frac{d\vec{j}^*}{dt}+z^*\frac{d\vec{k}^*}{dt}\\&=\frac{d^*\vec{r}}{dt}+x^*\frac{d\vec{i}^*}{dt}+y^*\frac{d\vec{j}^*}{dt}+z^*\frac{d\vec{k}^*}{dt}\end{aligned} \qquad(5) dtdr=x˙∗i∗+y˙∗j∗+z˙∗k∗+x∗dtdi∗+y∗dtdj∗+z∗dtdk∗=dtd∗r+x∗dtdi∗+y∗dtdj∗+z∗dtdk∗(5)
设在 O X ∗ Y ∗ Z ∗ OX^{*}Y^{*}Z^{*} OX