216. 组合总和 III
思路:
本题就是在[1,2,3,4,5,6,7,8,9]这个集合中找到和为n的k个数的组合。
相对于 77. 组合,无非就是多了一个限制,本题是要找到和为n的k个数的组合,而整个集合已经是固定的了[1,...,9]。
本题k相当于树的深度,9(因为整个集合就是9个数)就是树的宽度。
例如 k = 2,n = 4的话,就是在集合[1,2,3,4,5,6,7,8,9]中求 k(个数) = 2, n(和) = 4的组合。
选取过程如图:

图中,可以看出,只有最后取到集合(1,3)和为4 符合条件。
剪枝优化:
这道题目,剪枝操作其实是很容易想到了,想必大家看上面的树形图的时候已经想到了。
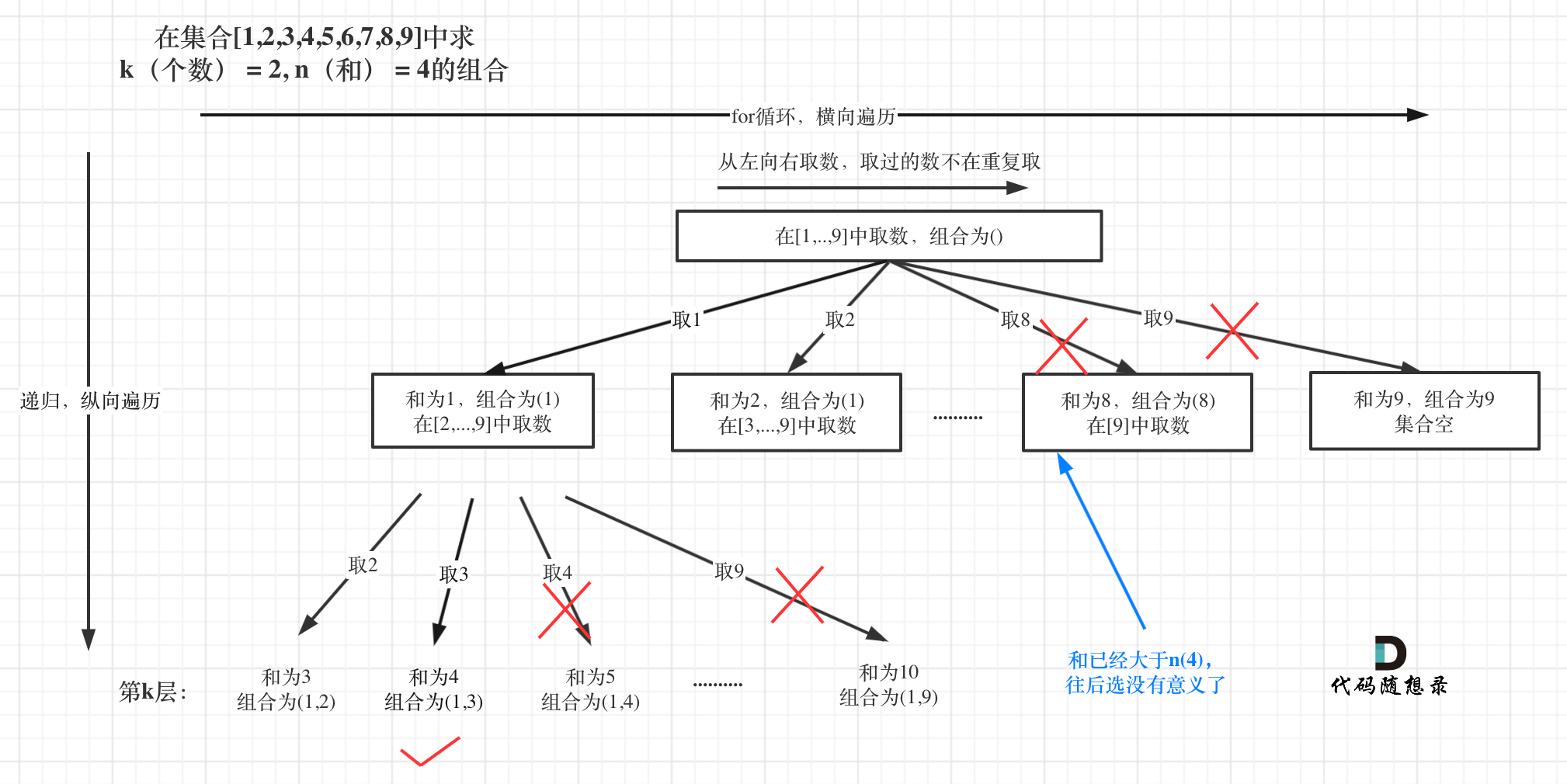
已选元素总和如果已经大于n(图中数值为4)了,那么往后遍历就没有意义了,直接剪掉。
和回溯算法:组合问题再剪剪枝 (opens new window)一样,for循环的范围也可以剪枝,i <= 9 - (k - path.size()) + 1就可以了。
代码:
未剪枝优化
class Solution:def combinationSum3(self, k: int, n: int) -> List[List[int]]:result = [] # 初始化结果列表,用于存储所有满足条件的组合path = [] # 初始化当前组合路径列表,用于存储当前正在构建的组合self.backtracking(n, k, 0, 1, path, result) # 调用回溯方法开始搜索return result # 返回结果列表# 回溯方法,递归地搜索所有可能的组合def backtracking(self, targetSum, k, currentSum, startIndex, path, result):if len(path) == k: # 如果当前组合路径的长度等于k,说明已经找到了一个长度为k的组合if currentSum == targetSum: # 检查当前组合的和是否等于目标整数nresult.append(path[:]) # 如果等于,则将当前组合添加到结果列表中。注意:这里使用path[:]而不是path,是为了创建一个新的列表副本,避免后续修改影响结果return # 无论是否满足条件,都返回,结束当前递归分支for i in range(startIndex, 9+1): # 从startIndex开始遍历到9(包括9),因为题目要求组合中的整数范围是1到9 currentSum += i # 将当前整数i添加到当前组合的和中path.append(i) # 将当前整数i添加到当前组合路径中self.backtracking(targetSum, k, currentSum, i + 1, path, result) # 递归调用backtracking方法,继续搜索下一个整数。更新startIndex为i+1,确保不会重复使用相同的整数 # 回溯:撤销当前整数i的选择,以便尝试其他可能的整数currentSum -= i # 从当前组合的和中减去整数ipath.pop() # 从当前组合路径中移除整数i时间复杂度:分析回溯问题的时间复杂度,有一个通用公式:路径长度×搜索树的叶子数。对于本题,它等于 O(k⋅C(9,k))
空间复杂度:O(k)
剪枝优化
class Solution:def combinationSum3(self, k: int, n: int) -> List[List[int]]:result = []path = []self.backtracking(n, k, 0, 1, path, result)return resultdef backtracking(self, targetSum, k, currentSum, startIndex, path, result):if currentSum > targetSum: # 剪枝操作return if len(path) == k:if currentSum == targetSum:result.append(path[:])for i in range(startIndex, 9 + 1 - (k - len(path)) + 1 ): # 剪枝操作currentSum += ipath.append(i) self.backtracking(targetSum, k, currentSum, i + 1, path, result)currentSum -= ipath.pop()17. 电话号码的字母组合
思路:
从示例上来说,输入"23",最直接的想法就是两层for循环遍历了吧,正好把组合的情况都输出了。
如果输入"233"呢,那么就三层for循环,如果"2333"呢,就四层for循环.......
大家应该感觉出和77.组合 (opens new window)遇到的一样的问题,就是这for循环的层数如何写出来,此时又是回溯法登场的时候了。
例如:输入:"23",抽象为树形结构,如图所示:

图中可以看出遍历的深度,就是输入"23"的长度,而叶子节点就是我们要收集的结果,输出["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"]。
接着就是回溯三部曲:
- 确定回溯函数参数
- 确定终止条件
- 确定单层遍历逻辑
代码:
class Solution:def __init__(self):self.letterMap = ["", # 0"", # 1"abc", # 2"def", # 3"ghi", # 4"jkl", # 5"mno", # 6"pqrs", # 7"tuv", # 8"wxyz" # 9] # 创建一个映射表,将数字映射到一组字母self.result = [] # 初始化一个空的结果列表,用于存储所有可能的字母组合self.s = "" # 初始化一个空字符串,用于构建当前的字母组合def letterCombinations(self, digits: str) -> List[str]:if len(digits) == 0: # 如果输入的数字字符串为空,则直接返回空的结果列表return self.resultself.backtracking(digits, 0) # 调用回溯方法开始搜索所有可能的字母组合 return self.result # 返回结果列表# 回溯方法,用于搜索所有可能的字母组合def backtracking(self, digits, index):if index == len(digits): # 如果index等于digits的长度,说明已经处理完所有的数字self.result.append(self.s) # 将当前构建的字符串s添加到结果列表中return # 递归结束,返回digit = int(digits[index]) # 将索引处的数字转换为整数letters = self.letterMap[digit] # 获取当前处理的数字对应的字母组for i in range(len(letters)): # 遍历当前数字对应的每个字母self.s += letters[i] # 将当前字母添加到s中self.backtracking(digits, index + 1) # 递归处理下一个数字self.s = self.s[:-1] # 回溯,撤销之前的选择,即将当前的字母组合s中的最后一个字符删除 - 时间复杂度: O(3^m * 4^n),其中 m 是对应四个字母的数字个数,n 是对应三个字母的数字个数
- 空间复杂度: O(3^m * 4^n)