在深入探讨机器学习的核心概念之前，我们首先需要理解机器学习在当今世界的作用。机器学习，作为人工智能的一个重要分支，已经渗透到我们生活的方方面面，从智能推荐系统到自动驾驶汽车，再到医学影像的分析。它能够从大量数据中学习模式和规律，然后使用这些学习到的信息来做出预测或决策。本文将深入解析几个机器学习中的关键概念，包括逻辑回归、Softmax函数、均方误差(MSE)、交叉熵误差以及偏置项，并探讨它们在现实世界应用中的重要性。

一、逻辑回归：分类问题的利器

逻辑回归通常被用于二分类问题，是一种监督学习算法。不同于线性回归直接预测数值，逻辑回归通过Sigmoid函数将预测值压缩至0和1之间，表示为事件发生的概率。这个特性使得逻辑回归非常适用于需要概率解释的场景，比如电子邮件是否为垃圾邮件的分类、患者是否患有某种疾病的诊断等。

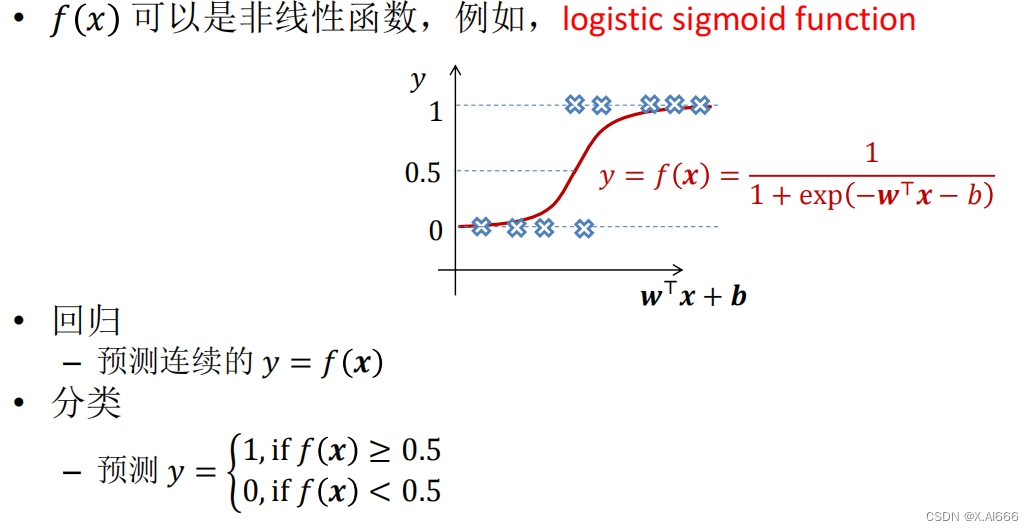
Sigmoid函数的魔力

Sigmoid函数是逻辑回归中的核心，这个函数将任何实数值映射到(0,1)区间内，使其可以解释为概率。它的S形曲线（或称为“逻辑曲线”）有一个显著的特性：当输入远离0时，输出迅速接近1或0，这对于清晰地划分不同类别极为有用。

二、Softmax函数：多分类问题的解决方案

当我们面对的是多于两个类别的分类问题时，Softmax函数就显得尤为重要。它可以被看作是Sigmoid函数在多类别情形下的推广。Softmax函数能够将一个K维的线性函数输出转换为一个概率分布，其中每一个输出代表着属于某一类别的概率。

Softmax的工作原理

给定一个对象的特征向量，Softmax模型首先计算每一个类别的得分（通常是通过线性函数），然后利用Softmax函数将这些得分转换为概率。这种机制允许模型在面对多分类问题时，能够给出每个类别的概率预测。

三、损失函数：衡量模型性能的关键

均方误差(MSE)：回归问题的标准

MSE是衡量模型预测值与实际值差异的常用方法，特别是在回归问题中。它计算了预测值与实际值之差的平方的平均值，公式为：MSE = \frac{1}{n}\sum_{i=1}^{n}(y_i - \hat{y_i})^2MSE=n1​∑i=1n​(yi​−yi​^​)2，其中y_iyi​是真实值，\hat{y_i}yi​^​是预测值。MSE的一个重要性质是，

它对较大的误差给予了更高的惩罚，这意味着模型预测中的大偏差将会导致损失函数值显著增加。这有助于引导模型更准确地拟合数据，但同时也意味着模型可能会对异常值过于敏感。

交叉熵误差：分类问题的选择

与MSE主要用于回归问题不同，交叉熵误差（Cross-Entropy Error）常用于分类问题，尤其是在输出层使用了Sigmoid或Softmax激活函数的神经网络模型中。交叉熵损失衡量的是实际输出分布和预测输出分布之间的差异。对于多分类问题，则使用Softmax输出的交叉熵公式。

交叉熵损失的一个关键优点是，在模型输出概率接近真实标签时，损失会逐渐减小，使得模型优化更为高效，尤其是在处理概率问题时更为适用。

四、偏置项：模型偏好的调整器

偏置项在机器学习模型中的作用不容小觑。它允许模型输出不完全依赖于输入特征的加权和，从而增加了模型的灵活性。简单来说，偏置项使得模型的决策边界可以沿着特征空间自由移动，而不是仅仅通过原点。这使得模型能够更好地适应数据，提高了模型的拟合能力和预测准确性。

在线性模型中，偏置项直接加在所有特征加权和之上，形式为：y = w_1x_1 + w_2x_2 + \dots + w_nx_n + by=w1​x1​+w2​x2​+⋯+wn​xn​+b，其中bb就是偏置项。在神经网络中，每个神经元都会有其对应的偏置项，起到调整激活函数输出的作用，从而影响网络的整体学习和预测表现。

结语

通过深入探讨逻辑回归、Softmax函数、MSE、交叉熵以及偏置项等机器学习核心概念，我们可以看到它们在模型构建和优化过程中的重要性。理解这些概念不仅有助于我们设计出更有效的模型来解决实际问题，而且也是深入学习更复杂机器学习算法和模型的基础。随着技术的不断进步，对这些基础知识的深入理解将使我们更好地掌握人工智能领域的未来发展。