目录
一,任意点到平移坐标轴面的投影
1,求解目标
2,转换变量
3,求解结果
4,f(t)的导数
5,f(t)的最小值
二,任意点到标准单纯形的投影
1,求解目标
2,公式变形
3,Moreau 分解
4,π函数的共轭函数
5,求解
6,总结
7,c++实现
本文来自论文:Projection Onto A Simplex
一,任意点到平移坐标轴面的投影
1,求解目标
求:

几何意义就是,考虑平移坐标轴面:

求任意一点y到这个平移坐标轴面的投影z,有了z就能求出整个式子的值了。
以n=2为例:

黑色线即坐标轴,红色线即平移坐标轴面,蓝色线展示了3个不同的投影例子。
2,转换变量
在几何意义中,我们当t是常数,对于任意点y,求y的投影点z。
反过来,我们把y当常数,即固定点,对于坐标轴面平移到不同的位置,即不同的t,有不同的投影点z。
3,求解结果
不防设y的n个分量是依次递增的,y1<=...<=yn,(全文同)
那么上式的结果就是:

其中,,
4,f(t)的导数
f(t)在全体实数域上是可导的

5,f(t)的最小值
f(t)的最小值一定是在导数为0的点,且一定存在唯一的点。
当时,f(t)取到最小值。
其中,
二,任意点到标准单纯形的投影
1,求解目标
标准单纯形: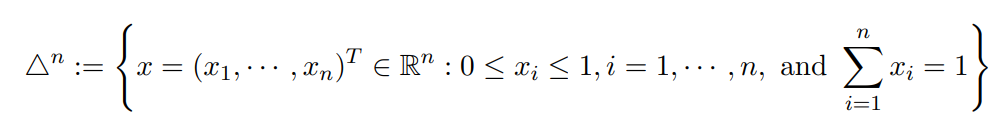
对于任意点y,求投影:

2,公式变形
定义函数:

那么求解目标转化成:
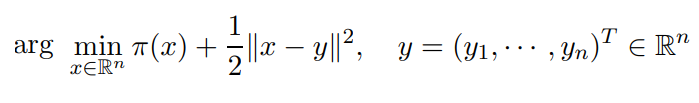
3,Moreau 分解
参考原函数的近端映射函数和共轭函数的近端映射函数的对偶
![]()
即:

所以只需要求出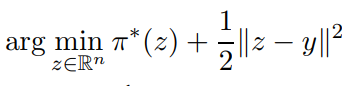
那么也就求出了
4,π函数的共轭函数

5,求解

其中,
所以,取,其中,
再取,
得到的就是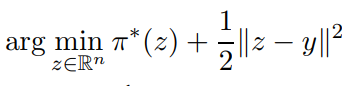
6,总结
不防设y1<=...<=yn
则求

只需要2步:
(1)取唯一的,其中,
(2)
7,c++实现
class VectorOpt
{
public://拓展数据域,加上idtemplate<typename T>static inline vector<pair<T, int>>expandWithId(const vector<T>& v){vector<pair<T, int>>ans;ans.resize(v.size());for (int i = 0; i < v.size(); i++)ans[i].first = v[i], ans[i].second = i;return ans;}//给vector拓展,加上id,但只按照原数据进行排序template<typename T>static inline vector<pair<T, int>> sortWithOrderMatch(const vector<T>& v){vector<pair<T, int>>ans = expandWithId(v);sort(ans.begin(), ans.end(), cmpJustFirst<T, int>);return ans;}
private:template<typename T>static inline bool cmp(T a, T b){return a < b;}template<typename T, typename T2>static inline bool cmpJustFirst(pair<T, T2> x, pair<T, T2> y){return cmp(x.first, y.first);}
};template<typename T>
vector<T> Simplexprojection(const vector<T> &x) //计算向量x到标准单纯形的投影
{vector<pair<T, int>> vp = VectorOpt::sortWithOrderMatch(x);int n = vp.size();T s = 0;for (int i = n - 1; i >= 0; i--) {s += vp[i].first;T t = (s - 1) / (n - i);if (i == 0 || t >= vp[i - 1].first) {vector<T> ans(vp.size());for (int i = n - 1; i >= 0; i--) {ans[vp[i].second] = max(vp[i].first - t, T{ 0 });}return ans;}}return x;
}