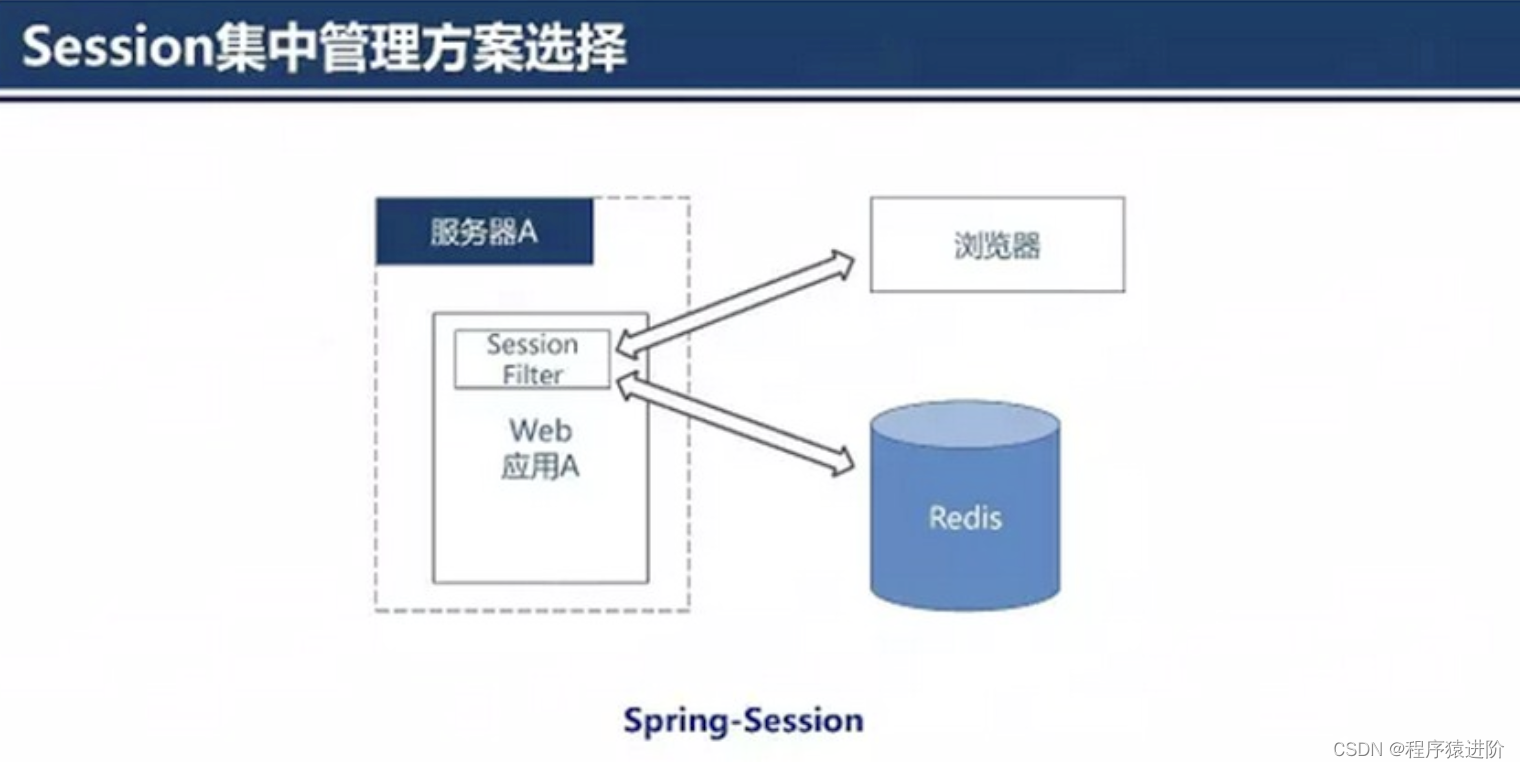
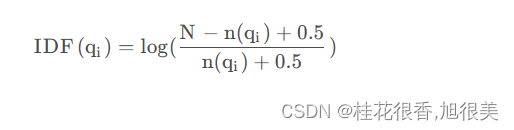最近和小伙伴聊到了一个问题：斜齿轮螺旋角和导程的关系，主要是在遇到在采用转位设计方式的刀具时，更觉得有点迷惑，今天咱们就聊聊这个事儿。

先来说斜齿轮螺旋角和导程的关系：

斜齿轮是有多个螺旋面组成的，其实就是端面的【渐开线齿廓】上的每一个点沿着齿轮的轴线做螺旋运动（一边沿着轴向平移，一边绕着轴线旋转），如下图所示：

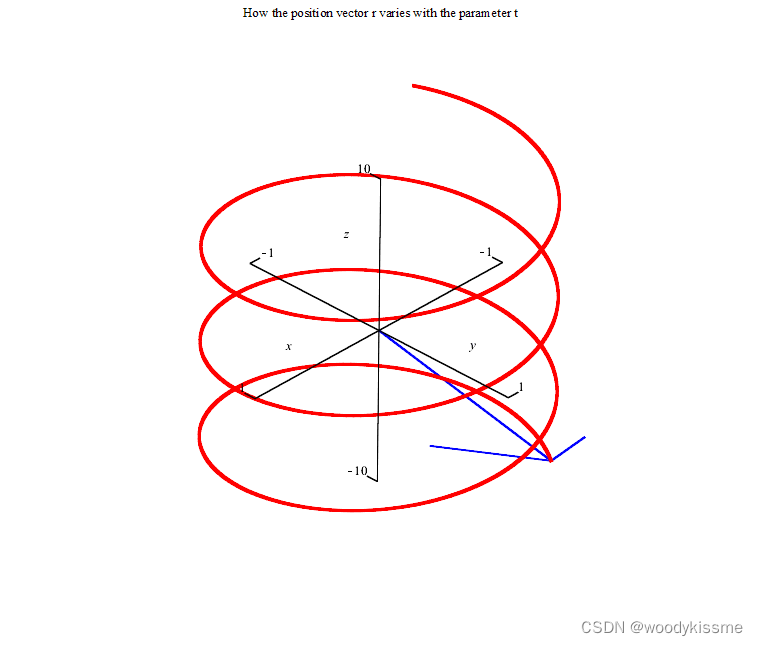
换成小球就更好理解了。

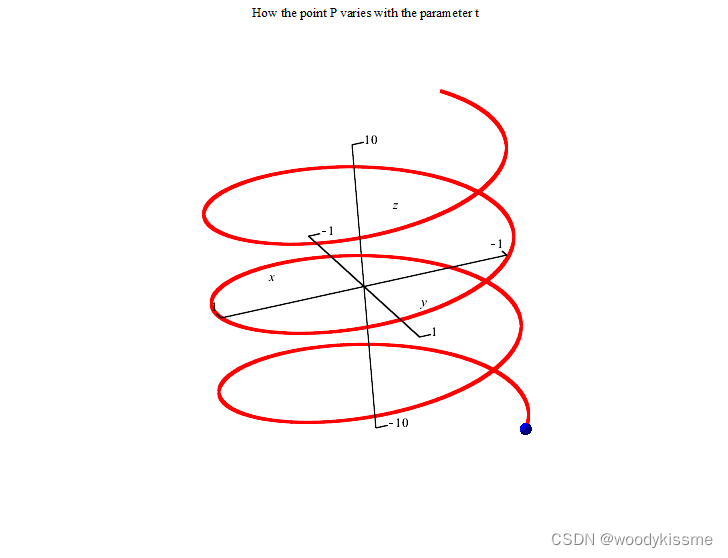
很多个点就形成了面：

下面是一个斜齿轮，分别画了三条螺旋线：齿顶、分度圆及齿根。

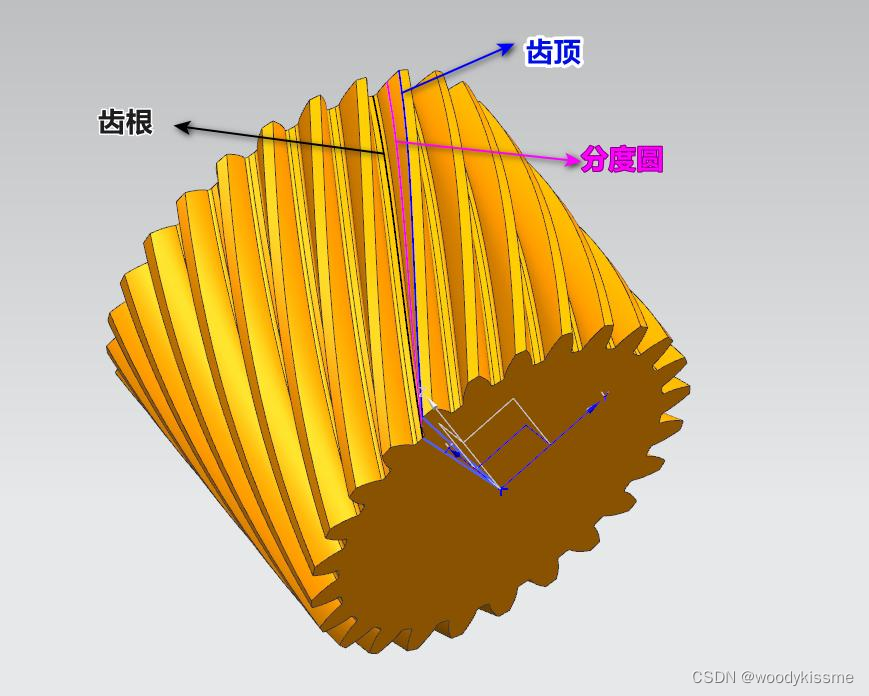
将齿轮的圆柱面展开来，就得到了下面这样咱们经常见到的图形，准确的说是一个直角三角形，两条直角边分别是齿轮端面的圆周长和导程，导程是螺旋线旋转一周后，沿旋转中心轴向方向所移动的距离。

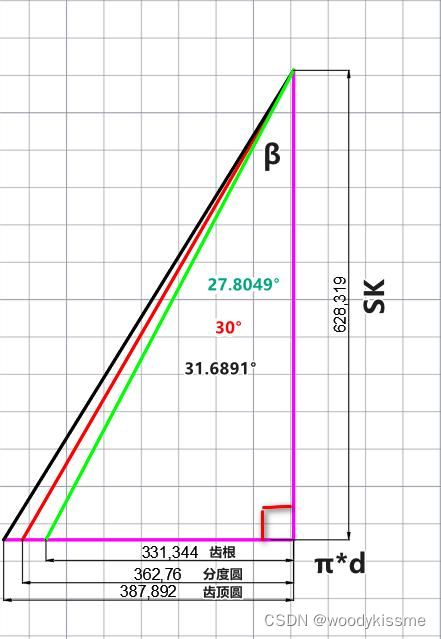
上图中的三条斜边分别是齿顶（黑色），分度圆（红色），齿根（绿色）上的螺旋线。由图可知：

SK=π*d/tan(β）

从公式和图我们可以看到，普通的圆柱齿轮是等导程的，也就是说齿面上的每一个点对应的螺旋线的导程都相等，从齿根到齿顶对应的螺旋角逐渐增大。前面咱们提过有非对称的齿轮，它也不例外，也是等导程的。

下面说说第二个问题，转位设计，俗称“变压力角”，其实我觉得应该叫“变分度圆”更为贴切，为什么呢？

我们知道渐开线从基圆开始，随着所在圆直径的增大，对应的压力角逐渐增大，可以看看这篇《》。齿轮的分度圆是一个人为规定的圆，既然是人为规定的，那它就是可以改变的，重新选取一个圆作为分度圆，此时它对应的模数和压力角以及螺旋角自然也跟着更改了，那和原理的分度圆上的模数、压力角及螺旋角有什么关系呢，看看下面这张图就清楚了：

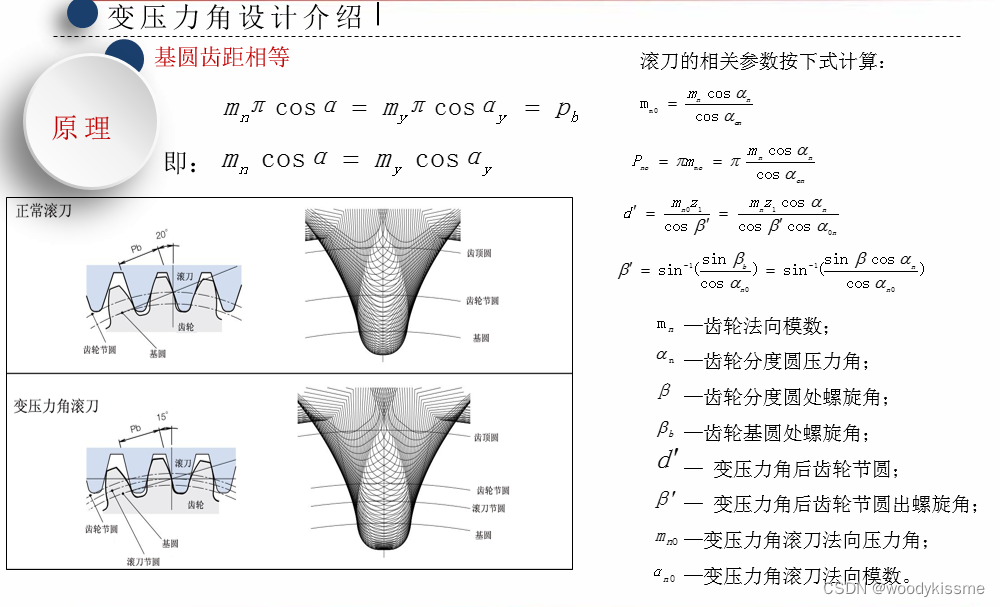
书上给的原理叫“基节”相等原理，因为渐开线的基圆是一个计算出的量，不随我们选取的分度圆的改变而变化。

至于为什么要采用转位设计，这个之前的文章也有介绍，这里就不再赘述啦。说了这么多和前面联系起来，如果压力角改变了，应为导程相等，所以对应的螺旋角也应随之改变。

我是woodykissme，定期分享有关，机械传动及齿轮加工方面的内容，对这方面感兴趣的小伙伴，可以关注我。希望能够与大家讨论一下：

齿轮的设计及加工方法，加工齿轮所用的刀具设计、制造及使用方面的相关问题。

齿轮刀具设计计算方法，相关应用程序的开发，CAD二次开发自动绘图等的相关技术问题。

刀具应用方面，刀具的切削参数、涂层和使用寿命，加工中遇到的问题和解决办法等问题。

今天就分享到这，感谢您抽出宝贵的时间阅读！