机器学习理论基础—集成学习

个体与集成

集成学习通过构建并结合多个学习器来完成学习任务，有时也称为多分类系统等。

分类： 根据集成学习中的个体学习器的不同可以分为同质集成（集成的学习器相同例如全部是决策树），和异质集成（集成的学习器包括多种，例如决策树神经网络SVM等）。

• 同质集成中的学习器称为：基学习器
• 异质集成中的学习器称为：组件学习器（或个体学习器）
• 弱学习器指的是泛化性能略优于随机猜想的学习器（例如二分类问题中精度略高于50%）

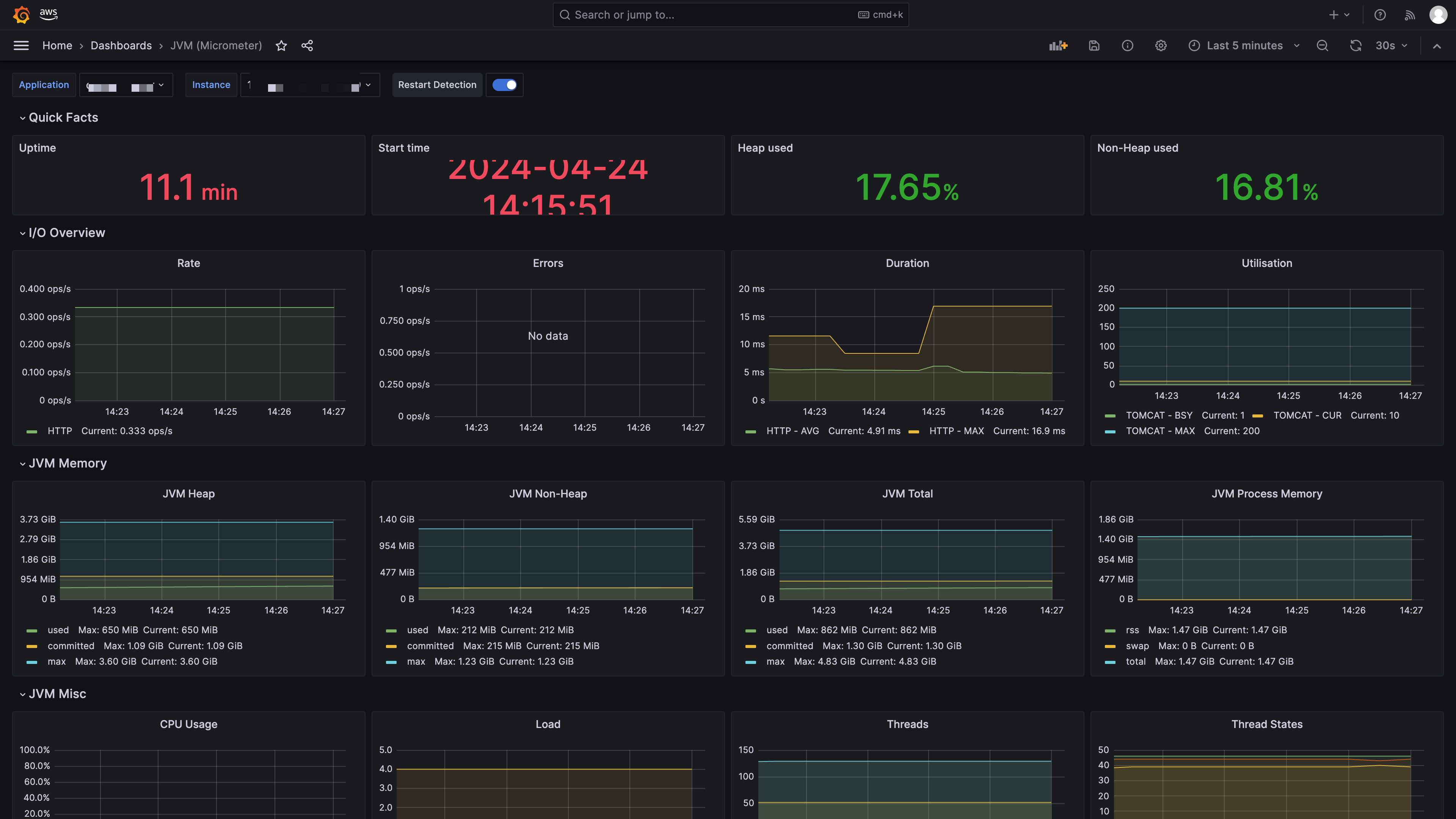
集成举例

样本一，样本二，样本三的label值都为1时（共三种情况）

首先集成学习的结果通过投票法产生，即少数服从多数的原则

1. 第一种情况：每个分类器都有66.6%的精度值经过集成学习之后提高了性能
2. 第二种情况：每个分类器都有33.3%的精度值经过集成学习之后结果变差了
3. 第三种情况：三个分类器没有差别集成的结果保持不变

总结： 集成学习器应该满足的两个基本条件是好而不同的。

集成个体学习器的收敛性保证

参数说明：

• F(x)集成了多个学习器的集成学习最后结果
• f(x)样本x的真实标签
• T个体学习器的数量
• &个体学习器的误差

解读：k个学习器成功预测样本x的概率

两个基本结论：

1. 收敛速率随着个体学习器数量T呈指数下降
2. ∈ =0.5的个体集成器对收敛没有作用

引入推导过程Hoeffing不等式（霍夫丁不等式）

分类

根据个体学习器的生成方式的不同分为两大类

1. 存在强依赖关系的（Boosting）
2. 不存在强的依赖关系的(随机森林)

2.2 算法原理

2.2.1 核心思想

需要解决的问题：

①在每一轮训练中，如何对训练样本的权值分布进行调整？

②如何确定各个基学习器“加权”结合的权重？

AdaBoost 的解决思路：

通过 分类器权重公式 来确定 各个基学习器的权重；通过 样本分布更新公式 来确定 各轮训练中的样本分布。

①在确定各个基学习器的权重时：

加大“分类误差率”小的弱分类器的权值，使其在表决中发挥较大作用；减小“分类误差率”大的弱分类器的权值，使其在表决中发挥较小作用。（直观而言：比较“菜”的学习器，权重应该小一些；比较“好”的学习器，权重应该大一些。）

②在确定各轮训练中的样本分布时：

提高那些被前一轮弱分类器错误分类样本的权值，降低那些被正确分类的样本的权值。（例如，假设我们在第 K 次得到的弱学习器，在某个样本上的分类结果出现错误，那么我们自然希望：第 K+1 次产生的弱学习器应该更加关注这个样本，使其尽可能地划分正确。）

2.2.2 分类情景介绍

下面我们从公式的角度推导 AdaBoost 的算法原理。为了防止公式混乱，我们给公式添加与《机器学习（周志华）》相同的编号；没有编号的公式是我们的推导过程。

AdaBoost 算法的训练目标是：基于“加性模型”，最小化指数损失函数。

注意，我们在这里讨论的是二分类问题，其中训练样本集的 y i ∈ { − 1 , + 1 } y_i\in\{-1,+1\} yi​∈{−1,+1} ，$f$ 是真实函数。对于样本 $x$ 来说，真实值 f ( x ) ∈ { − 1 , + 1 } f(x)\in\{-1,+1\} f(x)∈{−1,+1}，每个基学习器的预测值 h i ( x ) ∈ { − 1 , + 1 } h_i(x)\in\{-1,+1\} hi​(x)∈{−1,+1}，假定基分类器的错误率为 $ϵ$，即对每个基分类器 $h_i$ 有：
$$P(h_i(x)\ne f(x))=ϵ\text{\hspace{1em}(8.1)}$$
假设集成通过简单投票法结合 $T$ 个基分类器，若有超过半数的基分类器正确，则集成分类就正确；集成分类的结果 $F_{简单投票}(x)$ 为：
$$F_{简单投票}(x)=\mathrm{sign}(\sum _{i=1}^T{h}_i(x))\text{\hspace{1em}(8.2)}$$
“加性模型”（additive model），即基学习器的线性组合 $H(x)$：
$$H(x)=\sum _{t=1}^T{\alpha }_t{h}_t(x)\text{\hspace{1em}(8.4)}$$
其中，${\alpha }_t$ 表示基分类器的权重，因为 AdaBoost 并不使用简单投票法，而是“加权表决法”，即让基学习器具有不同的权值：
$$F(x)=\mathrm{sign}(H(x))=\mathrm{sign}(\sum _{t=1}^T{\alpha }_t{h}_t(x))$$
**“指数损失函数”**的定义为：
$$l_{exp}(H\mid D)={\mathbb{E}}_{x\sim D}[e^{-f(x)H(x)}]\text{\hspace{1em}(8.5)}$$
其中，$x\sim D$ 表示概率分布 $D(x)$，$\mathbb{E}$ 表示期望。

例如，下面的表格就列出了一个分布 $D(x)$：

序号 $i$	1	2	3	4	5	6	7	8	9	10
数据 $x$	0	1	2	3	4	5	6	7	8	9
类别标签 $y=f(x)$	1	1	1	-1	-1	-1	1	1	1	-1
权值分布 $D$	0.1	0.05	0.05	0.2	0.1	0.1	0.1	0.1	0.1	0.1

对于这里出现的“指数损失函数”，我们直观地理解一下使用它的合理性，随后在 2.2.2 节中说明使用它的正确性。

先考虑指数损失函数 $e^{-f(x)H(x)}$ 的含义：$f$ 为真实函数，对于样本 $x$ 来说， f ( x ) ∈ { − 1 , + 1 } f(x)\in\{-1,+1\} f(x)∈{−1,+1}，只能取 -1 和 +1，而 $H(x)$ 是一个实数，表示集成学习器的预测结果。当 $H(x)$ 的符号与 $f(x)$ 一致时，$f(x)H(x)>0$，因此，$e^{-f(x)H(x)}=e^{-|H(x)|}<1$，且 $|H(x)|$ 越大指数损失函数 $e^{-f(x)H(x)}$ 越小，（这很合理：此时 $|H(x)|$ 越大意味着分类器本身对预测结果的信心越大，损失应该越小；若 $|H(x)|$ 在零附近，虽然预测正确，但表示分类器本身对预测结果的信心很小，损失应该越大）；当 $H(x)$ 的符号与 $f(x)$ 不一致时，$f(x)H(x)<0$，因此，$e^{-f(x)H(x)}=e^{|H(x)|}>1$，且 $|H(x)|$ 越大，损失函数越大，（这很合理：因为此时 $|H(x)|$ 越大意味着分类器本身对预测结果的信心越大，但预测结果是错的，因此损失应该越大；若 $|H(x)|$ 在零附近，虽然预测错误，但表示分类器本身对预测结果的信心很小，虽然错了，损失应该很小）。

同时，我们不难得到两个工具公式（注意 $f(x)$ 是真实函数，也就是上表中 $x$ 所对应的 $y$ 的值）：
$${\mathbb{E}}_{x\sim D}[f(x)]=\sum _{x\in D}D(x)f(x)\text{\hspace{1em}(工具公式1)}$$

$$\sum _{i=1}^{|D|}D(x_i)\mathbb{I}(f(x_i)=1)=P(f(x_i)=1\mid x_i)\text{\hspace{1em}(工具公式2)}$$

这里我们引入“指示函数”的概念，$\mathbb{I}(\cdot )=\{\begin{array}{l}1;\cdot 为真\\ 0;\cdot 为假\end{array}$

2.2.3 使用“指数损失函数”的正确性

下面，我们从数学角度说明使用“指数损失函数”的正确性。

若集成学习器 $H(x)$ 能令指数损失函数最小化，则考虑式（8.5）对 $H(x)$ 的偏导：
$$\frac{\partial l_{exp}(H\mid D)}{\partial H(x)}=-e^{-H(x)}P(f(x)=1\mid x)+e^{H(x)}P(f(x)=-1\mid x)\text{\hspace{1em}(8.6)}$$

式（8.6）的具体推导过程为：

将工具公式1代入式（8.5）：
$$l_{exp}(H\mid D)={\mathbb{E}}_{x\sim D}[e^{-f(x)H(x)}]=\sum _{x\in D}D(x)e^{-f(x)H(x)}$$
由于工具公式2：
$$\sum _{i=1}^{|D|}D(x_i)\mathbb{I}(f(x_i)=1)=P(f(x_i)=1\mid x_i)$$
又注意到 f ( x i ) ∈ { − 1 , + 1 } f(x_i)\in\{-1,+1\} f(xi​)∈{−1,+1}，所以：
$$\begin{array}{rlr}\frac{\partial l_{exp}(H\mid D)}{\partial H(x)}& =\sum _{i=1}^{|D|}D(x_i)(-e^{-H(x_i)}\mathbb{I}(f(x_i)=1)+e^{H(x_i)}\mathbb{I}(f(x_i)=-1))& 分类讨论(两种情形)\\ & =-e^{-H(x_i)}P(f(x_i)=1\mid x_i)+e^{H(x_i)}P(f(x_i)=-1\mid x_i)& 由工具公式2得到\end{array}$$
式（8.6）的具体推导过程至此结束。

令式（8.6）为零，进行求解：
$$-e^{-H(x)}P(f(x)=1\mid x)+e^{H(x)}P(f(x)=-1\mid x)=0$$

$$H(x)+\ln (P(f(x)=-1\mid x))=-H(x)+\ln (P(f(x)=1\mid x))$$

可解得：
$$H(x)=\frac{1}{2}\ln \frac{P(f(x)=1\mid x)}{P(f(x)=-1\mid x)}\text{\hspace{1em}(8.7)}$$
因此，有：
s i g n ( H ( x ) ) = s i g n ( 1 2 l n P ( f ( x ) = 1 ∣ x ) P ( f ( x ) = − 1 ∣ x ) ) = { 1 , P ( f ( x ) = 1 ∣ x ) > P ( f ( x ) = − 1 ∣ x ) − 1 , P ( f ( x ) = 1 ∣ x ) < P ( f ( x ) = − 1 ∣ x ) 这三行表达的是一个意思 = a r g m a x y ∈ { − 1 , 1 } P ( f ( x ) = y ∣ x ) (8.8) \begin{aligned} \mathrm{sign}(H(x))&=\mathrm{sign}\Big(\dfrac{1}{2}\mathrm{ln}\dfrac{P(f(x)=1\mid x)}{P(f(x)=-1\mid x)}\Big)\\ &=\begin{cases}{1},&{P(f(x)=1\mid x)\gt P(f(x)=-1\mid x)}\\{-1},&{P(f(x)=1\mid x)\lt P(f(x)=-1\mid x)}\end{cases}&这三行表达的是一个意思\\ &=\mathop {\mathrm{argmax}}\limits_{y\in\{-1,1\}}P(f(x)=y\mid x) \end{aligned} \tag{8.8} sign(H(x))​=sign(21​lnP(f(x)=−1∣x)P(f(x)=1∣x)​)={1,−1,​P(f(x)=1∣x)>P(f(x)=−1∣x)P(f(x)=1∣x)<P(f(x)=−1∣x)​=y∈{−1,1}argmax​P(f(x)=y∣x)​这三行表达的是一个意思​(8.8)
这意味着 $\mathrm{sign}(H(x))$ 达到了贝叶斯最优错误率（即对于每个样本 $x$ 都选择后验概率最大的类别）。换言之，若指数损失函数最小化，则分类错误率也将最小化；这说明指数损失函数是分类任务原本 0/1 损失函数的一致的（consistent）替代损失函数。由于这个替代损失函数有更好的数学性质，例如它是连续可微函数，因此我们用它替代 0/1 损失函数作为优化目标。

至此，我们知道了使用“指数损失函数”的原因及其正确性。

2.2.4 分类器权重公式

下面，我们将从指数损失函数入手，推导 AdaBoost 算法的分类器权重公式。

在 AdaBoost 算法中，第一个基分类器 $h_1$ 是通过直接将基学习器算法用于初始数据分布而得；此后迭代地生成 $h_t$ 和 ${\alpha }_t$，当基分类器 $h_t$ 基于分布 $D_t$ 产生后，该基分类器的权重 ${\alpha }_t$ 应使得 ${\alpha }_t{h}_t$ 最小化指数损失函数。

此时的指数损失函数：
$$\begin{array}{rlr}{l}_{exp}({\alpha }_t{h}_t\mid D_t)& ={\mathbb{E}}_{x\sim D_t}[e^{-f(x){\alpha }_t{h}_t(x)}]& 由定义式(8.5)得到\\ & ={\mathbb{E}}_{x\sim D_t}[e^{-{\alpha }_t}\mathbb{I}(f(x)=h_t(x))+e^{{\alpha }_t}\mathbb{I}(f(x)\ne h_t(x))]& 分类讨论(两种情形)\\ & =\sum _{x\in D_t}{D}_t(x)[e^{-{\alpha }_t}\mathbb{I}(f(x)=h_t(x))+e^{{\alpha }_t}\mathbb{I}(f(x)\ne h_t(x))]& 由工具公式1得到\\ & =e^{-{\alpha }_t}{P}_{x\sim D_t}(f(x)=h_t(x))+e^{{\alpha }_t}{P}_{x\sim D_t}(f(x)\ne h_t(x))& 由工具公式2得到\\ & =e^{-{\alpha }_t}(1-{ϵ}_t)+e^{{\alpha }_t}{ϵ}_t& 错误率的定义\end{array}\text{\hspace{1em}(8.9)}$$
其中，错误率 ${ϵ}_t=P_{x\sim D_t}(h_t(x)\ne f(x))$。

考虑指数损失函数的导数：
$$\begin{array}{rlr}& \frac{\partial l_{exp}({\alpha }_t{h}_t\mid D_t)}{\partial {\alpha }_t}=-e^{-{\alpha }_t}(1-{ϵ}_t)+e^{{\alpha }_t}{ϵ}_t& 由式(8.9)对{\alpha }_t求偏导\end{array}\text{\hspace{1em}(8.10)}$$
令式（8.10）为零，进行求解：
$$\begin{array}{rlr}& -e^{-{\alpha }_t}(1-{ϵ}_t)+e^{{\alpha }_t}{ϵ}_t=0& 令式(8.10)为零\\ & & \\ & {\alpha }_t+\ln {ϵ}_t=-{\alpha }_t+\ln (1-{ϵ}_t)& 移项后取对数\end{array}$$

可解得：
$${\alpha }_t=\frac{1}{2}\ln \left(\frac{1-{ϵ}_t}{{ϵ}_t}\right)\text{\hspace{1em}(8.11)}$$
至此，我们求得了 AdaBoost 算法的分类器权重公式。

2.2.5 样本分布更新公式

下面，我们推导 AdaBoost 算法的样本分布更新公式。

AdaBoost 算法在获得 $H_{t-1}$ 之后样本分布将进行调整，使下一轮的基学习器 $h_t$ 能纠正 $H_{t-1}$ 的一些错误。

理想的 $h_t$ 能纠正 $H_{t-1}$ 的全部错误，又因为 $H(x)=H_{t-1}(x)+{\alpha }_t{h}_t(x)$。

因此，我们希望最小化 $l_{exp}(H_{t-1}+{\alpha }_t{h}_t\mid D)$，可以简化为，最小化：
$$\begin{array}{rl}{l}_{exp}(H_{t-1}+h_t\mid D)& ={\mathbb{E}}_{x\sim D}[e^{-f(x)(H_{t-1}(x)+h_t(x))}]\\ & ={\mathbb{E}}_{x\sim D}[e^{-f(x)H_{t-1}(x)}{e}^{-f(x)h_t(x)}]\end{array}\text{\hspace{1em}(8.12)}$$
对式（8.12）使用 $e^{-f(x)h_t(x)}$ 的泰勒展式近似：

使用到的泰勒展开式：$e^x\sim 1+x+\frac{1}{2}{x}^2+o(x^2)$

可得：
$$l_{exp}(H_{t-1}+h_t\mid D)\simeq {\mathbb{E}}_{x\sim D}\left[e^{-f(x)H_{t-1}(x)}\right(1-f(x)h_t(x)+\frac{f^2(x)h_t^2(x)}{2}\left)\right]$$
又因为 $f^2(x)=h_t^2(x)=1$，可得：
$$l_{exp}(H_{t-1}+h_t\mid D)={\mathbb{E}}_{x\sim D}\left[e^{-f(x)H_{t-1}(x)}\right(1-f(x)h_t(x)+\frac{1}{2}\left)\right]\text{\hspace{1em}(8.13)}$$
因为理想的基学习器 $h_t(x)$ 要使得指数损失函数最小化，所以：
$$\begin{array}{rlr}{h}_t(x)& =\underset{h}{\mathrm{argmin}}{l}_{exp}(H_{t-1}+h\mid D)& \\ & =\underset{h}{\mathrm{argmin}}{\mathbb{E}}_{x\sim D}\left[e^{-f(x)H_{t-1}(x)}\right(1-f(x)h(x)+\frac{1}{2}\left)\right]& 由式(8.13)代入得到\\ & =\underset{h}{\mathrm{argmin}}{\mathbb{E}}_{x\sim D}\left[e^{-f(x)H_{t-1}(x)}\right(-f(x)h(x)\left)\right]& 常数1+\frac{1}{2}不影响结果\\ & =\underset{h}{\mathrm{argmax}}{\mathbb{E}}_{x\sim D}[e^{-f(x)H_{t-1}(x)}f(x)h(x)]& 去负号\mathrm{argmin}变\mathrm{argmax}\\ & =\underset{h}{\mathrm{argmax}}{\mathbb{E}}_{x\sim D}[\frac{e^{-f(x)H_{t-1}(x)}}{{\mathbb{E}}_{x\sim D}[e^{-f(x)H_{t-1}(x)}]}f(x)h(x)]& 新加入的常数不影响结果\end{array}\text{\hspace{1em}(8.14)}$$
注意，式（8.14）中的 ${\mathbb{E}}_{x\sim D}[e^{-f(x)H_{t-1}(x)}]$ 是一个常数，之所以添加此常数，是为了构造出下面的 $D_t$ 分布。

令 $D_t$ 表示一个分布：
$$D_t(x)=\frac{D(x)e^{-f(x)H_{t-1}(x)}}{{\mathbb{E}}_{x\sim D}[e^{-f(x)H_{t-1}(x)}]}\text{\hspace{1em}(8.15)}$$
根据数学期望的定义，再将式（8.15）代入式（8.14），则理想的基学习器 $h_t(x)$：
$$\begin{array}{rlr}{h}_t(x)& =\underset{h}{\mathrm{argmax}}{\mathbb{E}}_{x\sim D}[\frac{e^{-f(x)H_{t-1}(x)}}{{\mathbb{E}}_{x\sim D}[e^{-f(x)H_{t-1}(x)}]}f(x)h(x)]& 式(8.14)\\ & =\underset{h}{\mathrm{argmax}}\sum _{i=1}^{|D|}D(x_i)\left[\frac{e^{-f(x_i)H_{t-1}(x_i)}f(x_i)h(x_i)}{{\mathbb{E}}_{x\sim D}[e^{-f(x_i)H_{t-1}(x_i)}]}\right]& 数学期望的定义\\ & =\underset{h}{\mathrm{argmax}}\sum _{i=1}^{|D|}{D}_t(x_i)f(x_i)h(x_i)& 由式(8.15)代入得到\\ & =\underset{h}{\mathrm{argmax}}{\mathbb{E}}_{x\sim D_t}[f(x)h(x)]& \end{array}\text{\hspace{1em}(8.16)}$$
由于 f ( x ) , h ( x ) ∈ { − 1 , + 1 } f(x),h(x)\in\{-1,+1\} f(x),h(x)∈{−1,+1}，有：
$$f(x)h(x)=1-2\mathbb{I}(f(x)\ne h(x))\text{\hspace{1em}(8.17)}$$
则理想的基学习器 $h_t(x)$：
$$\begin{array}{rlr}{h}_t(x)& =\underset{h}{\mathrm{argmax}}{\mathbb{E}}_{x\sim D_t}[f(x)h(x)]& 式(8.16)\\ & =\underset{h}{\mathrm{argmax}}{\mathbb{E}}_{x\sim D_t}[1-2\mathbb{I}(f(x)\ne h(x))]& 由式(8.17)代入得到\\ & =\underset{h}{\mathrm{argmin}}{\mathbb{E}}_{x\sim D_t}[\mathbb{I}(f(x)\ne h(x))]& 去掉常数和负号\end{array}\text{\hspace{1em}(8.18)}$$
由此可见，理想的 $h_t(x)$ 将在分布 $D_t$ 下最小化分类误差。

因此，弱分类器将基于分布 $D_t$ 进行训练，且针对 $D_t$ 的分类误差应小于 0.5，这在一定程度上类似“残差逼近”的思想。

考虑到 $D_t$ 与 $D_{t+1}$ 的关系，有：
$$\begin{array}{rlr}{D}_{t+1}(x)& =\frac{D(x)e^{-f(x)H_t(x)}}{{\mathbb{E}}_{x\sim D}[e^{-f(x)H_t(x)}]}& 由式(8.15)可得\\ & =\frac{D(x)e^{-f(x)H_{t-1}(x)}{e}^{-f(x){\alpha }_t{h}_t(x)}}{{\mathbb{E}}_{x\sim D}[e^{-f(x)H_t(x)}]}& 将H_t(x)展开得到\\ & =D_t(x)e^{-f(x){\alpha }_t{h}_t(x)}\frac{{\mathbb{E}}_{x\sim D}[e^{-f(x)H_{t-1}(x)}]}{{\mathbb{E}}_{x\sim D}[e^{-f(x)H_t(x)}]}& 将式(8.15)代入，构造D_t(x)\end{array}\text{\hspace{1em}(8.19)}$$
至此，我们求得了 AdaBoost 算法的样本分布更新公式。

于是，由式（8.11）和（8.19）可见，我们从基于加性模型最小化指数损失函数的角度，推导出了 AdaBoost 算法。

2.3 算法流程

2.3.1 算法描述

AdaBoost 算法流程如下：
$$\begin{array}{rl}输入:& 训练集D=\{(x_1,y_1),(x_2,y_2),\dots ,(x_m,y_m)\};\\ & 基学习算法\mathfrak{L};\\ & 训练轮数T.\\ 过程:& \\ & 1:D_1(x)=\frac{1}{m}.\\ & 2:\mathbf{for}t=1,2,\dots ,T\mathbf{do}\\ & 3:h_t=\mathfrak{L}(D,D_t);\\ & 4:{ϵ}_t=P_{x\sim D_t}(h_t(x)\ne f(x));\\ & 5:\mathbf{if}ϵ>0.5\mathbf{then}\mathbf{break}\\ & 6:{\alpha }_t=\frac{1}{2}ln\left(\frac{1-{ϵ}_t}{{ϵ}_t}\right);\\ & 7:D_{t+1}(x)=\frac{D_t(x)}{Z_t}\times \{\begin{array}{ll}{e}^{-{\alpha }_t},& \mathrm{if}{h}_t(x)=f(x)\\ e^{{\alpha }_t},& \mathrm{if}{h}_t(x)\ne f(x)\end{array}=\frac{D_t(x)e^{-{\alpha }_{t}f(x)h_t(x)}}{Z_t}\\ & 8:\mathbf{end}\mathbf{for}\\ 输出:& F(x)=\mathrm{sign}(\sum _{t=1}^T{\alpha }_t{h}_t(x))\end{array}$$
其中，$Z_t$ 是规范化因子，它使得 $D_{t+1}$ 是一个分布：
$$Z_t=\sum _{i=1}^N{w}_{ti}{e}^{-{\alpha }_{t}f(x_i)h_t(x_i)}$$
我们知道，$D_{t+1}$ 表示的是样本权值的分布；因此，要想使得 $D_{t+1}$ 是一个分布，应当使得 $D_{t+1}$ 中的各样本权值之和为 1。为了做到这点，我们让 $D_{t+1}$ 中的每一个规范化前的样本权值 $w_{ti}{e}^{-{\alpha }_{t}f(x_i)h_t(x_i)}$ 都除以样本权值的总和 $\sum _{i=1}^N{w}_{ti}{e}^{-{\alpha }_{t}f(x_i)h_t(x_i)}$（这个总和也就是规范化因子 $Z_t$），从而让我们得到的各样本权值之和为 1。（直观来说，规范化后的样本权值，即为规范化前的样本权值 占 总样本权值的比例，这个比例的总和当然为 1。）

所以我们也能理解：在式（8.19）中，由于项 $\frac{{\mathbb{E}}_{x\sim D}[e^{-f(x)H_{t-1}(x)}]}{{\mathbb{E}}_{x\sim D}[e^{-f(x)H_t(x)}]}$ 是一个常数，所有样本权值同时乘以常数，不会改变规范化前的样本权值 占 总样本权值的比例；因此无论是否有它，规范化之后的结果都是一样的，所以我们不去计算这个常数的值。

2.3.2 算法各步骤含义

AdaBoost 算法各步骤的含义如下（一一对应）：
$$\begin{array}{rl}输入:& 训练集D=\{(x_1,y_1),(x_2,y_2),\dots ,(x_m,y_m)\};\\ & 基学习算法\mathfrak{L};\\ & 训练轮数T.\\ 过程:& \\ & 1:初始化样本权值分布.\\ & 2:循环进行T轮训练\\ & 3:基于分布D_t从数据集D中训练出分类器h_t;\\ & 4:估计h_t的误差;\\ & 5:检查当前基分类器是否比随机猜测好，如果条件不满足，当前基学习器即被抛弃，学习过程停止\\ & 6:确定分类器h_t的权重;\\ & 7:更新样本分布，其中Z_t是规范化因子，以确保D_{t+1}是一个分布\\ & 8:结束循环\\ 输出:& 分类结果\end{array}$$

2.4 具体算例

2.4.1 给定数据集与基学习算法

假设给出如下表所示的训练数据。假设弱分类器由 $x<v$ 或 $x>v$ 产生，其阈值 $v$ 使该分类器在训练数据集上的分类误差率最低。试用 AdaBoost 算法学习一个强分类器。

序号 $i$	1	2	3	4	5	6	7	8	9	10
数据 $x$	0	1	2	3	4	5	6	7	8	9
类别标签 $y=f(x)$	1	1	1	-1	-1	-1	1	1	1	-1

2.4.2 算法步骤1-2

解：

我们用 $t$ 表示当前训练的轮数， $i$ 表示实例的序号，$m$ 表示训练集实例的总数量。

在此例中，$t=1,2,\dots ,T$；$i=1,2,\dots ,10$；$m=10$。

1：初始化样本权值分布 $D_1(x)$：
$$D_1(x)=(w_{11},w_{12},\dots ,w_{110})=\frac{1}{m}$$

$$w_{1i}=0.1,i=1,2,\dots ,10$$

这里，$w_{ti}$ 表示第 $t$ 轮中第 $i$ 个实例的权值，并且 $\sum _{i=1}^N{w}_{ti}=1$。

2：开始循环进行 $T$ 轮训练：

其中，下面的序号 $a$ 表示第 1 轮训练，$b$ 表示第 2 轮训练，以此类推。

2.4.3 算法步骤3a-7a（第 1 轮）

3a：基于分布 $D_t=D_1$ 从数据集 $D$ 中训练出分类器 $h_t=h_1$：
$$h_1=\mathfrak{L}(D,D_1)$$
在权值分布为 $D_1$ 的训练数据上，阈值 $v$ 取 2.5 时分类误差率最低，故基本分类器为：
$$h_1(x)=\{\begin{array}{ll}1,& x<2.5\\ -1,& x>2.5\end{array}$$
4a：估计 $h_1$ 的误差：

序号 $i$	1	2	3	4	5	6	7	8	9	10
数据 $x$	0	1	2	3	4	5	6	7	8	9
类别标签 $y=f(x)$	1	1	1	-1	-1	-1	1	1	1	-1
权值分布 $D_1$	0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.1
基分类器结果 $h_1(x)$	1	1	1	-1	-1	-1	-1	-1	-1	-1
正误	√	√	√	√	√	√	×	×	×	√

$h_1(x)$ 的在训练数据集上的误差率为：
$${ϵ}_1=P_{x\sim D_1}(h_1(x)\ne f(x))=0.1+0.1+0.1=0.3$$
务必注意：模型的误差等于误判样本的权重值之和（可以看作弱学习器在数据集上的加权错误率），而非误判样本数占总样本数的比例。

5a：检查当前基分类器是否比随机猜测好：
$${ϵ}_1=0.3\le 0.5$$
基分类器 $h_1$ 比随机猜测好，循环继续进行。

6a：确定分类器 $h_t=h_1$ 的权重 ${\alpha }_1$：
$${\alpha }_1=\frac{1}{2}ln\left(\frac{1-{ϵ}_1}{{ϵ}_1}\right)=\frac{1}{2}ln\left(\frac{1-0.3}{0.3}\right)=0.4236$$
7a：更新样本的权值分布：
$$D_2=(w_{21},\dots ,w_{2i},\dots ,w_{210})=\frac{D_1(x)e^{-{\alpha }_{1}f(x)h_1(x)}}{Z_1}$$

$$w_{2i}=\frac{w_{1i}}{Z_1}{e}^{-{\alpha }_{1}f(x_i)h_1(x_i)},i=1,2,\dots ,10$$

且已求得，基分类器权重 ${\alpha }_1=0.4236$

可求，规范化因子（为了使样本的概率分布之和为1）：
$$Z_t=\sum _{i=1}^N{w}_{ti}{e}^{-{\alpha }_{t}f(x_i)h_t(x_i)}$$

$$\begin{array}{rl}{Z}_1& =\sum _{i=1}^N{w}_{1i}{e}^{-{\alpha }_{1}f(x_i)h_1(x_i)}\\ & =0.1e^{-0.4236}+0.1e^{-0.4236}+0.1e^{-0.4236}+0.1e^{-0.4236}+0.1e^{-0.4236}+0.1e^{-0.4236}+0.1e^{0.4236}+0.1e^{0.4236}+0.1e^{0.4236}+0.1e^{-0.4236}\\ & =0.1e^{-0.4236}\times 7+0.1e^{0.4236}\times 3简化计算\\ & =0.06546857\times 7+0.15274505\times 3\\ & =0.91651514\end{array}$$

可求得：

序号 $i$	1	2	3	4	5	6	7	8	9	10
数据 $x$	0	1	2	3	4	5	6	7	8	9
类别标签 $y=f(x)$	1	1	1	-1	-1	-1	1	1	1	-1
权值分布 $D_1=(w_{1i})$	0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.1	0.1
基分类器结果 $h_1(x)$	1	1	1	-1	-1	-1	-1	-1	-1	-1
分子${}^{[1]}$$w_{1i}{e}^{-{\alpha }_{1}f(x_i)h_1(x_i)}$	0.06546857	0.06546857	0.06546857	0.06546857	0.06546857	0.06546857	0.15274505	0.15274505	0.15274505	0.06546857
权值分布${}^{[2]}$ $D_2=(w_{2i})$	0.07143	0.07143	0.07143	0.07143	0.07143	0.07143	0.16666	0.16666	0.16666	0.07143

[1]这里的分子计算：$0.1e^{-0.4236}=0.06546857$；$0.1e^{0.4236}=0.15274505$

[2]可以观察到：第 1 轮中基学习器分类错误的样本 x=6,7,8，在 $D_2$ 中的权重变大了，而其他样本权重降低了。

此时的集成分类器：
$$H_1(x)=0.4236h_1(x)$$
分类结果 $F(x)=\mathrm{sign}(0.4236h_1(x))$ 在训练数据集上有 3 个误分类点。

2.4.4 算法步骤3b-7b（第 2 轮）

3b：基于分布 $D_t=D_2$ 从数据集 $D$ 中训练出分类器 $h_t=h_2$：
$$h_2=\mathfrak{L}(D,D_2)$$
在权值分布为 $D_2$ 的训练数据上，阈值 $v$ 取 8.5 时分类误差率最低，故基本分类器为：
$$h_2(x)=\{\begin{array}{ll}1,& x<8.5\\ -1,& x>8.5\end{array}$$
4b：估计 $h_2$ 的误差：

序号 $i$	1	2	3	4	5	6	7	8	9	10
数据 $x$	0	1	2	3	4	5	6	7	8	9
类别标签 $y=f(x)$	1	1	1	-1	-1	-1	1	1	1	-1
权值分布 $D_2$	0.07143	0.07143	0.07143	0.07143	0.07143	0.07143	0.16666	0.16666	0.16666	0.07143
基分类器结果 $h_2(x)$	1	1	1	1	1	1	1	1	1	-1
正误	√	√	√	×	×	×	√	√	√	√

$h_2(x)$ 的在训练数据集上的误差率为：
$${ϵ}_2=P_{x\sim D_2}(h_2(x)\ne f(x))=0.07143+0.07143+0.07143=0.2143$$
5b：检查当前基分类器是否比随机猜测好：
$${ϵ}_2=0.2143\le 0.5$$
基分类器 $h_2$ 比随机猜测好，循环继续进行。

6b：确定分类器 $h_t=h_2$ 的权重 ${\alpha }_2$：
$${\alpha }_2=\frac{1}{2}ln\left(\frac{1-{ϵ}_2}{{ϵ}_2}\right)=\frac{1}{2}ln\left(\frac{1-0.2143}{0.2143}\right)=0.6496$$
7b：更新样本的权值分布：
$$D_3=(w_{31},\dots ,w_{3i},\dots ,w_{310})=\frac{D_2(x)e^{-{\alpha }_{2}f(x)h_2(x)}}{Z_2}$$

$$w_{3i}=\frac{w_{2i}}{Z_2}{e}^{-{\alpha }_{2}f(x_i)h_2(x_i)},i=1,2,\dots ,10$$

且已求得，基分类器权重 ${\alpha }_2=0.6496$

可求，规范化因子：
$$Z_t=\sum _{i=1}^N{w}_{ti}{e}^{-{\alpha }_{t}f(x_i)h_t(x_i)}$$

$$\begin{array}{rl}{Z}_2& =\sum _{i=1}^N{w}_{2i}{e}^{-{\alpha }_{2}f(x_i)h_2(x_i)}\\ & =0.07143e^{-0.6496}+0.07143e^{-0.6496}+0.07143e^{-0.6496}+0.07143e^{0.6496}+0.07143e^{0.6496}+0.07143e^{0.6496}+0.16666e^{-0.6496}+0.16666e^{-0.6496}+0.16666e^{-0.6496}+0.07143e^{-0.6496}\\ & =0.07143e^{-0.6496}\times 4+0.07143e^{0.6496}\times 3+0.16666e^{-0.6496}\times 3简化计算\\ & =0.03730465\times 4+0.13677236\times 3+0.08703896\times 3\\ & =0.82065256\end{array}$$

可求得：

序号 $i$	1	2	3	4	5	6	7	8	9	10
数据 $x$	0	1	2	3	4	5	6	7	8	9
类别标签 $y=f(x)$	1	1	1	-1	-1	-1	1	1	1	-1
权值分布 $D_2=(w_{2i})$	0.07143	0.07143	0.07143	0.07143	0.07143	0.07143	0.16666	0.16666	0.16666	0.07143
基分类器结果 $h_2(x)$	1	1	1	1	1	1	1	1	1	-1
分子${}^{[3]}$ $w_{2i}{e}^{-{\alpha }_{2}f(x_i)h_2(x_i)}$	0.03730465	0.03730465	0.03730465	0.13677236	0.13677236	0.13677236	0.08703896	0.08703896	0.08703896	0.03730465
权值分布${}^{[4]}$ $D_3=(w_{3i})$	0.04546	0.04546	0.04546	0.16666	0.16666	0.16666	0.10606	0.10606	0.10606	0.04546

[3]这里的分子计算：$0.07143e^{-0.6496}=0.03730465$；$0.07143e^{0.6496}=0.13677236$；$0.16666e^{-0.6496}=0.08703896$

[4]可以观察到：第 2 轮中基学习器分类错误的样本 x=3,4,5，在 $D_3$ 中的权重变大了，而其他样本权重降低了。

此时的集成分类器：
$$H_2(x)=0.4236h_1(x)+0.6496h_2(x)$$
分类结果 $F(x)=\mathrm{sign}(0.4236h_1(x)+0.6496h_2(x))$ 在训练数据集上有 3 个误分类点。

2.4.5 算法步骤3c-7c（第 3 轮）

3c：基于分布 $D_t=D_3$ 从数据集 $D$ 中训练出分类器 $h_t=h_3$：
$$h_3=\mathfrak{L}(D,D_3)$$
在权值分布为 $D_3$ 的训练数据上，阈值 $v$ 取 5.5 时分类误差率最低，故基本分类器为：
$$h_3(x)=\{\begin{array}{ll}1,& x>5.5\\ -1,& x<5.5\end{array}$$
4c：估计 $h_3$ 的误差：

序号 $i$	1	2	3	4	5	6	7	8	9	10
数据 $x$	0	1	2	3	4	5	6	7	8	9
类别标签 $y=f(x)$	1	1	1	-1	-1	-1	1	1	1	-1
权值分布 $D_3$	0.04546	0.04546	0.04546	0.16666	0.16666	0.16666	0.10606	0.10606	0.10606	0.04546
基分类器结果 $h_3(x)$	-1	-1	-1	-1	-1	-1	1	1	1	1
正误	×	×	×	√	√	√	√	√	√	×

$h_3(x)$ 的在训练数据集上的误差率为：
$${ϵ}_3=P_{x\sim D_3}(h_3(x)\ne f(x))=0.04546+0.04546+0.04546+0.04546=0.1818$$
5c：检查当前基分类器是否比随机猜测好：
$${ϵ}_3=0.1818\le 0.5$$
基分类器 $h_3$ 比随机猜测好，循环继续进行.

6c：确定分类器 $h_t=h_3$ 的权重 ${\alpha }_3$：
$${\alpha }_3=\frac{1}{2}ln\left(\frac{1-{ϵ}_3}{{ϵ}_3}\right)=\frac{1}{2}ln\left(\frac{1-0.1818}{0.1818}\right)=0.7521$$
7c：更新样本的权值分布：
$$D_4=(w_{41},\dots ,w_{4i},\dots ,w_{410})=\frac{D_3(x)e^{-{\alpha }_{3}f(x)h_3(x)}}{Z_3}$$

$$w_{4i}=\frac{w_{3i}}{Z_3}{e}^{-{\alpha }_{3}f(x_i)h_3(x_i)},i=1,2,\dots ,10$$

且已求得，基分类器权重 ${\alpha }_3=0.7521$

可求，规范化因子：
$$Z_t=\sum _{i=1}^N{w}_{ti}{e}^{-{\alpha }_{t}f(x_i)h_t(x_i)}$$

$$\begin{array}{rl}{Z}_3& =\sum _{i=1}^N{w}_{3i}{e}^{-{\alpha }_{3}f(x_i)h_3(x_i)}\\ & =0.04546e^{0.7521}+0.04546e^{0.7521}+0.04546e^{0.7521}+0.16666e^{-0.7521}+0.16666e^{-0.7521}+0.16666e^{-0.7521}+0.10606e^{-0.7521}+0.10606e^{-0.7521}+0.10606e^{-0.7521}+0.04546e^{0.7521}\\ & =0.04546e^{0.7521}\times 4+0.16666e^{-0.7521}\times 3+0.10606e^{-0.7521}\times 3简化计算\\ & =0.09644113\times 4+0.07855946\times 3+0.04999410\times 3\\ & =0.77142520\end{array}$$

可求得：

序号 $i$	1	2	3	4	5	6	7	8	9	10
数据 $x$	0	1	2	3	4	5	6	7	8	9
类别标签 $y=f(x)$	1	1	1	-1	-1	-1	1	1	1	-1
权值分布 $D_3=(w_{3i})$	0.04546	0.04546	0.04546	0.16666	0.16666	0.16666	0.10606	0.10606	0.10606	0.04546
基分类器结果 $h_3(x)$	-1	-1	-1	-1	-1	-1	1	1	1	1
分子${}^{[5]}$ $w_{3i}{e}^{-{\alpha }_{3}f(x_i)h_3(x_i)}$	0.09644113	0.09644113	0.09644113	0.07855946	0.07855946	0.07855946	0.04999410	0.04999410	0.04999410	0.09644113
权值分布${}^{[6]}$ $D_4=(w_{4i})$	0.12502	0.12502	0.12502	0.10184	0.10184	0.10184	0.06481	0.06481	0.06481	0.12502

[5]这里的分子计算：$0.04546e^{0.7521}=0.09644113$；$0.16666e^{-0.7521}=0.07855946$；$0.10606e^{-0.7521}=0.04999410$

[6]可以观察到：第 3 轮中基学习器分类错误的样本 x=0,1,2,9，在 $D_4$ 中的权重变大了，而其他样本权重降低了。

此时的集成分类器：
$$H_3(x)=0.4236h_1(x)+0.6496h_2(x)+0.7521h_3(x)$$
分类结果 $F(x)=\mathrm{sign}(0.4236h_1(x)+0.6496h_2(x)+0.7521h_3(x))$ 在训练数据集上有 0 个误分类点。

具体如下：

序号 $i$	1	2	3	4	5	6	7	8	9	10
数据 $x$	0	1	2	3	4	5	6	7	8	9
类别标签 $y=f(x)$	1	1	1	-1	-1	-1	1	1	1	-1
基分类器结果 $h_1(x)$	1	1	1	-1	-1	-1	-1	-1	-1	-1
加权 ${\alpha }_1{h}_1(x)$	0.4236	0.4236	0.4236	-0.4236	-0.4236	-0.4236	-0.4236	-0.4236	-0.4236	-0.4236
基分类器结果 $h_2(x)$	1	1	1	1	1	1	1	1	1	-1
加权 ${\alpha }_2{h}_2(x)$	0.6496	0.6496	0.6496	0.6496	0.6496	0.6496	0.6496	0.6496	0.6496	-0.6496
基分类器结果 $h_3(x)$	-1	-1	-1	-1	-1	-1	1	1	1	1
加权 ${\alpha }_3{h}_3(x)$	-0.7521	-0.7521	-0.7521	-0.7521	-0.7521	-0.7521	0.7521	0.7521	0.7521	0.7521
$\sum _{t=1}^T{\alpha }_t{h}_t(x)$	0.3211	0.3211	0.3211	-0.5261	-0.5261	-0.5261	0.9781	0.9781	0.9781	-0.3211
集成分类器结果 $F(x)$	1	1	1	-1	-1	-1	1	1	1	-1
正误	√	√	√	√	√	√	√	√	√	√

2.4.6 算法步骤8

8：结束循环

输出结果：
$$F(x)=\mathrm{sign}(\sum _{t=1}^T{\alpha }_t{h}_t(x))=\mathrm{sign}(0.4236h_1(x)+0.6496h_2(x)+0.7521h_3(x))$$
AdaBoost 算法在本数据集的运算至此结束。

2.5 代码实现

见代码文件“AdaBoost.ipynb”。

2.6 算法分析

2.6.1 主要优点

①AdaBoost 作为分类器时，分类精度很高，训练误差以指数速率下降；

②在 AdaBoost 的框架下，可以使用各种回归分类模型来构建弱学习器，非常灵活；

③作为简单的二元分类器时，构造简单，结果可理解。

2.6.2 主要缺点

在 Adaboost 训练过程中，Adaboost 会使得难于分类的样本的权值呈指数增长，训练将会过于偏向这类困难的样本；因此它对异常样本是敏感的，异常样本在迭代中可能会获得较高的权重，影响最终强学习器的预测准确性。

2.7 常用技巧

2.7.1 特征缩减技术（Shrinkage）

对每个基学习器乘以一个系数 $v(0<v<1)$，使其对最终模型的贡献减小，从而防止学的太快产生过拟合，$v$ 又称学习率（learning rate）。

于是，上文的加法模型就从：
$$H(x)=H_{t-1}(x)+{\alpha }_t{h}_t(x)$$
变为：
$$H(x)=H_{t-1}(x)+v\cdot {\alpha }_t{h}_t(x)$$
一般 $v$ 要和迭代次数 $T$ 结合起来使用，较小的 $v$ 意味着需要较大的 $T$。

《The Elements of Staistical Learning》提到的策略是先将 $v$ 设得很小 $(v<0.1)$，再通过 Early Stopping 选择 $T$；现实中也常用交叉验证（cross-validation）进行选择。

2.7.2 早停法（Early Stopping）

将数据集划分为训练集和测试集，在训练过程中不断检查在测试集上的表现，如果测试集上的准确率下降到一定阈值之下，则停止训练，选用当前的迭代次数 $T$，这同样是防止过拟合的手段。

2.7.3 权值修整（Weight Trimming）

Weight Trimming 的主要目的是提高训练速度，且不显著牺牲准确率。

在 AdaBoost 的每一轮基学习器训练过程中，只有小部分样本的权重较大，因而能产生较大的影响；而其他大部分权重小的样本则对训练影响甚微。

Weight Trimming 的思想是每一轮迭代中删除那些低权重的样本，只用高权重样本进行训练。具体是设定一个阈值（比如90%或99%），再将所有样本按权重排序，计算权重的累积和，累积和大于阈值的权重 (样本) 被舍弃，不会用于训练。注意每一轮训练完成后所有样本的权重依然会被重新计算，这意味着之前被舍弃的样本在之后的迭代中如果权重增加，可能会重新用于训练。

参考文献[9]中有使用 Weight Trimming 的 AdaBoost 代码，可供参考。

2.8 参考文献

[1]《机器学习》周志华

[2]《统计学习方法》李航

[3]《机器学习西瓜书之集成学习》爱你的小魔仙 https://www.bilibili.com/video/BV1PK4y147VQ/

[4] 《集成学习 之【Adaboost】 —— 李航《统计学习方法》相关章节解读》老弓的学习日记 https://www.bilibili.com/video/BV1x44y1r7Zc

[5]《通俗易懂讲算法-Adaboost》青青草原灰太郎 https://www.bilibili.com/video/BV13S4y1t7aY/

[6]《Adaboost是如何训练弱分类器的》herain https://www.zhihu.com/question/443511497?utm_id=0

[7]《集成学习之Boosting —— AdaBoost原理》wdmad https://zhuanlan.zhihu.com/p/37358517

[8]《集成学习之Boosting —— AdaBoost实现》wdmad https://zhuanlan.zhihu.com/p/37357981

[9]《AdaBoost 算法》Rnan-prince https://blog.csdn.net/qq_19446965/article/details/104200720

[10]《集成学习（Ensemble learning）》张梓寒 https://www.cnblogs.com/ZihanZhang/p/16351469.html

[11]《Statistical-Learning-Method_Code》Dod-o https://github.com/Dod-o/Statistical-Learning-Method_Code