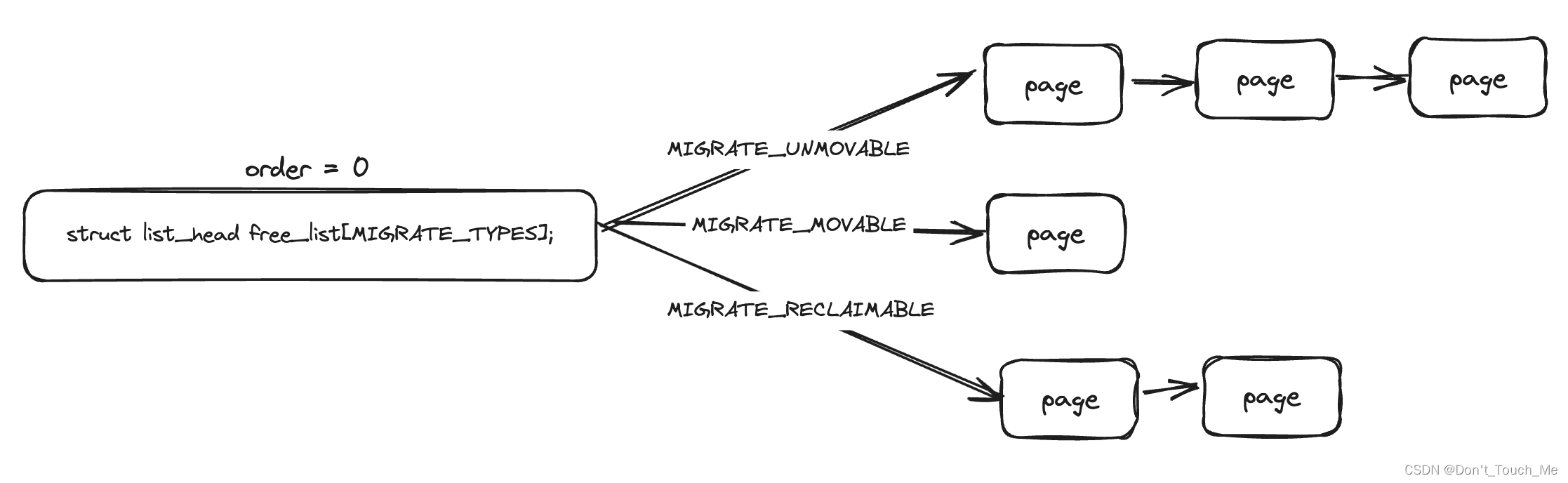
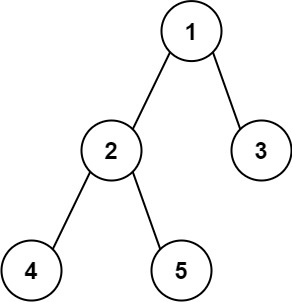
相比于定义一个循环双向链表来实现插入排序来说，下面的实现采用一个单向循环链表来实现，并且不需要定义一个单向循环链表类，而是把一个list（数组/顺序表）当成单向循环链表来用，list的元素是一个包含两个元素的对象，一个是数值，一个是指向下一个list元素的指针（list的元素下标），list的第一个元素（下标为0的元素）是单链表的头结点，它不存放数据，起到哨兵的作用。

        排序的时候，把一个数据元素插入一个位置，不需要移动数据，只需要修改该位置前一个list元素和待插入数据元素的指针域就行，其实就是个单向链表的插入操作。

        通过一遍循环操作完成排序之后，顺序表就被链表化了。

        下面给出一个顺序表被链表化的过程的图示：

       可以很方便的按照访问链表的方式来完成对数据的有序（正序/逆序）遍历访问，但如果是执行查找，不能进行二分查找，只能顺序查找，效率不高，所以还需要把顺序表变成有序表。

        有两种方式来实现这一点。

        第一种，可以new一个空的list，遍历链表，依次把访问到的元素append到list中，最后返回这个list。

       第二种，就地对顺序表重排，实现的逻辑并不复杂，思路是依次取链表的数据元素把它们依次从前往后排在顺序表中，如果它们本身就在应该排的位置什么都不用做，取下一个数据元素继续，如果它们不在应该排的位置上，那么把它们和当前占着该位置的数据元素交换，并且把它们的指针域改成交换出去的数据元素交换到的位置，当后续对被交换出去的数据元素排位的时候，根据它前一结点指针域访问的是它在顺序表中旧（最初）的位置，需要从现在占用它旧位置的数据元素的指针域去取它的当前位置，但有可能在前面的排位过程中它的位置被调换了多次，因此这可能是一个连锁式的查找过程，这个算法的复杂性全在这一点上了。

       下面给出一个顺序表重排变成一个有序表的过程的图示：

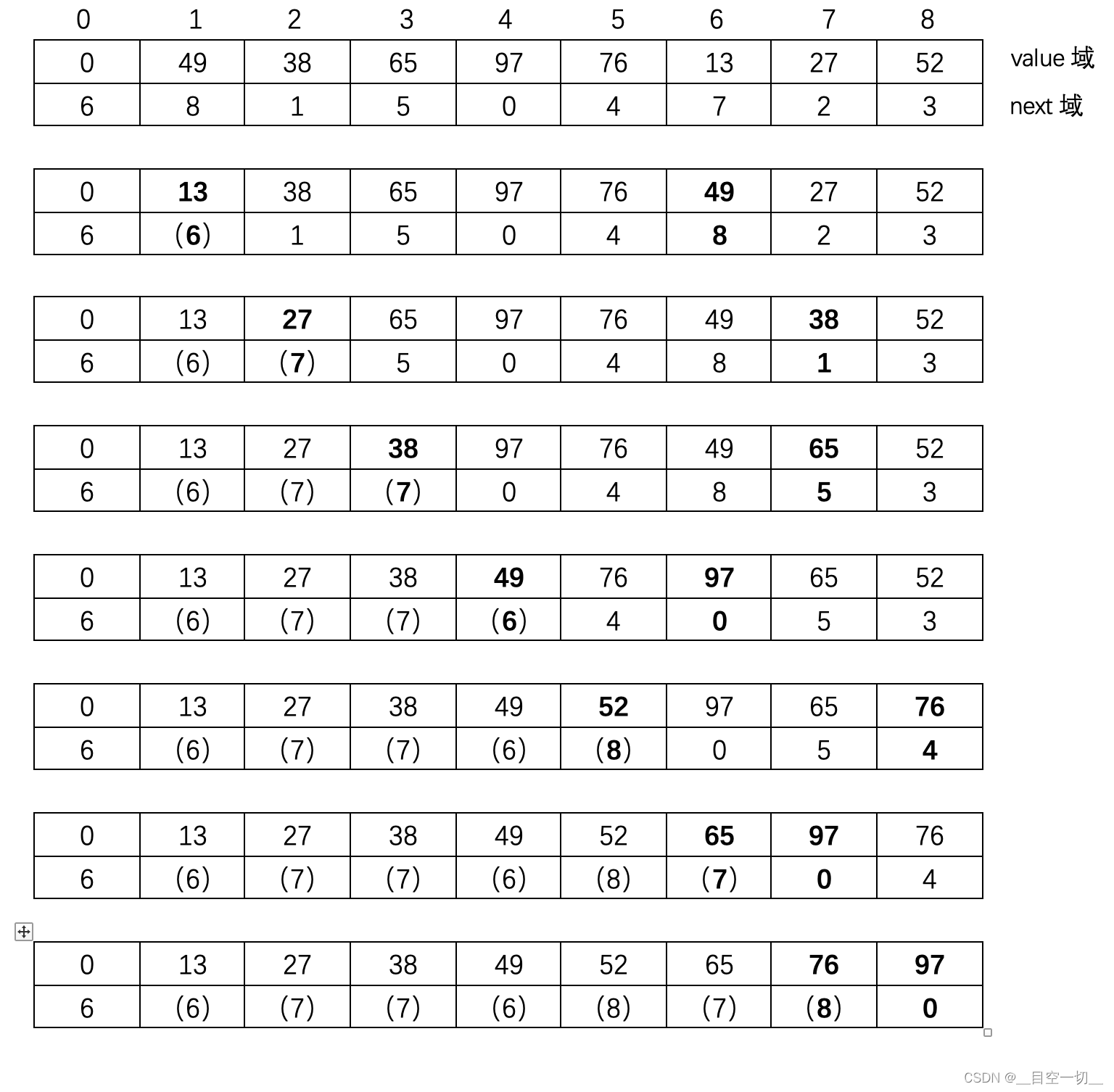
      下面给出代码实现：

def sortwrap(inplace=True):def inner(f):if inplace:def sort(source):source = f(source)next = source[0][1]for i in range(1, len(source)):if i != next:source[i], source[next] = source[next], source[i]next, source[i][1] = source[i][1], nextelse:next = source[i][1]while next <= i and next != 0:next = source[next][1]return sourceelse:def sort(source):source = f(source)pos = source[0][1]result = []while pos != 0:result.append(source[pos][0])pos = source[pos][1]return resultreturn sortreturn inner@sortwrap()
def _insertsort(source):if not source:return source_source = [[0, 0]]_source += [[i, 0] for i in source]head = _source[0]head[1] = 1_source[1][1] = 0for i in range(2, len(_source)):prev = headwhile _source[prev[1]] is not head:if _source[i][0] < _source[prev[1]][0]:_source[i][1] = prev[1]prev[1] = ibreakelse:prev = _source[prev[1]]else:_source[i][1] = prev[1]prev[1] = ireturn _sourceprint(_insertsort((49, 38, 65, 97, 76, 13, 27, 52)))

       这个算法的亮点是实现了顺序表和链表的互转，挺有启发意义的。