LeetCode 239 滑动窗口最大值

本体初始思路是这样的，首先看下给定数组长度和维持一个滑动窗口所需要花费的时间复杂度之间的关系。初步判断是还行的，当然后面被样例打脸了。需要更新成优先队列的解法。原本的解法能通过37/51和46/51的测试用例。但这还不够，面试时候面试官也不会满意的。

原本代码如下：

class Solution {
private:queue<int> myque;// map<int, int> mymap;int quesize = 0;int maxNum = -10000;void quePushPop(int num) {if (num >= maxNum) {int temp = myque.front();myque.pop();myque.push(num);maxNum = num;// mymap[temp]--;// mymap[num]++;} else {if (myque.front() == maxNum) {int temp  = myque.front();myque.pop();myque.push(num);maxNum = -10000;for (int i = 0; i < quesize; i++) {int temp = myque.front();if (maxNum < temp) maxNum = myque.front();myque.pop();myque.push(temp);}// mymap[num++];// mymap[temp]--;// for (auto it = mymap.rbegin(); it != mymap.rend(); it++) {//     if (it->second > 0) {//         maxNum = it->first;//         break;//     }// }} else {int temp = myque.front();myque.pop();myque.push(num);// mymap[temp]--;// mymap[num]++;}}}
public:vector<int> maxSlidingWindow(vector<int>& nums, int k) {quesize = k;vector<int> res;for (int i = 0; i < k; i++) {if (maxNum < nums[i]) maxNum = nums[i];myque.push(nums[i]);// mymap[nums[i]]++;}res.push_back(maxNum);for (int i = k; i < nums.size(); i++) {quePushPop(nums[i]);res.push_back(maxNum);}return res;}
};

使用优先队列的时候其实也蛮简单。首先定义一个pair<int,int>类型的priority_queue即优先队列，之所以要是一个pair类型是因为需要记录存入数据的下标，pair类型就相当于一个两变量结构体，由于是结构体类型，其变量可以直接用first和second访问，还要注意优先队列进行排序时是依据first值来进行的排序，而且是个最大堆（数组实现的完全二叉树）。首先把前k个元素放入优先队列中，之后先把优先队列最顶端的值放入记录答案的int类型vector中，这里完成了对本题中优先队列的初始化。接着开始下标从k到nums.size() - 1的遍历，这个遍历每次先把nums[i]和i组成pair放入优先队列中，再对堆顶元素的下标值进行判断，如果小于i-k，说明不在窗口中，可以直接pop，一直循环直到该元素在窗口范围内，就可以停止并把该值记录入res并进行下一轮循环了。这样一直到结束，就算是完成了题给需求了，当然此时优先队列中还有很多不在窗口中的值，但他们其实不够大到能够影响结果，所以不用去考虑，这也就是优先队列节省的时间之所在——只考虑最大值。

代码如下：

class Solution {
public:vector<int> maxSlidingWindow(vector<int>& nums, int k) {priority_queue<pair<int, int>> mypri_que;vector<int> res;for (int i = 0; i < k; i++) {mypri_que.push(pair(nums[i],i));}    res.push_back(mypri_que.top().first);for (int i = k; i < nums.size(); i++) {mypri_que.push(pair(nums[i],i));while (mypri_que.top().second <= i - k) mypri_que.pop();res.push_back(mypri_que.top().first);}return res;}
};

附注：虽然这是道困难题，但理解了原理之后也还蛮简单的

LeetCode 347 前K个高频元素

这题要求求出nums数组中出现频率前K高的元素，而且我们可以知道这题要用到优先队列，再加上我之前已经有过的一些思考（想到要用map来记录次数），就很简单了。首先定义一个map，记录数组中每个元素出现的次数，时间复杂度O（n）。再像上一题一样定义一个优先队列，在优先队列中我们将map迭代器it指针的second元素作为优先队列节点的first，将it指针的first元素作为优先队列节点的second，这样维护一个最大堆，之后每次从最大堆中取值，并让其出堆，重复K次，就可以得到我们想要的结果了。在这个过程中，前一过程时间复杂度为O（log(n)*log(n)），后一操作时间复杂度为O（k*log(n)）,最大时间复杂度为O(log(n)*log(n))，完美符合条件了。

代码如下：

class Solution {
public:vector<int> topKFrequent(vector<int>& nums, int k) {map<int, int> mymap;priority_queue<pair<int, int>> mypri_que;vector<int> res;for (int i = 0; i < nums.size(); i++) {mymap[nums[i]]++;}for (auto it = mymap.begin(); it != mymap.end(); it++) {mypri_que.push(pair(it->second,it->first));}for (int i = 0; i < k; i++) {res.push_back(mypri_que.top().second);mypri_que.pop();}return res;}
};

之前也说过要补一篇队列的博客，这里就顺便补下吧。首先队列实现起来由于要先入先出，后进的元素又要push到末尾，所以只有一个迭代器来回移动时间复杂度会相当高，所以我们会有两个迭代器，一个是rear作为末尾下标（链式队列中是指针），一个是top作为队首下标（链式队列中是指针）。

顺序数组需要注意的是这是一个从头到尾又到头的数组，即尾下标和头下标分别在入队列和出队列操作时起作用，分别自增，前一个就是正常入队列，在队列尾增加了元素了，后一个就直接将下标后移当成队列中不存在该值，而实际上该内存处如果还没被覆盖，就还是那个值，直到队列再循环一周覆盖它。所以这个队列就完全是一个抽象出来的结构了，实际上它是两个指针构成的一个可以看作窗口的一个结构，不过这个窗口有时候会裂成两半分布在两边。计算大小也是要左右两边分别计算的，rear+1计算0到rear的长度，maxSize（这个是本来就是size + 1了） - front 记录右边的长度。

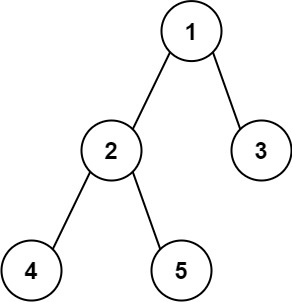
链式队列感觉就很简单了，就如下图所示

这里front就可以看作平时写题目时的虚拟头节点了。

代码如下：