星期一:
dp题单 背包 第四题 混可乐 cf传送门

思路:条件可演化为每种可乐值为 ai-n,选最少的可乐使总和为0(具体可看官方题解
到这会发现背包并不适合了,其实这是道bfs伪装的背包,和牛客周赛39 D很像 牛客传送门
代码如下:
ll n;
int k;
int dis[2020];
void solve(){cin >> n >> k;memset(dis,-1,sizeof dis);queue<int>qu;map<int,int>mp;for(int i=1;i<=k;i++){int x; cin >>x;x=x-n+1000;if(dis[x]==-1) dis[x]=1,qu.push(x),mp[x]=1;}while(!qu.empty()){int t=qu.front(); qu.pop();
// for(int i=0;i<=2000;i++){
// if(i+t-1000<0 || i+t-1000>2000) continue;
// if(dis[t+i-1000]!=-1 || dis[i]!=1) continue;
// dis[t+i-1000]=dis[t]+1;
// qu.push(t+i-1000);
// }for(auto [x,y]:mp){if(x+t-1000<0 || x+t-1000>2000) continue; //x和t都经过了一次偏移if(dis[x+t-1000]!=-1) continue; //所以加起来后需要减一次偏移量dis[x+t-1000]=dis[t]+1; //新到达的点qu.push(x+t-1000);}}if(dis[1000]==-1) cout << "-1\n";else cout << dis[1000] << "\n";
}晚cf,C是dp没出
星期二:
cf edu 165 补C cf传送门

思路:贪心证伪后用dp考虑,状态设计及转移大致如下

这里提一点卡我很久很久的地方,第一重循环 i 需要从0开始枚举
因为状态转移并不是由 i之前推到 i,而是从 i往后面推, i从1开始的话,有些状态无法转移出来,这点在以后也需要注意
代码如下:
const int N=2e6+10,M=210;
const int mod=1e9+7;
ll n;
int k;
int a[N];
ll dp[N][11];
void solve(){cin >> n >> k;for(int i=1;i<=n;i++){cin >> a[i];dp[i][0]=dp[i-1][0]+a[i];for(int j=1;j<=k;j++) dp[i][j]=1e18;}for(int i=0;i<=n;i++){int mi=a[i+1];for(int j=0;j<=k;j++){mi=min(a[i+j+1],mi);for(int o=0;o+j<=k;o++){dp[i+j+1][o+j]=min(dp[i][o]+1ll*mi*(j+1),dp[i+j+1][o+j]);}}}cout << dp[n][k] << "\n";
}晚cf round942 div2,最后十分钟出C,又被permutation拿下了
星期三:
上午vp牛客周赛28
E 牛客传送门
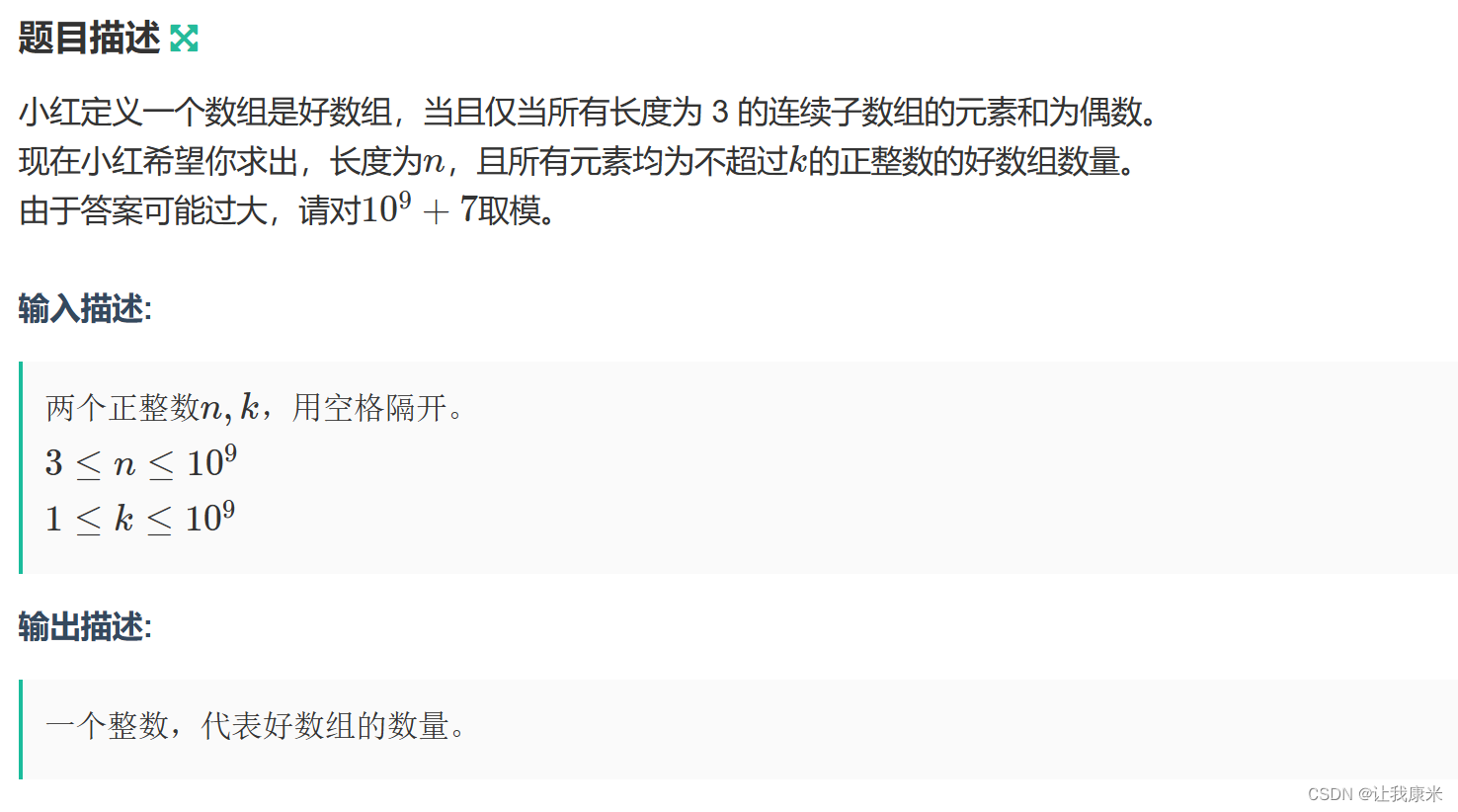
思路:三个连续数的和为偶数,组合形式有限,分别为偶偶偶,偶奇奇,奇偶奇,奇奇偶,数组最先三个数的奇偶性确定后,整个数组的每个数的奇偶性都确定了
算出k以内的数能选的奇数和偶数个数,n个位置中奇数和偶数各有多少个,乘法原理和快速幂计算
代码如下:
const int mod=1e9+7;
ll n;
ll k;
ll qpow(int a,int n){if(n==0) return 1;if(n==1) return a;ll s=qpow(a,n/2);s=s*s%mod;if(n&1) s=s*a%mod;return s;
}
void solve(){cin >> n >> k;int num0=0,num1=0;num0=k/2,num1=k/2+(k&1);ll ans=qpow(num0,n); //全偶int n0=n/3,n1=n/3*2;if(n%3==0) ans+=3*qpow(num1,n1)*qpow(num0,n0)%mod,ans%=mod;if(n%3==1)ans+=2*qpow(num1,n1+1)*qpow(num0,n0)%mod,ans+=qpow(num1,n1)*qpow(num0,n0+1),ans%=mod;if(n%3==2)ans+=2*qpow(num1,n1+1)*qpow(num0,n0+1)%mod,ans+=qpow(num1,n1+2)*qpow(num0,n0),ans%=mod;cout << ans;
}下午牛客五一 1,很难,看情况补题
周赛28 F题离散化+树状数组,先复习下树状数组,刚好趁五一假期学点数据结构
洛谷树状数组板子题其一(单点修改,区间查询 洛谷传送门

代码如下:
const int N=2e6+10,M=210;
const int mod=1e9+7;
ll n;
ll m;
ll a[N];
ll t[N];
int lowbit(int x){return x&-x;}
void ad(int x,int v){for(int i=x;i<=n;i+=lowbit(i)) t[i]+=v;
}
ll ask(int x){ll res=0;for(int i=x;i;i-=lowbit(i)) res+=t[i];return res;
}
void solve(){cin >> n >> m;for(int i=1;i<=n;i++){cin >> a[i];ad(i,a[i]); //nlogn构造树状数组}while(m--){int op,x,y; cin >> op >> x >> y;if(op==1) ad(x,y);else cout << ask(y)-ask(x-1) << "\n";}
}树状数组板子题其二(区间修改,单点查询 洛谷传送门
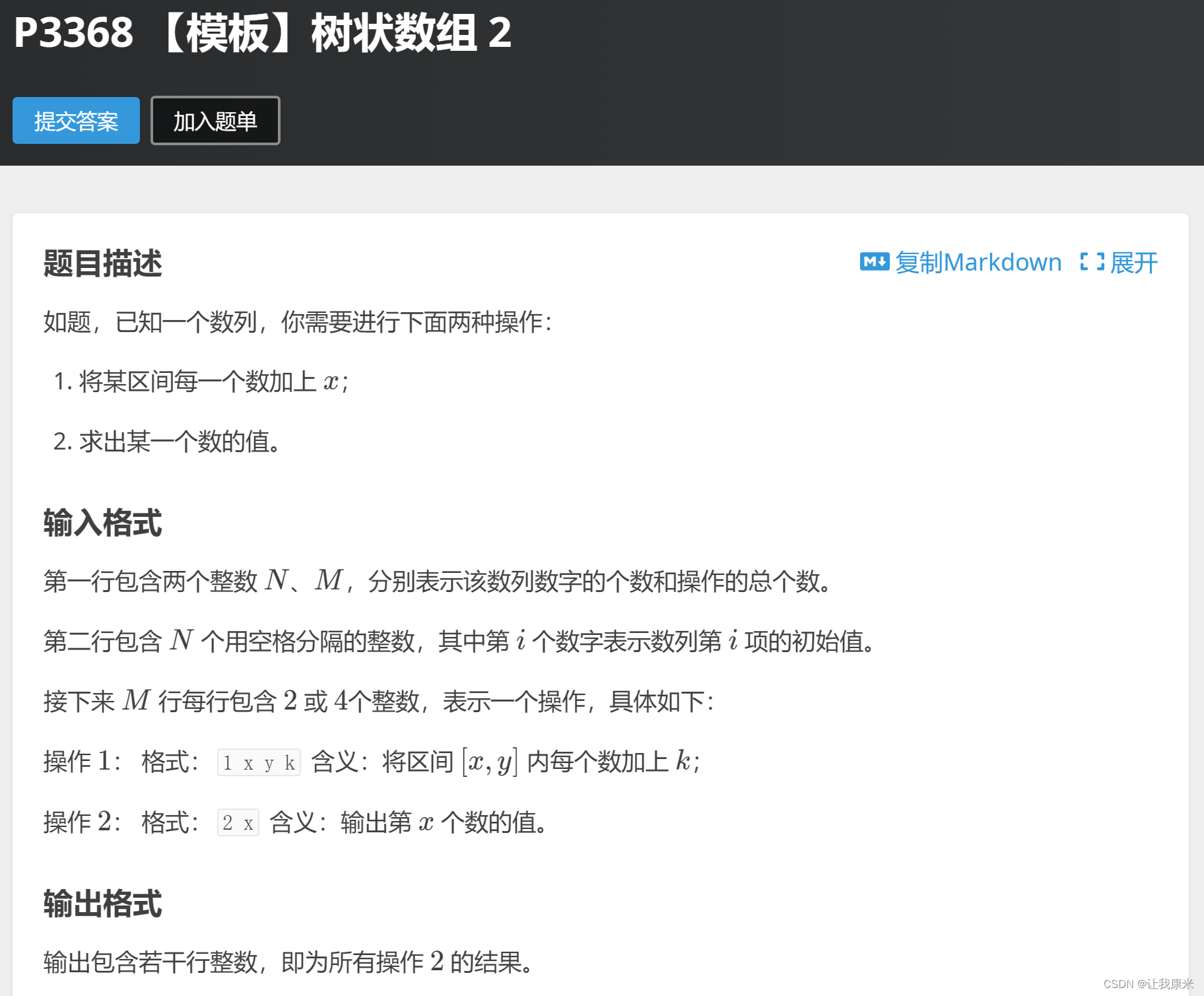
代码如下:
const int N=2e6+10,M=210;
const int mod=1e9+7;
ll n;
ll m;
ll a[N];
ll t[N];
int lowbit(int x){return x&-x;}
void ad(int x,int v){for(int i=x;i<=n;i+=lowbit(i)) t[i]+=v;
}
ll ask(int x){ll res=0;for(int i=x;i;i-=lowbit(i)) res+=t[i];return res;
}
void solve(){cin >> n >> m;for(int i=1;i<=n;i++) cin >> a[i];while(m--){int op,x; cin >> op >> x;if(op==1){int y,k; cin >> y >> k;ad(x,k); ad(y+1,-k); //差分思想,x到y这段区间加上了k}else cout << a[x]+ask(x) << "\n"; //t数组维护的是修改值}
}星期四:
补牛客周赛28 F 牛客传送门

思路:因为前缀和不再有单调性,所以easy版本二分和双指针的做法失效,用离散化+树状数组
区间元素和大于等于k,即 a【l-1】<= a【r】- k,我们可以枚举右端点,然后查询有多少个左端点小于等于这个值,枚举后将此右端点加入左端点的集合,这里用权值树状数组来实现
权值树状数组,单点修改,区间查询,修改的意义是值为x的数多了1,查询的意义即为<= x的值个数,类似于用树状数组维护桶数组
不过由于值的范围能到达1e14,需要离散化处理,即按照原值的大小关系映射为紧密连续的值,这里需要用到的值不仅有 a【i】,还有 a【i】- k 用于查询,所以离散化后数据范围最多 2e5
最后一个需要注意的点是,add函数的 i <= n,需改为 i <= 离散化后映射的最大值,因为这才是 离散化后权值树的最大下标
代码如下:
const int N=2e6+10,M=210;
const int mod=1e9+7;
ll n;
ll a[N],k;
ll t[N],cnt;
map<ll,int>to;
int lowbit(int x){return x&-x;}
void add(int x,int v){for(int i=x;i<=cnt;i+=lowbit(i)) t[i]+=v; //注意下标并不为 n !!!
}
ll ask(int x){ll res=0;for(int i=x;i;i-=lowbit(i)) res+=t[i];return res;
}
void solve(){cin >> n >> k;for(int i=1;i<=n;i++){cin >> a[i];a[i]+=a[i-1];to[a[i]]=1,to[a[i]-k]=1;}to[0]=1;for(auto &[x,y]:to) y=++cnt; //离散化处理ll ans=0;add(to[0],1); //因为查询的是a[l-1],a[0]=0的值先加上for(int i=1;i<=n;i++){ans+=ask(to[a[i]-k]); //查询add(to[a[i]],1); //权值+1}cout << ans;
}牛客五一集训 1 补B(斐波那契字符串 牛客传送门

思路:n 比较小,可以递归求解,f 数组储存此字符串的长度
代码如下:
ll n;
ll f[550];
const ll MA=1e12+10;
inline char fnd(int n,ll k){if(n==1) return "COFFEE"[k-1];if(n==2) return "CHICKEN"[k-1];if(k<=f[n-2]) return fnd(n-2,k); //此字符属于第i-2个字符串else return fnd(n-1,k-f[n-2]); //否则属于第i-1个
}
void solve(){f[1]=6,f[2]=7;for(int i=3;i<=510;i++) f[i]=min(MA,f[i-2]+f[i-1]);int t; cin >> t;while(t--){ll k; cin >> n >> k;for(ll i=k;i<min(k+10,f[n]+1);i++) cout << fnd(n,i);//i注意开llcout << "\n";}
}其他题都不是很好补,先放会
准备补牛客寒假集训营2的两道线段树题,过程可能会比较漫长,期望在4号内完成
晚cf round 943,B题翻车,题数4题
星期五:
先敲个线段树板子,复习下
代码如下:(区间修改,区间查询
const int N=2e6+10,M=210;
const int mod=1e9+7;
ll n;
#define lc p<<1
#define rc p<<1|1
int m;
struct nod{ll l,r,sum,add; //左端点,右端点,区间总和,懒标记
}t[N]; //要开原数组 4倍大小
ll a[N];
void pushup(int p){ //向上更新t[p].sum=t[lc].sum+t[rc].sum;
}
void pushdn(int p){ //向下更新if(!t[p].add) return ;t[lc].sum+=(t[lc].r-t[lc].l+1)*t[p].add;t[rc].sum+=(t[rc].r-t[rc].l+1)*t[p].add;t[lc].add+=t[p].add;t[rc].add+=t[p].add;t[p].add=0;
}
void bd(int p,int l,int r){t[p]={l,r,a[l],0};if(l==r) return ; //叶子节点int m=l+r>>1;bd(lc,l,m);bd(rc,m+1,r);pushup(p);
}
ll ask(int p,int x,int y){ //区间查询if(x<=t[p].l && y>=t[p].r) return t[p].sum; //被查询区间完全覆盖,则直接返回sumll sum=0;int m=t[p].l+t[p].r>>1;pushdn(p); //向下查前先向下更新if(x<=m) sum+=ask(lc,x,y); //有覆盖到左子节点if(y>m) sum+=ask(rc,x,y); //有覆盖到右子节点return sum;
}
void updt(int p,int x,int y,int k){if(x<=t[p].l && y>=t[p].r){t[p].sum+=(t[p].r-t[p].l+1)*k;t[p].add+=k;return ; //打上懒标记,直接返回}int m=t[p].l+t[p].r>>1;pushdn(p); //记得先向下更新if(x<=m) updt(lc,x,y,k);if(y>m) updt(rc,x,y,k);pushup(p); //再向上更新
}
void solve(){cin >> n >> m;for(int i=1;i<=n;i++) cin >> a[i];bd(1,1,n);while(m--){int op,x,y; cin >> op >> x >> y;if(op==1){int k; cin >> k;updt(1,x,y,k);}else cout << ask(1,x,y) << "\n";}
}补牛客寒假营2 G 牛客传送门

思路:线段树维护两个信息,区间最大值( suma【i】- 2*a【i】) 和区间和,但区间和不需要区间修改,区间最大值需要(a【x】变化会使 x到n的前缀和改变),所以一个懒标记给区间最大值用就行
官方题解:【题解】2024牛客寒假算法基础集训营2_牛客网 (nowcoder.com)
还有一个我de了半个下午,需要注意的一点是,求区间信息时,一定要确保 l <= r !!!
代码如下:(魔改的比较随意
const int N=2e6+10,M=210;
const int mod=1e9+7;
ll n;
#define lc p<<1
#define rc p<<1|1
struct nod{ll l,r,sum,add,ma;
}t[N];
ll a[N],suma[N];
void pushup(int p){t[p].sum=t[lc].sum+t[rc].sum;t[p].ma=max(t[lc].ma,t[rc].ma);
}
void pushdn(int p){if(!t[p].add) return ;t[lc].ma+=t[p].add; //懒标记只需给最大值用t[rc].ma+=t[p].add;t[lc].add+=t[p].add;t[rc].add+=t[p].add;t[p].add=0;
}
void bd(int p,int l,int r){t[p]={l,r,a[l],0,suma[l]-2*a[l]};if(l==r) return ;int m=l+r>>1;bd(lc,l,m);bd(rc,m+1,r);pushup(p);
}
ll ask(int p,int x,int y,int op){ //op为1求区间和,为2求区间最大值if(x<=t[p].l && y>=t[p].r){if(op==1) return t[p].sum;else return t[p].ma;}ll res=0;int m=t[p].l+t[p].r>>1;pushdn(p); //记得向下更新if(op==1){res=0;if(x<=m) res+=ask(lc,x,y,1);if(y>m) res+=ask(rc,x,y,1);}else{res=-1e18;if(x<=m) res=max(ask(lc,x,y,2),res);if(y>m) res=max(ask(rc,x,y,2),res);}return res;
}
void updt(int p,int x,int y,int k,int op){ //op为1改区间最大值,为2改区间和(单点修改)if(x<=t[p].l && y>=t[p].r){if(op==1){t[p].ma+=k;t[p].add+=k;}else t[p].sum=k;return ;}int m=t[p].l+t[p].r>>1;pushdn(p);if(x<=m) updt(lc,x,y,k,op);if(y>m) updt(rc,x,y,k,op);pushup(p);
}
void solve(){int q; cin >> n >> q;for(int i=1;i<=n;i++){cin >> a[i];suma[i]=suma[i-1]+a[i];}bd(1,1,n);while(q--){int op,x,y; cin >> op >> x >> y;if(op==1){updt(1,x,x,2*a[x]-2*y,1); //将 sum[i]-2*a[x]改为 sum[i]-2*yupdt(1,x,n,y-a[x],1); //x-n的区间最大值全减a[x]加y (前缀和改变)updt(1,x,x,y,2);a[x]=y;}else{
// cout << ask(1,x+1,y,2)-ask(1,1,x-1,1) << "\n";ll res=ask(1,x+1,y,2);if(x-1>=1) res-=ask(1,1,x-1,1); // 特判x-1!!!cout << res << "\n";}}
}星期六:
线段树维护区间最大子段和板子题 洛谷传送门
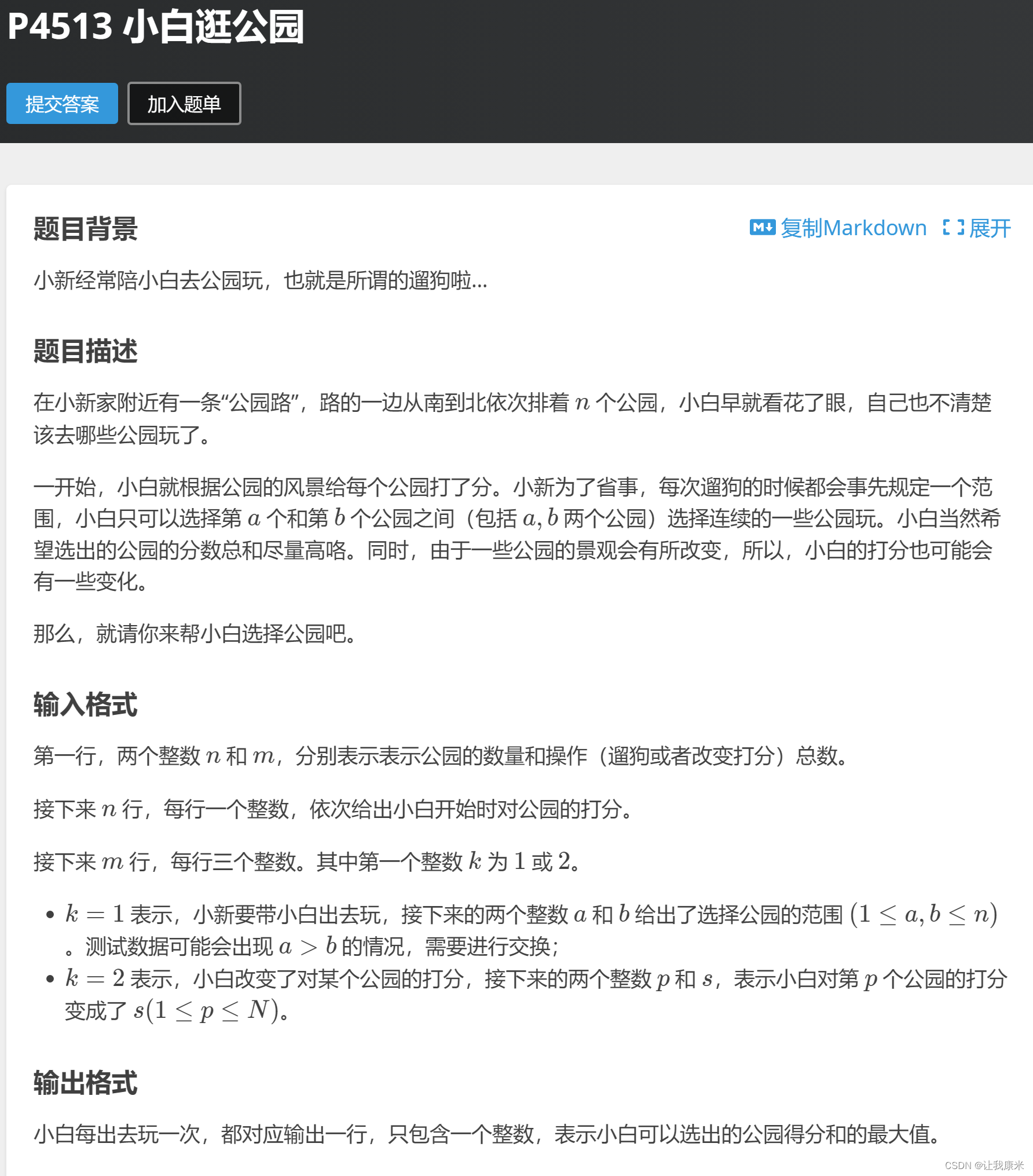
代码如下:
const int N=2e6+10,M=210;
const int mod=1e9+7;
ll n;
struct seg_Tree{#define lc p<<1#define rc p<<1|1struct nod{int l,r;ll sum,maxl,maxr,ma;}t[N];int ql,qr; //查询区间nod merge(nod a,nod b){nod res;res.l=a.l,res.r=b.r;res.sum=a.sum+b.sum;;res.maxl=max(a.maxl,a.sum+b.maxl);res.maxr=max(b.maxr,a.maxr+b.sum);res.ma=max({a.maxr+b.maxl,a.ma,b.ma});return res;}void pushup(int p){t[p]=merge(t[lc],t[rc]);} //向上更新void bd(int p,int l,int r){ //bd里处理输入if(l==r){t[p]={l,r,0,-0x3f3f3f3f,-0x3f3f3f3f,-0x3f3f3f3f};cin >> t[p].sum;t[p].maxl=t[p].maxr=t[p].ma=t[p].sum;return ;}int m=l+r>>1;bd(lc,l,m);bd(rc,m+1,r);pushup(p);}void update(int p,int v){if(ql<=t[p].l && qr>=t[p].r){t[p].sum=t[p].maxl=t[p].maxr=t[p].ma=v; //叶子节点的所有信息都要改return ;}int m=t[p].l+t[p].r>>1;if(ql<=m) update(lc,v);if(qr>m) update(rc,v);pushup(p); //向上更新}nod query(int p){if(ql<=t[p].l && qr>=t[p].r) return t[p];int m=t[p].l+t[p].r>>1;if(ql>m) return query(rc);if(qr<=m) return query(lc);return merge(query(lc),query(rc));}void updt(int l,int r,int v){ql=l;qr=r;
// qop=op;update(1,v);}ll ask(int l,int r){ql=l,qr=r;return query(1).ma;}#undef lc#undef rc
}tr;
void solve(){int m; cin >> n >> m;tr.bd(1,1,n);while(m--){int k,a,b; cin >> k >> a >> b;if(k==1){if(a>b) swap(a,b);cout << tr.ask(a,b) << "\n";}else tr.updt(a,a,b);}
}周日:
川大校赛初赛,输
补牛客寒假营2 H 牛客传送门
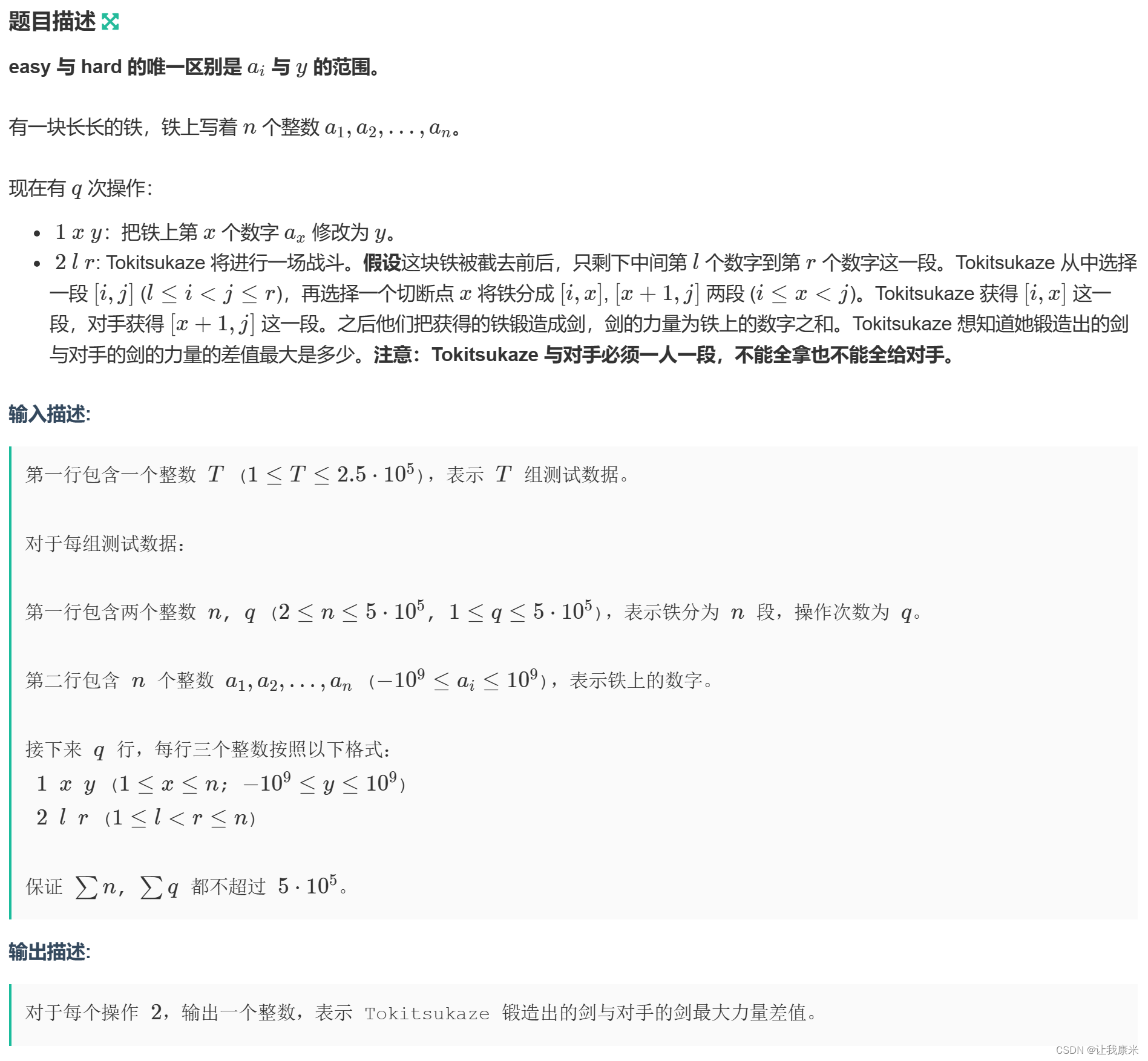
思路:easy版本的贪心失效,在线段树维护区间最大子段和的基础上修改一下
官方题解很详细:【题解】2024牛客寒假算法基础集训营2_牛客网 (nowcoder.com)
代码如下:
const int N=2e6+10,M=210;
const ll INF=0x3f3f3f3f3f3f3f3f; //必须得开ll
const int mod=1e9+7;
ll n;
struct seg_Tree{#define lc p<<1#define rc p<<1|1struct nod{int l,r;ll sum,maxr,minl,ansl,ansr,segans,ans;}t[N];int ql,qr,qop,a[N];nod merge(nod a,nod b){nod res;res.l=a.l,res.r=b.r;res.sum=a.sum+b.sum;res.maxr=max(b.maxr,a.maxr+b.sum);res.minl=min(a.minl,a.sum+b.minl);res.ansl=max({a.ansl,a.sum+b.ansl,a.sum-b.minl,a.segans-b.minl});res.ansr=max({b.ansr,a.ansr-b.sum,a.maxr-b.sum,a.maxr+b.segans});res.segans=max({a.sum-b.sum,a.segans-b.sum,a.sum+b.segans});res.ans=max({a.ans,b.ans,a.maxr-b.minl,a.ansr-b.minl,a.maxr+b.ansl});return res;}void pushup(int p){t[p]=merge(t[lc],t[rc]);}void bd(int p,int l,int r){t[p]={l,r,a[l],-INF,INF,-INF,-INF,-INF,-INF};if(l==r){t[p].maxr=t[p].minl=t[p].sum;return ;}int m=l+r>>1;bd(lc,l,m);bd(rc,m+1,r);pushup(p);}void update(int p,int v){if(ql<=t[p].l && qr>=t[p].r){t[p].maxr=t[p].minl=t[p].sum=v;return ;}int m=t[p].l+t[p].r>>1;if(ql<=m) update(lc,v);if(qr>m) update(rc,v);pushup(p);}nod query(int p){if(ql<=t[p].l && qr>=t[p].r) return t[p];int m=t[p].l+t[p].r>>1;if(ql>m) return query(rc);if(qr<=m) return query(lc);return merge(query(lc),query(rc));}void updt(int l,int r,int v){ql=l;qr=r;
// qop=op;update(1,v);}ll ask(int l,int r){ql=l,qr=r;return query(1).ans;}#undef lc#undef rc
}tr;
void solve(){int q; cin >> n >> q;for(int i=1;i<=n;i++) cin >> tr.a[i];tr.bd(1,1,n);while(q--){int op,x,y; cin >> op >> x >> y;if(op==1) tr.updt(x,x,y);else cout << tr.ask(x,y) << "\n";}
}![[C++][数据结构]二叉搜索树:介绍和实现](https://img-blog.csdnimg.cn/direct/6f3eecc7fa6f472db3e13b17244bffa3.png)




![[C++基础学习-06]----C++指针详解](https://img-blog.csdnimg.cn/direct/ba7d3d958bb0454794ba1e37da3ef71f.png)